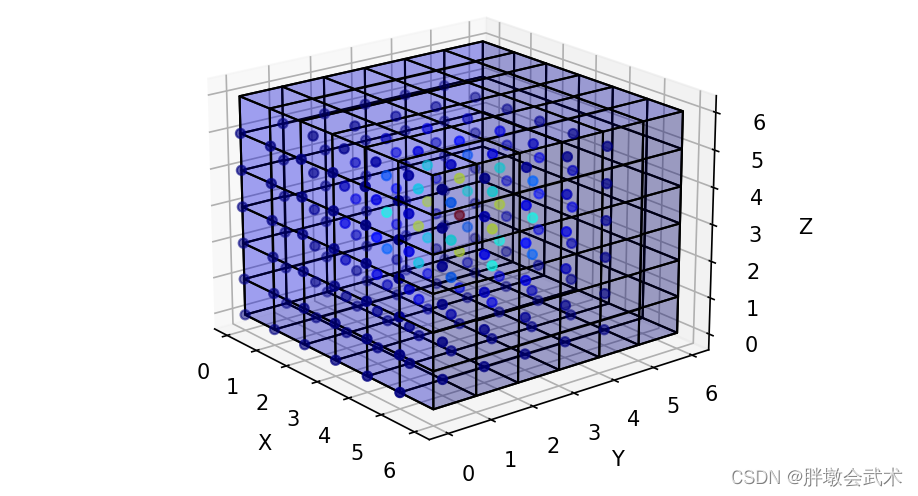
算法说明：
（1）首先定义一个中心点坐标 center，标准差 sigma 和峰值 amplitude。
（2）然后通过计算每个点到中心点的欧氏距离，并将欧氏距离应用于高斯分布的公式 amplitude * exp(-distances**2 / (2 * sigma**2))，得到立方体的值 cube。

（说明1）高斯分布是一个连续的概率分布，具有峰值中心和标准差控制的形状。
（说明2）在这里，立方体的数值表示每个点在高斯分布上的概率密度，而不是完全符合连续高斯分布。
（说明3）由于离散化的限制，立方体的表现是一个近似的离散高斯分布。
（说明4）所以虽然不是完全连续的高斯分布，但在给定的离散空间中，它可以近似地表示高斯分布的特性，如中心峰值和逐渐减小的分布。

import matplotlib.pyplot as plt
import numpy as np
import torch


def generate_gaussian_cube(size, center, sigma, amplitude):
    # 创建网格点坐标
    indices = np.indices(size)
    coordinates = torch.tensor(indices, dtype=torch.float32)
    center = center.view(3, 1, 1, 1)  # 扩展 center 的维度
    # 计算每个点到中心点的欧氏距离
    distances = torch.sqrt(torch.sum((coordinates - center)**2, dim=0))
    # 根据高斯分布计算立方体的值
    cube = amplitude * torch.exp(-distances**2 / (2 * sigma**2))
    return cube


# （1）创建高斯分布的立方体
size_l = 6
center_l = 3
size = (size_l, size_l, size_l)                             # 立方体尺寸
center = torch.tensor([center_l, center_l, center_l])       # 中心点坐标
sigma = 1.0             # 标准差
amplitude = 255.0       # 峰值
cube = generate_gaussian_cube(size, center, sigma, amplitude)

# （2）打印参数
average_gray_value = torch.mean(cube)
print(cube.min(), cube.max())
print("Average Gray Value:", average_gray_value.item())

# （3）创建3D坐标轴
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# （4）绘制立方体
ax.voxels(cube.numpy(), facecolors='b', edgecolor='k', alpha=0.2)

# （5）绘制3D散点图
# 获取非零坐标和对应的值
indices = torch.nonzero(cube)
x_vals = indices[:, 0].numpy()
y_vals = indices[:, 1].numpy()
z_vals = indices[:, 2].numpy()
cube_vals = cube[indices[:, 0], indices[:, 1], indices[:, 2]].numpy()
ax.scatter(x_vals, y_vals, z_vals, c=cube_vals, cmap='jet')

ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()