文章目录
- 一、机器学习是什么?
- 二、模型训练
- YouTube流量预测
- 1. 先写一个具有未知参数的函数(Function)
- 2. 定义损失(从训练数据进行计算)
- 3.最优化
- 4.结果分析
- Back to framework
- 1.带有未知数的函数:
- 2.定义损失(从训练数据进行计算)
- 3. 最优化
- 4.激活函数
- 5.继续改我们的模型
- 三、Neural Network
一、机器学习是什么?
机器学习≈找一个函数
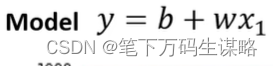
这个函数不是人能容易的找出来,需要借助机器的力量。

不同的函数:
- 回归(Regression):函数输出一个标量。eg.对PM2.5的预测:
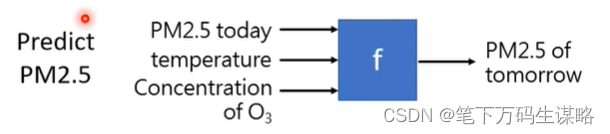
- 分类(Classification):给定选项(类),函数输出正确的选项。eg1二分类.是否为垃圾邮件:

eg2多分类.下围棋:
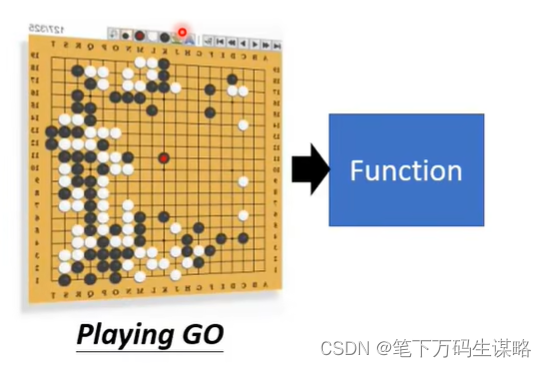
二、模型训练
训练:
- 先写一个具有未知参数的函数(Function)
- 定义损失(从训练数据进行计算)
- 最优化
YouTube流量预测
有没有可能找一个函数,输入是这个频道后台的数据,输出隔天的总点阅率?
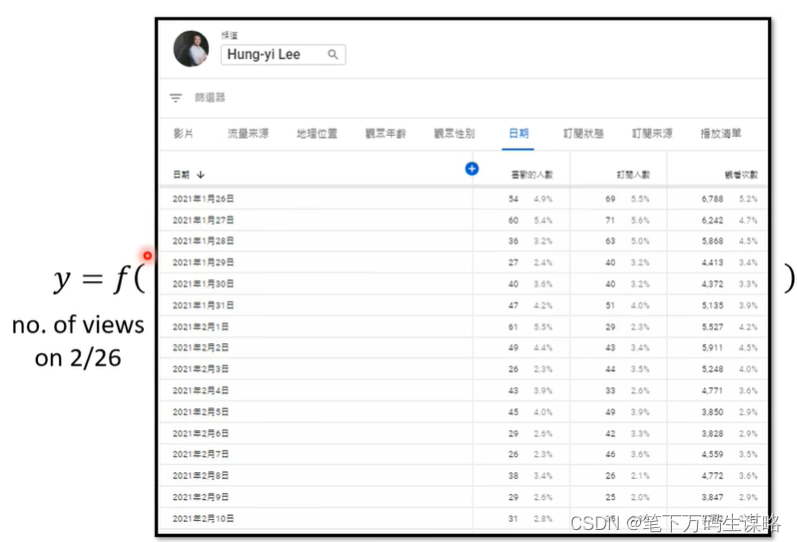
机器学习找这个函数分为三个过程,以 YouTube流量预测为例。
1. 先写一个具有未知参数的函数(Function)
先猜测函数的类型

2. 定义损失(从训练数据进行计算)
损失是一个关于参数的函数

函数输入的值代表:这一组参数设定某一组数值,这个数值是好还是不好。
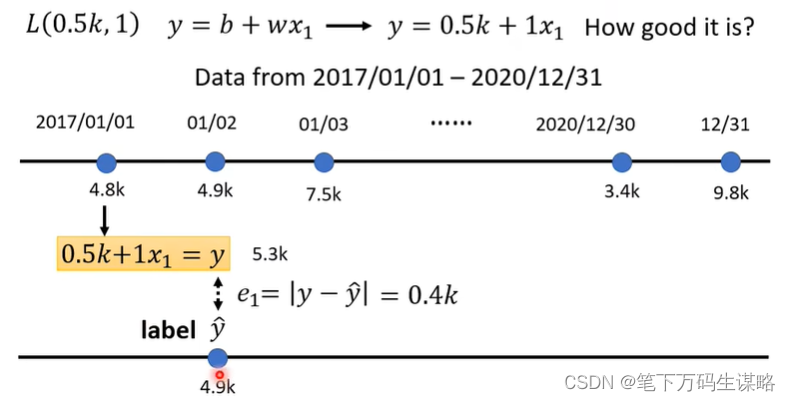
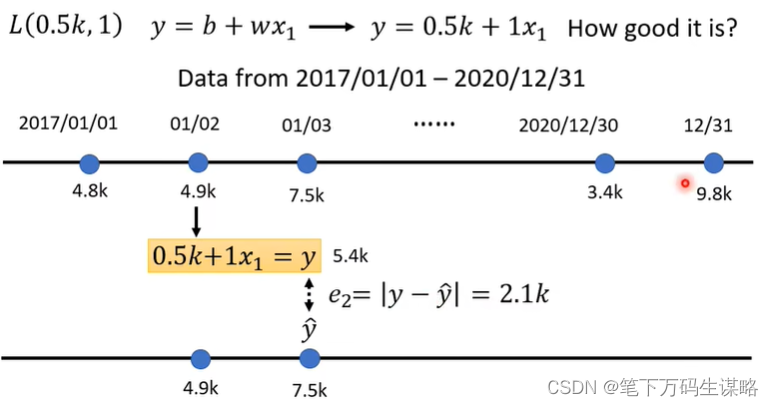
同样的方法,我们可以算出三年来每一天的预测误差。
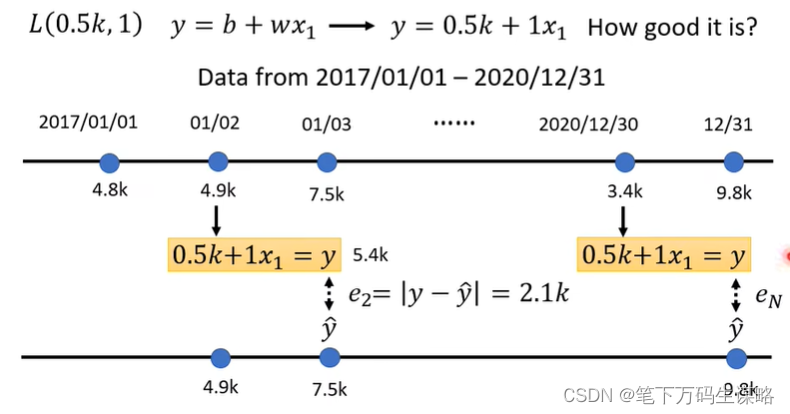
接下来我们把三年的误差求平均。
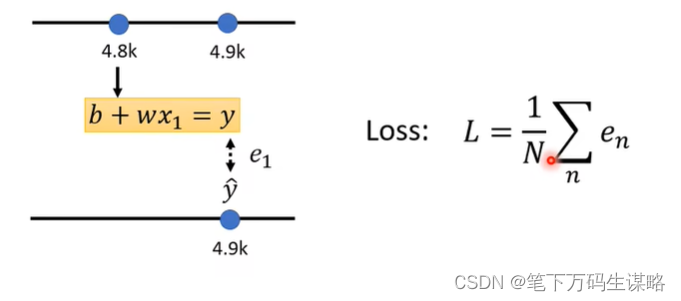
L越小参数设置越好,越大越不好。
计算误差有很多方式,根据需求选取。

如果真实值与预测值是概率分布,可能选择交叉熵损失。
误差曲面:
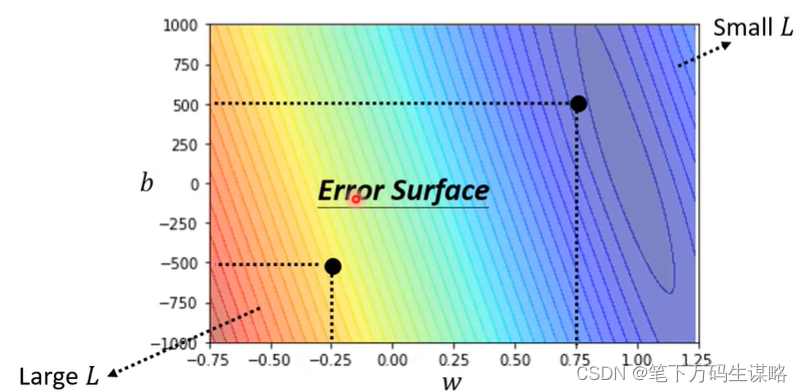
3.最优化
找一组参数是的L最小

为此我们使用梯度下降(gradient decent)
简化过程,一个参数的gradient decent:

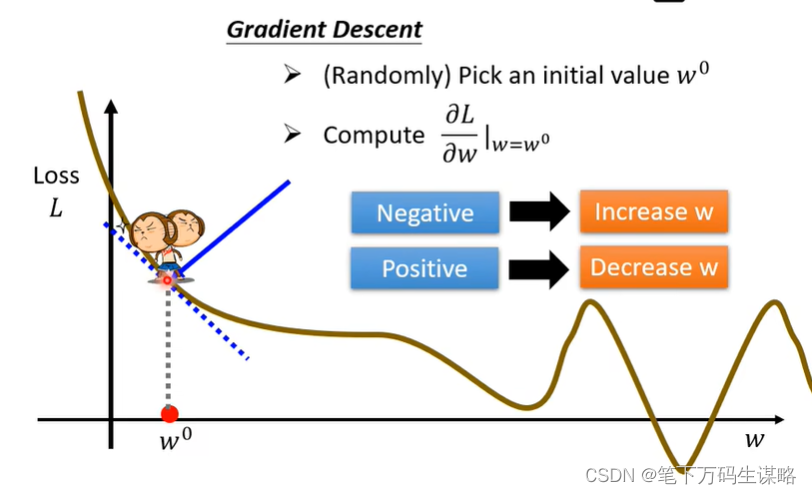
- 随机选取初始点 w 0 w_0 w0
- 计算
∂
L
∂
w
∣
w
=
w
0
\frac{\partial L}{\partial w}|_{w=w_0}
∂w∂L∣w=w0。(就是看左右哪边高,向低的跨步)
若求出为负值(左高右低的切线),增大w,loss就变小;若求出为正值(左低右高的切线),减小w,loss就变大。
步子跨多大,取决于:1.斜率(斜率大就跨大一点),2学习率(自己设定的) - 更新迭代w
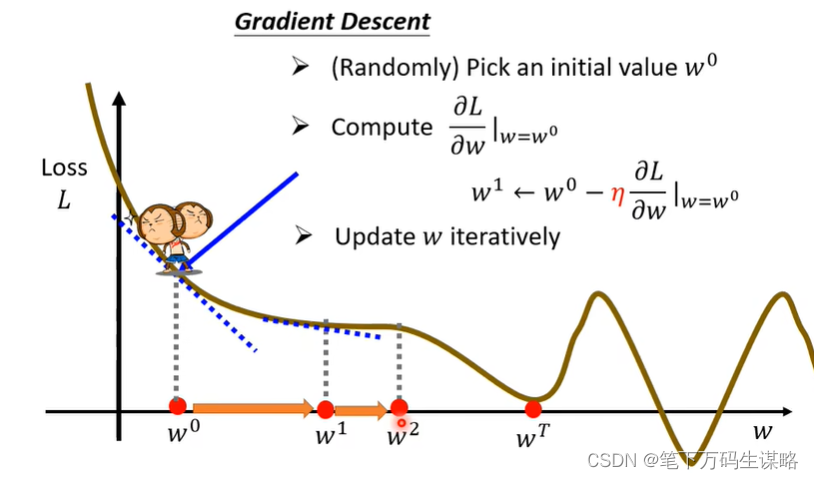
当 ∂ L ∂ w ∣ w = w 0 \frac{\partial L}{\partial w}|_{w=w_0} ∂w∂L∣w=w0计算为0就不在更新了。
有可能梯度下降会陷入局部最优
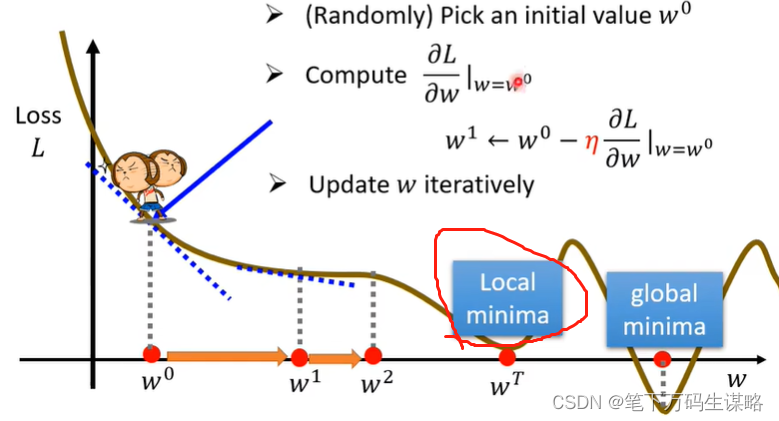
局部最小值真的会导致问题吗?(后面会说gradient decent的真正痛点)
两个参数的gradient decent:
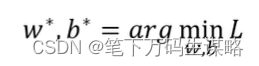
- 随机选取初始点 w 0 , b 0 w_0,b_0 w0,b0
- 计算
∂
L
∂
w
∣
w
=
w
0
,
b
=
b
0
,
∂
L
∂
b
∣
w
=
w
0
,
b
=
b
0
\frac{\partial L}{\partial w}|_{w=w_0,b=b_0},\frac{\partial L}{\partial b}|_{w=w_0, b=b_0}
∂w∂L∣w=w0,b=b0,∂b∂L∣w=w0,b=b0。(就是看左右哪边高,向低的跨步)
若求出为负值(左高右低的切线),增大w,loss就变小;若求出为正值(左低右高的切线),减小w,loss就变大。
步子跨多大,取决于:1.斜率(斜率大就跨大一点),2学习率(自己设定的) - 更新迭代w

在深度学习中,微分应该怎么算? ---- 程序会自己算

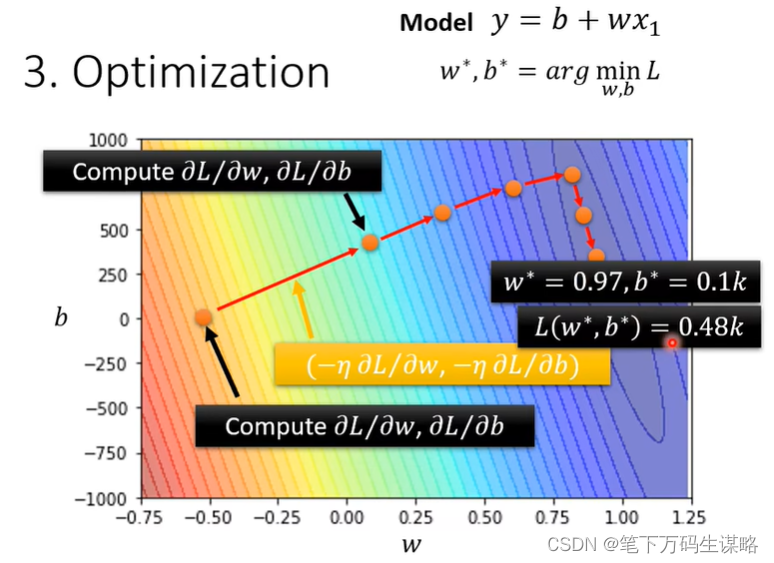
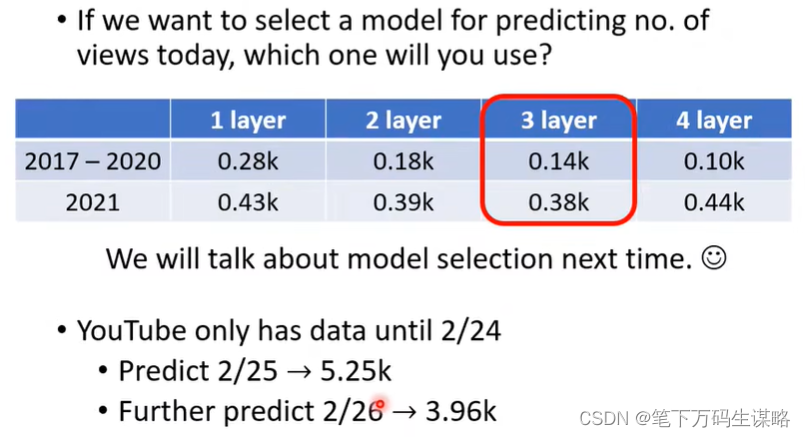
4.结果分析

能否做的更好?
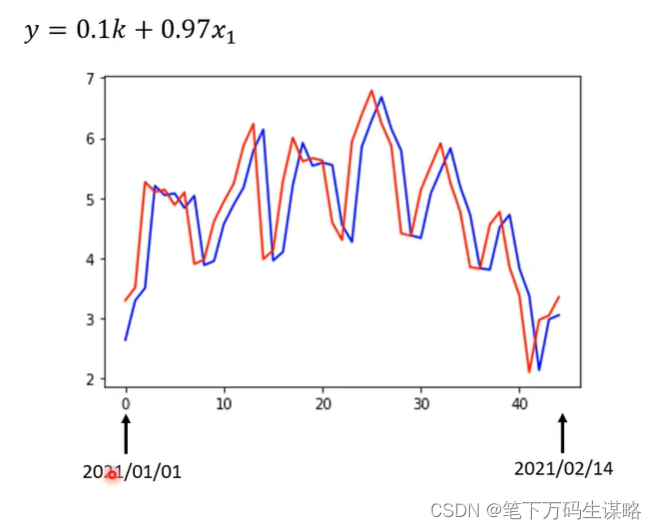
从图中看出,7天一个循环。我们分别考虑2017-2020的前1、7、18、56天,对2021年的某一天的影响。我们采用的是Linear Model。

线性模型太简单了… 我们需要更复杂的模式。
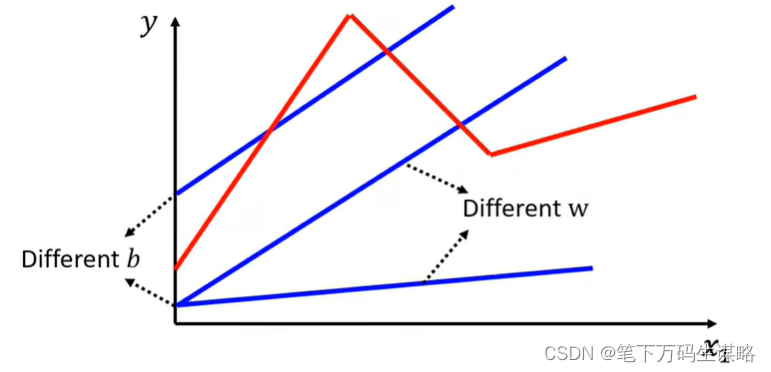
线性模型具有严重的局限性。模型偏差我们需要一个更灵活的模式!
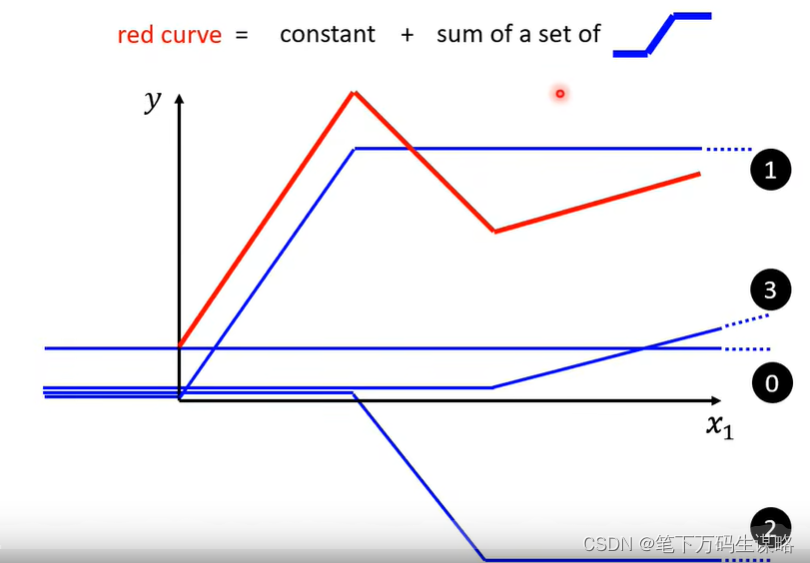
所有分段的线性曲线可以可以由常数与一系列蓝色Function组成。
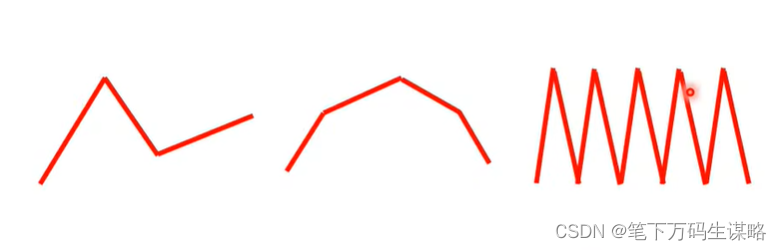
转折越多,越复杂,需要的蓝色Function就越多。
如果不是分段曲线,而是连续曲线,我们可以使用分段线性曲线去逼近。
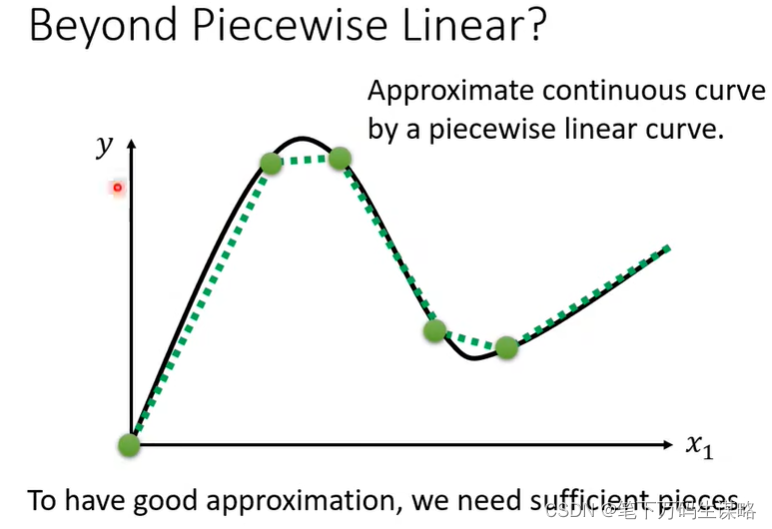
如何表示蓝色的Function呢?
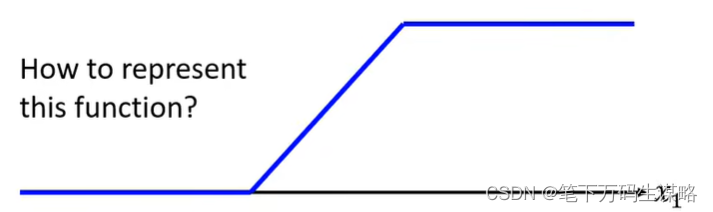
我们可以使用
y
=
c
1
1
+
e
−
(
b
+
w
1
x
)
y=c\frac{1}{1+e^{-(b+w_1x)}}
y=c1+e−(b+w1x)1:
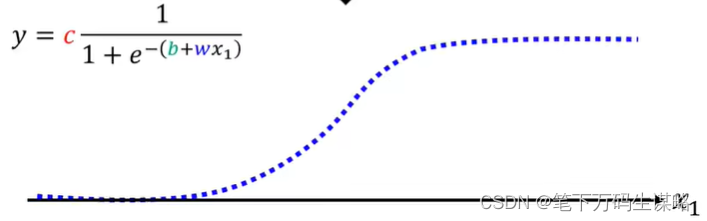
Sigmoid Function(S型曲线):
y
=
c
∗
s
i
g
m
o
i
d
(
b
+
w
1
x
)
=
c
1
1
+
e
−
(
b
+
w
1
x
)
y = c*sigmoid(b+w_1x) = c\frac{1}{1+e^{-(b+w_1x)}}
y=c∗sigmoid(b+w1x)=c1+e−(b+w1x)1
w改变斜率、b曲线左右移动、c改变他的高度:
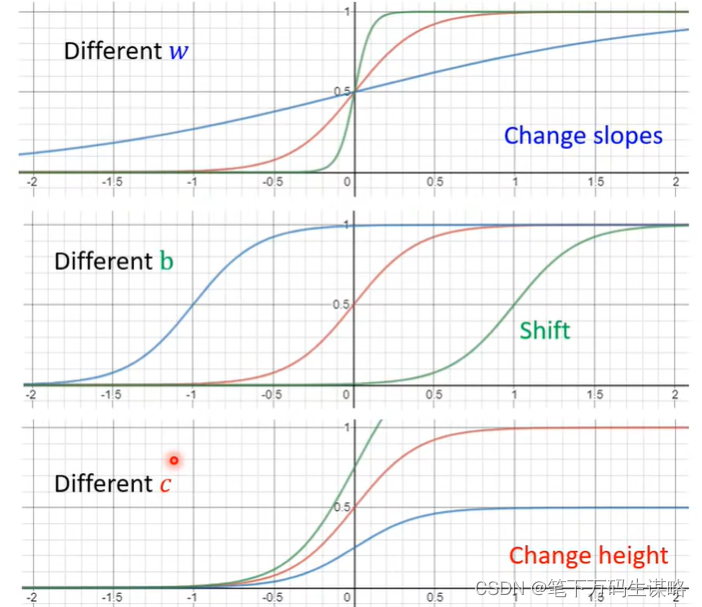
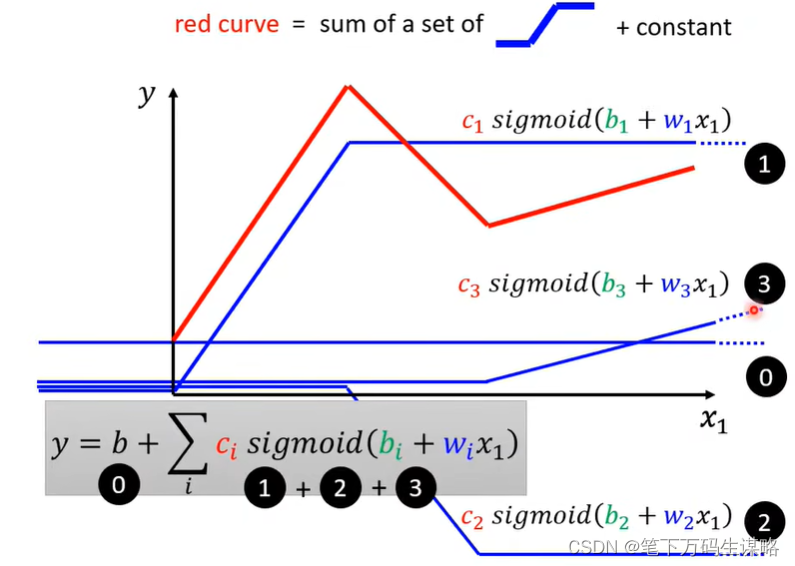
新的模型:有更多的特征

我们把它画出来,直观
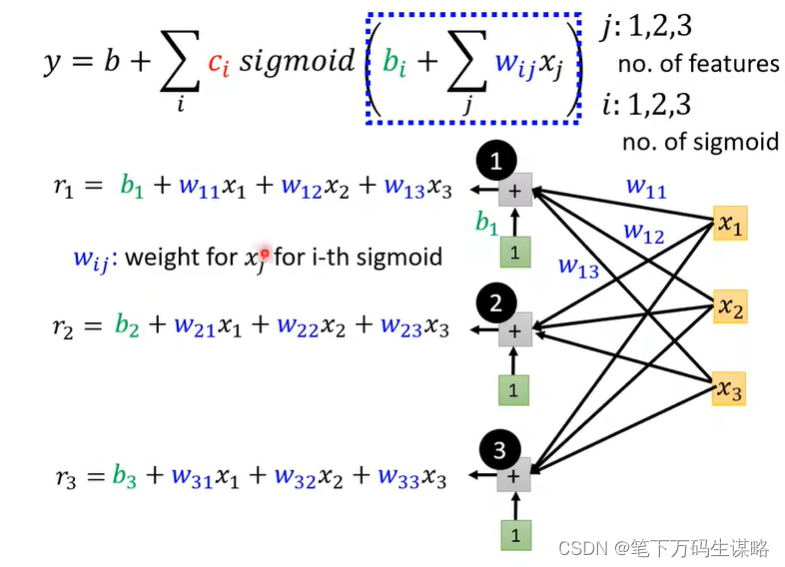
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1,x2,x3与
r
1
,
r
2
,
r
3
r_1,r_2,r_3
r1,r2,r3的关系我们可以用矩阵表示出来:

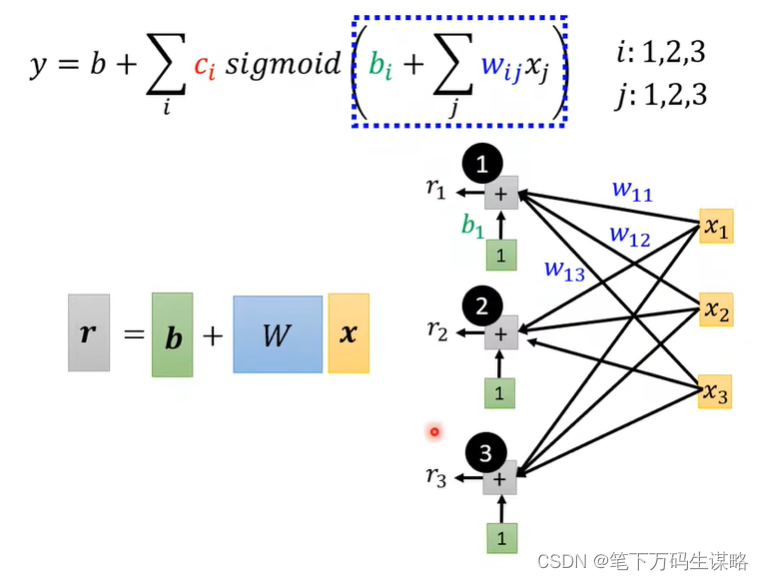
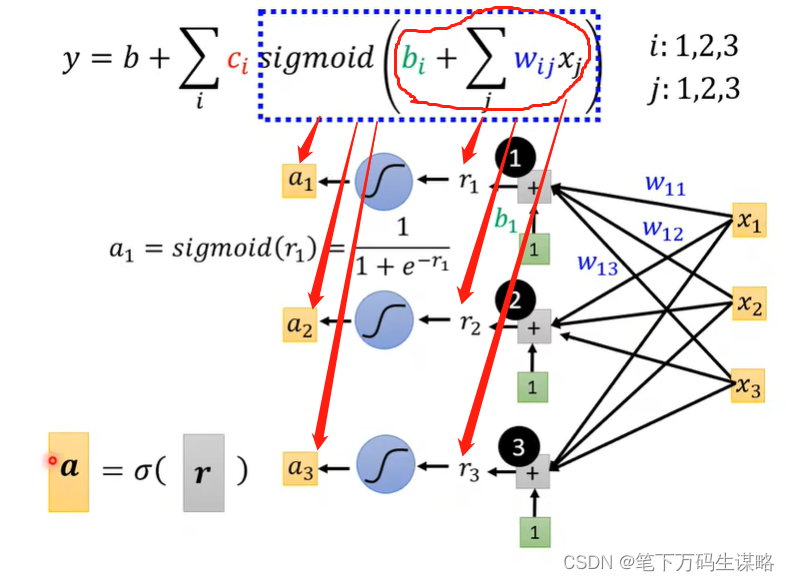
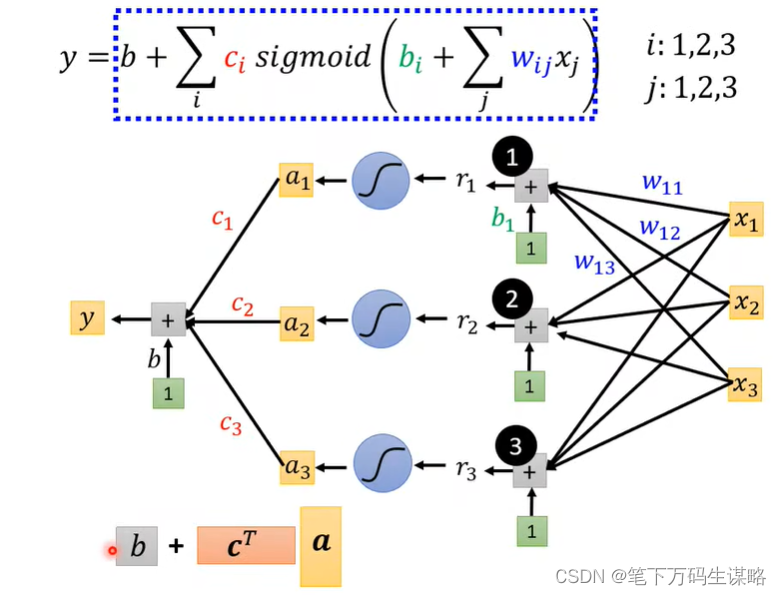
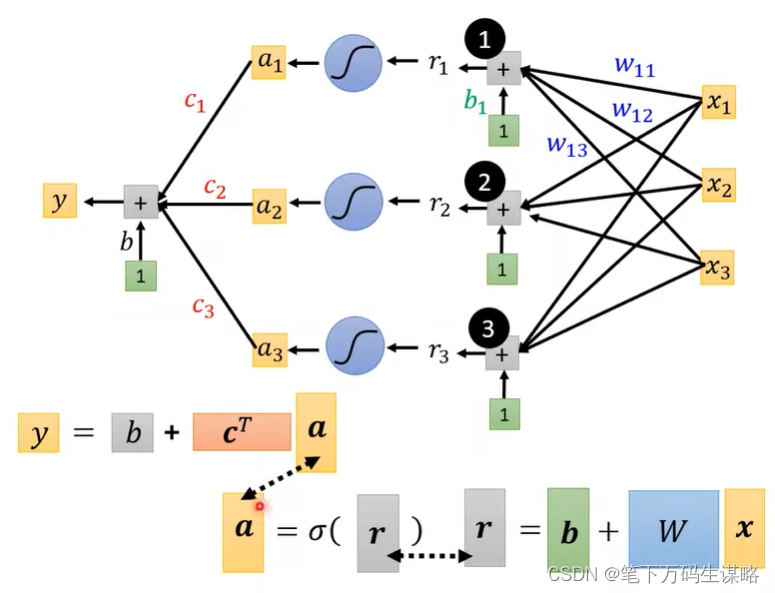
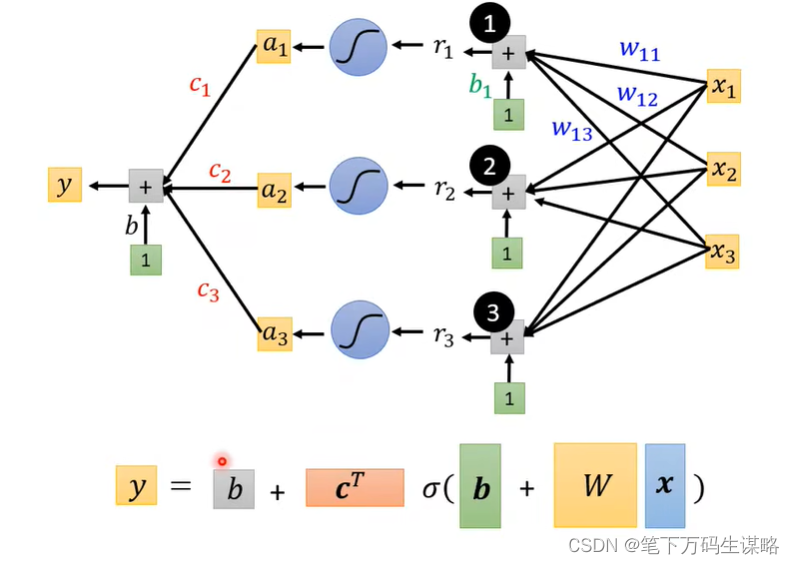
Back to framework
1.带有未知数的函数:

特征与参数:
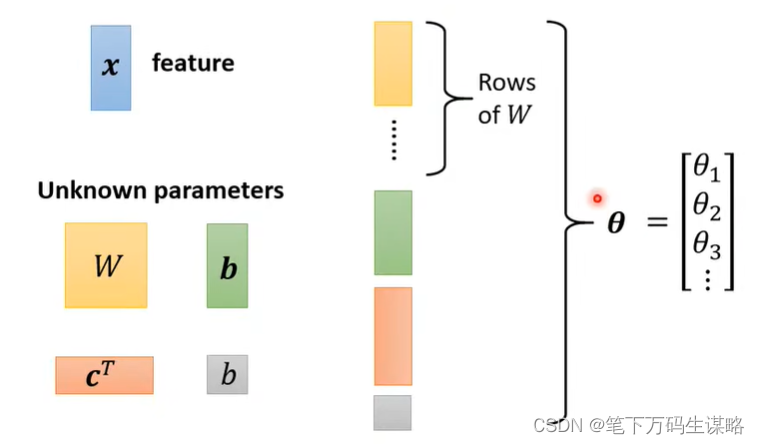
2.定义损失(从训练数据进行计算)
Loss是参数的函数
L
(
θ
)
L(\theta)
L(θ)
Loss意味着一套参数值有多好
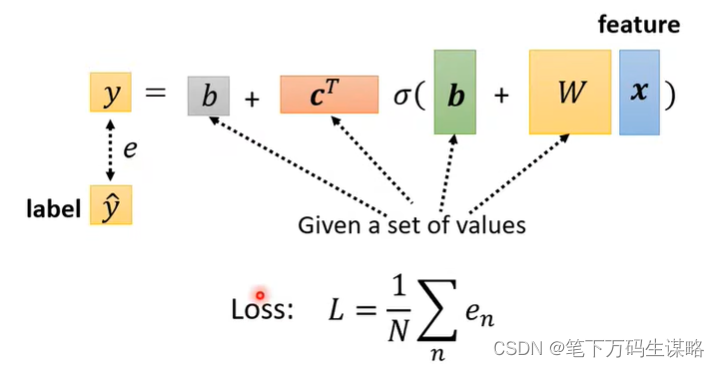
3. 最优化

- 随机选取初始点 θ 0 \theta_0 θ0
- 计算微分
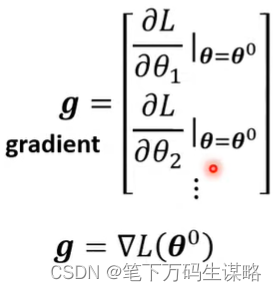
(就是看左右哪边高,向低的跨步)
若求出为负值(左高右低的切线),增大w,loss就变小;若求出为正值(左低右高的切线),减小w,loss就变大。
- 更新迭代w
步子跨多大,取决于:1.斜率(斜率大就跨大一点),2学习率(自己设定的)
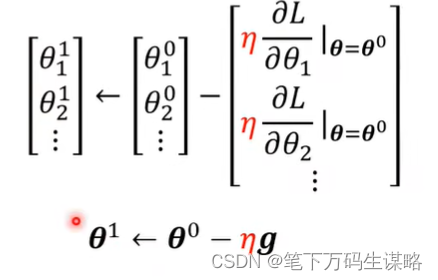

直到你不想做了,或计算出的gradient为零向量。
实际做gradient decent:
N的数据分成多个Batch,计算loss,更新参数。
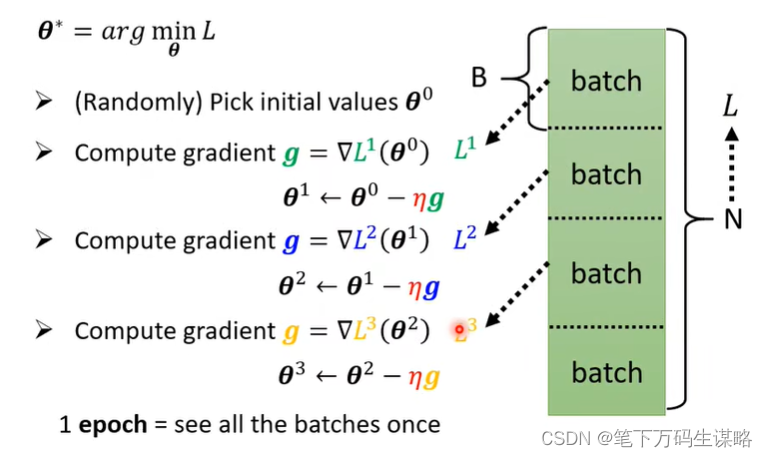
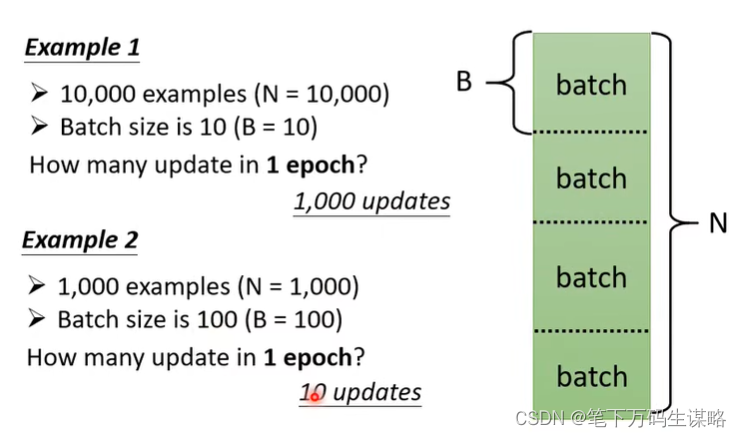
为什么Hard Sigmoid 要换成Soft Sigmoid?
Hard Sigmoid 表示:
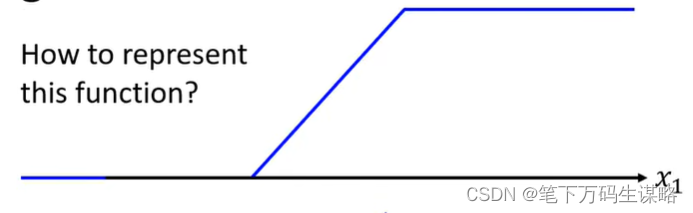
ReLU函数:
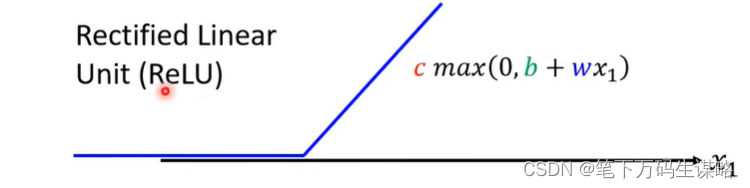
从ReLU到Sigmoid:(2个ReLU合成Sigmoid)
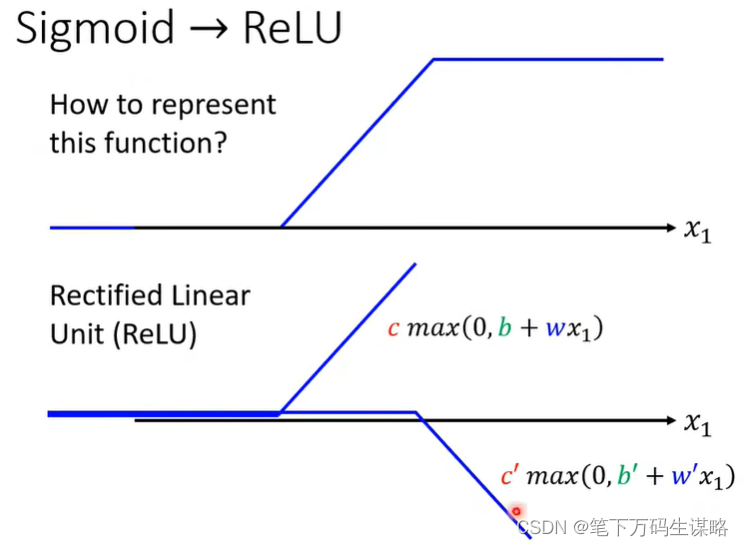
4.激活函数
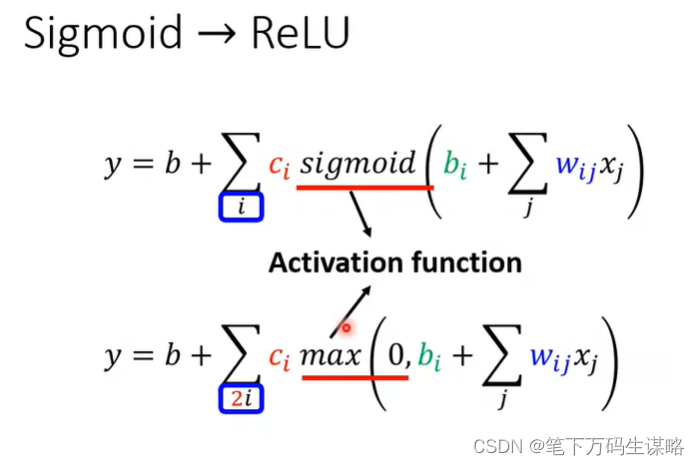

5.继续改我们的模型

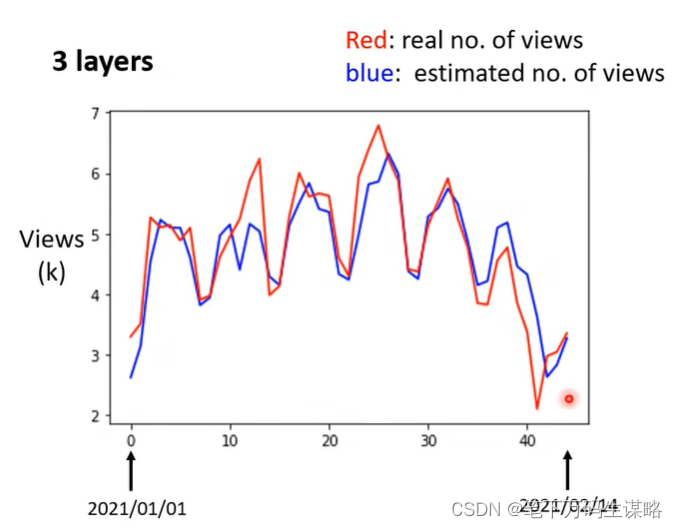
机器02/14左右高估了,因为除夕。
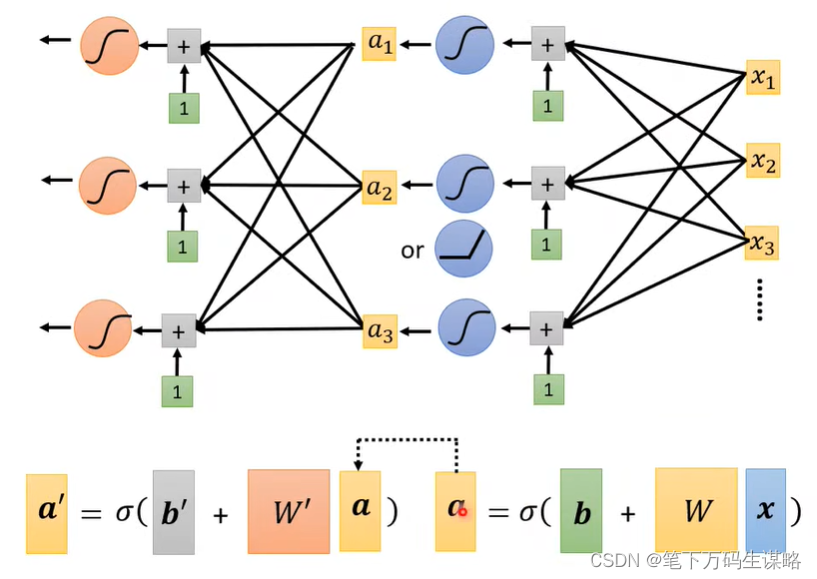
三、Neural Network
那这个 Sigmoid 或是 ReLU,它们在机器学习里面叫做 Activation Function 激活函数。 这些Sigmoid 或 ReLU ,它们叫做 Neuron 神经元。我们这边有很多的 Neuron,很多的 Neuron 就叫做 Neural Network。
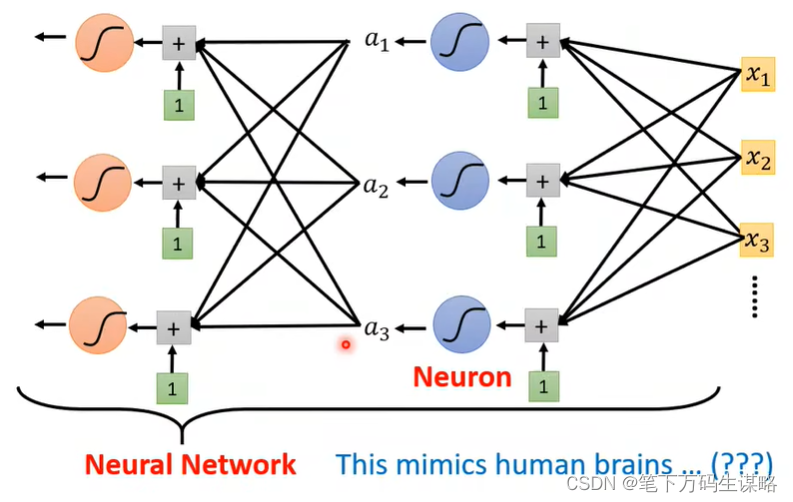
每一排neourn叫做hidden layer,许多layer就叫做Deep Learning。
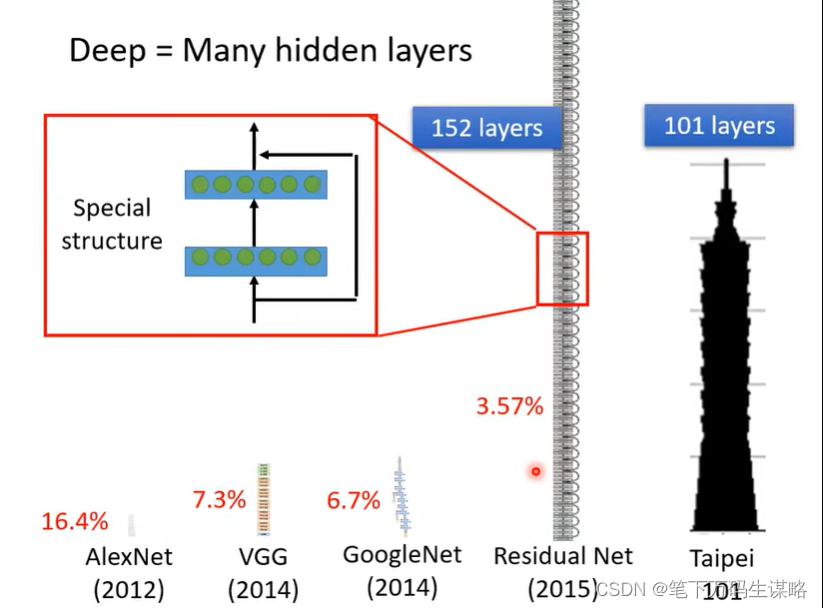
为什么不做的更深呢?
会过拟合,即在训练资料上变好,在没训练的资料上变差
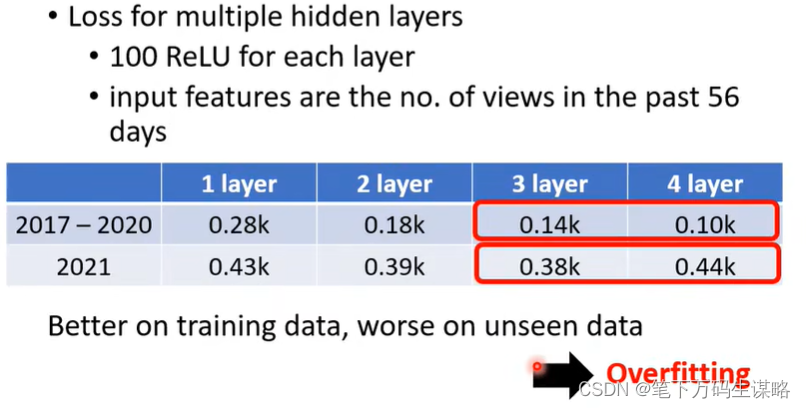
预测未知资料