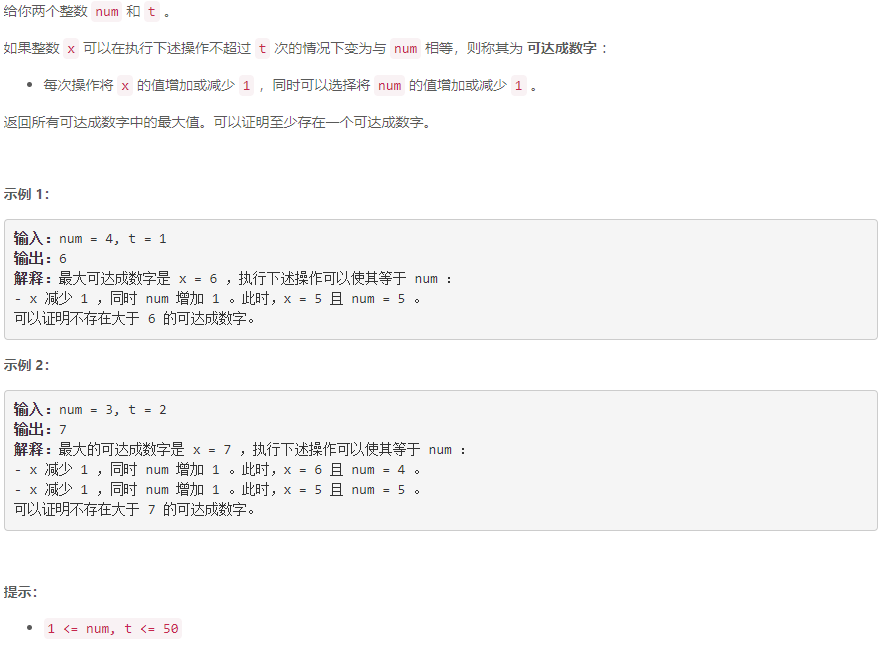
A 找出最大的可达成数字
签到题
class Solution {
public:
int theMaximumAchievableX(int num, int t) {
return num+t*2;
}
};
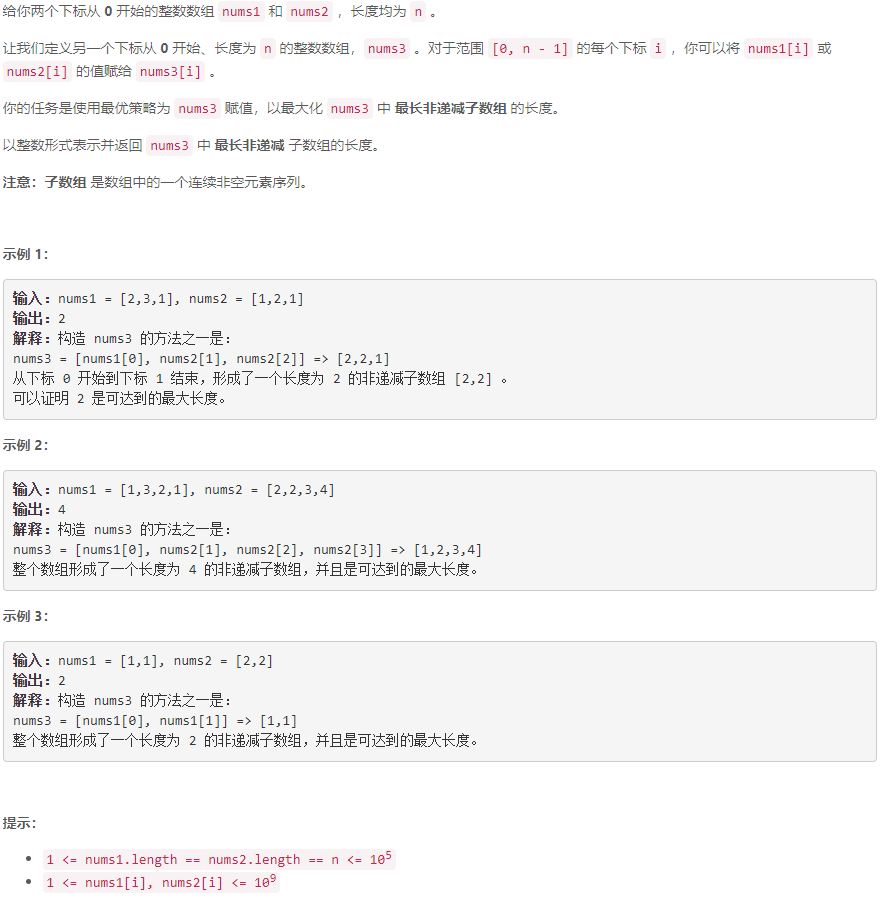
B 达到末尾下标所需的最大跳跃次数

动态规划: 定义 p i p_i pi为跳至 i i i处所需的最大跳跃次数, 有状态转移方程 p i = m a x { p j + 1 ∣ 0 ≤ j < i , a b s ( n u m s [ i ] − n u m s [ j ] ) ≤ t a r g e t } p_i=max\{ p_j+1 \;|\; 0\le j< i, abs(nums[i]-nums[j])\le target \} pi=max{pj+1∣0≤j<i,abs(nums[i]−nums[j])≤target}
class Solution {
public:
int maximumJumps(vector<int> &nums, int target) {
int n = nums.size();
vector<int> p(n, INT32_MIN);
p[0] = 0;
for (int i = 1; i < n; i++)
for (int j = 0; j < i; j++)
if (p[j] != INT32_MIN && abs(nums[i] - nums[j]) <= target)
p[i] = max(p[i], p[j] + 1);
return p[n - 1] == INT32_MIN ? -1 : p[n - 1];
}
};
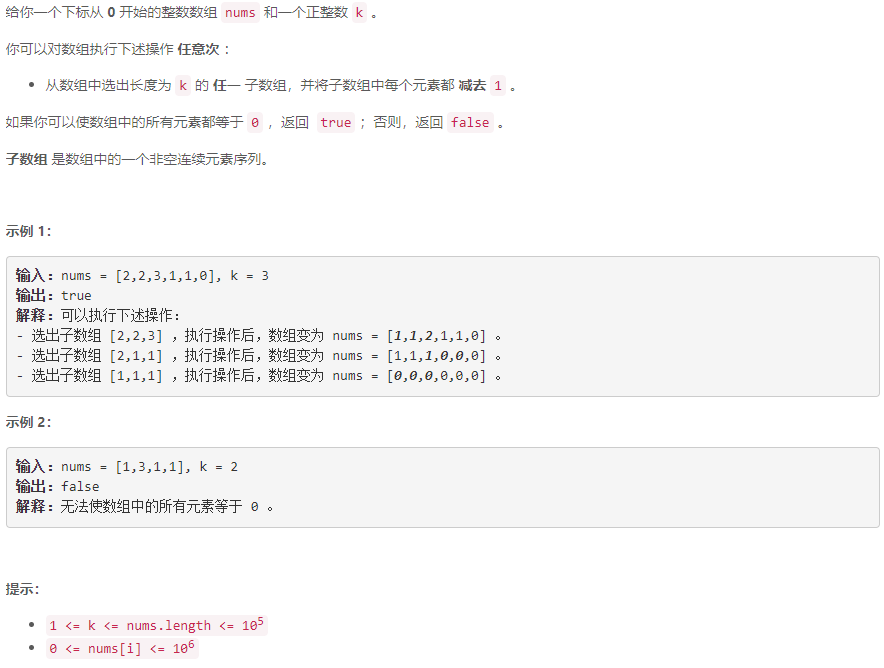
C 构造最长非递减子数组
动态规划: 定义
p
i
,
0
p_{i,0}
pi,0为下标
i
i
i选
n
u
m
s
1
[
i
]
nums1[i]
nums1[i]情况下
n
u
m
s
3
[
0
,
i
]
nums3[0,i]
nums3[0,i]中以
n
u
m
s
3
[
i
]
nums3[i]
nums3[i]结尾的最长非递减子数组的长度, 类似地定义
定义
p
i
,
1
p_{i,1}
pi,1为下标
i
i
i选
n
u
m
s
2
[
i
]
nums2[i]
nums2[i]情况下
n
u
m
s
3
[
0
,
i
]
nums3[0,i]
nums3[0,i]中以
n
u
m
s
3
[
i
]
nums3[i]
nums3[i]结尾的最长非递减子数组的长度,
p
i
,
j
p_{i,j}
pi,j只有两种可能的前驱状态
p
i
−
1
,
0
p_{i-1,0}
pi−1,0、
p
i
−
1
,
1
p_{i-1,1}
pi−1,1.
class Solution {
public:
int maxNonDecreasingLength(vector<int> &nums1, vector<int> &nums2) {
int n = nums1.size();
int p[n][2];
p[0][0] = 1;
p[0][1] = 1;
int res = 1;
for (int i = 1; i < n; i++) {
p[i][0] = max(nums1[i] >= nums1[i - 1] ? p[i - 1][0] + 1 : 1, nums1[i] >= nums2[i - 1] ? p[i - 1][1] + 1 : 1);
p[i][1] = max(nums2[i] >= nums1[i - 1] ? p[i - 1][0] + 1 : 1, nums2[i] >= nums2[i - 1] ? p[i - 1][1] + 1 : 1);
res = max(res, p[i][0]);
res = max(res, p[i][1]);
}
return res;
}
};
D 使数组中的所有元素都等于零
差分数组: 遍历数组同时用差分数组维护当前位置已经减掉的值 c u r cur cur, 若遍历到下标为 i i i时: 1) n u m s [ i ] − c u r > 0 nums[i]-cur>0 nums[i]−cur>0 代表需要在 [ i , i + k − 1 ] [i,i+k-1] [i,i+k−1]这段区间减 c u r − n u m s [ i ] cur-nums[i] cur−nums[i](若 i + k − 1 i+k-1 i+k−1越界返回false),2) n u m s [ i ] − c u r < 0 nums[i]-cur<0 nums[i]−cur<0 返回 f a l s e false false. 遍历结束返回 t r u e true true.
class Solution {
public:
bool checkArray(vector<int> &nums, int k) {
int n = nums.size();
vector<int> d(n + 2);
for (int i = 0, cur = 0; i < n; i++) {
cur += d[i];//差分数组上的前缀和
if (nums[i] - cur > 0) {
if (i + k - 1 >= n)
return false;
d[i + k] -= nums[i] - cur;//更新差分数组d[i+k]
cur += nums[i] - cur;
} else if (nums[i] - cur < 0)
return false;
}
return true;
}
};