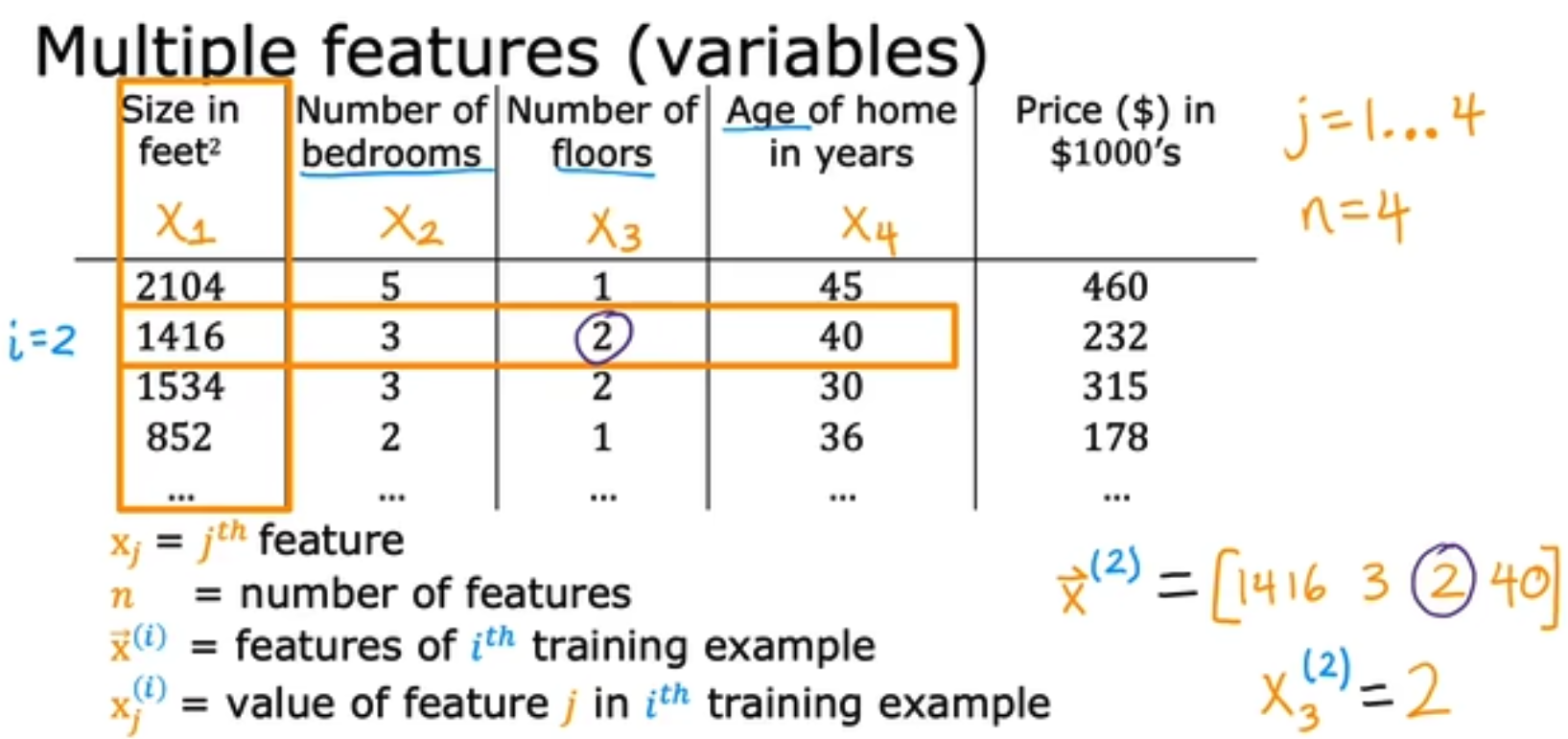
在进行多元线性回归的时候,我们需要规定一些基本法则。例如我们使用 x j ( i ) x_j^{(i)} xj(i)来表示第i个sample的第j个特征。
将单元的线性回归变为多元线性回归,公式将变换为如下,
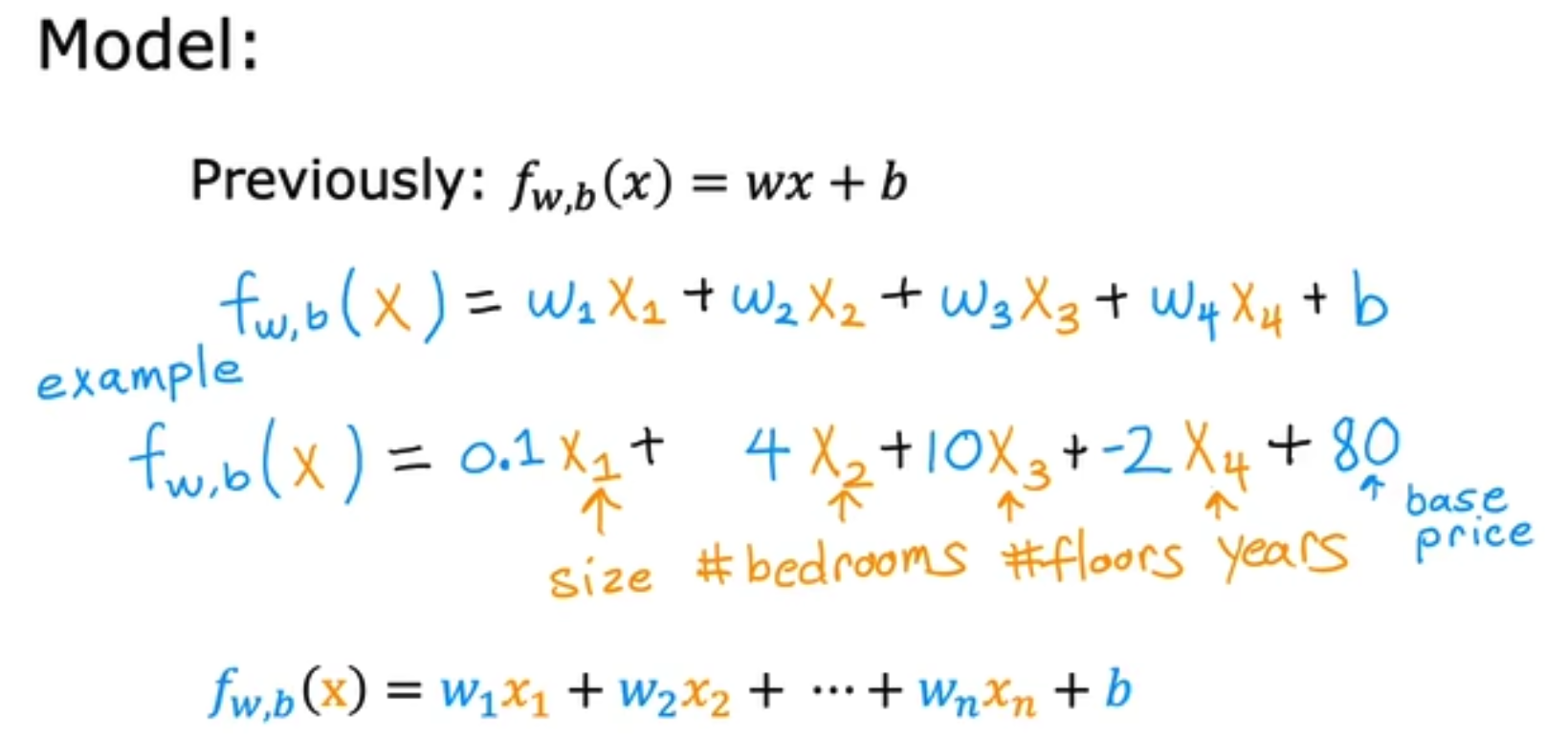
为了实现更简单的数学表达式,我们将表达式向量化,得到了multiple linear regression, not multivariate regression(是多元线性回归,不是多元回归),注意由于对应多个特征,所有只有w和x是多维的,而b只是一个一维标量。
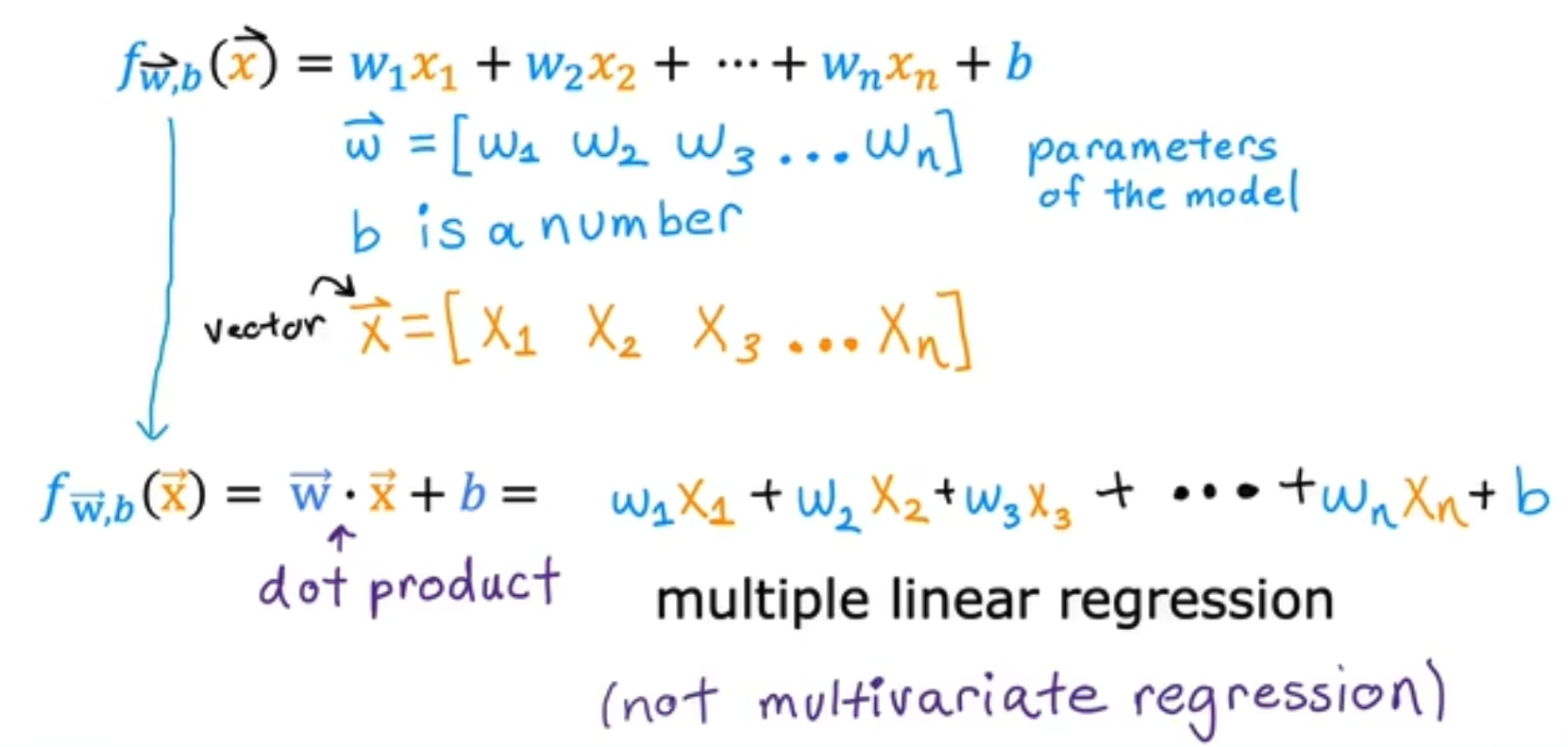
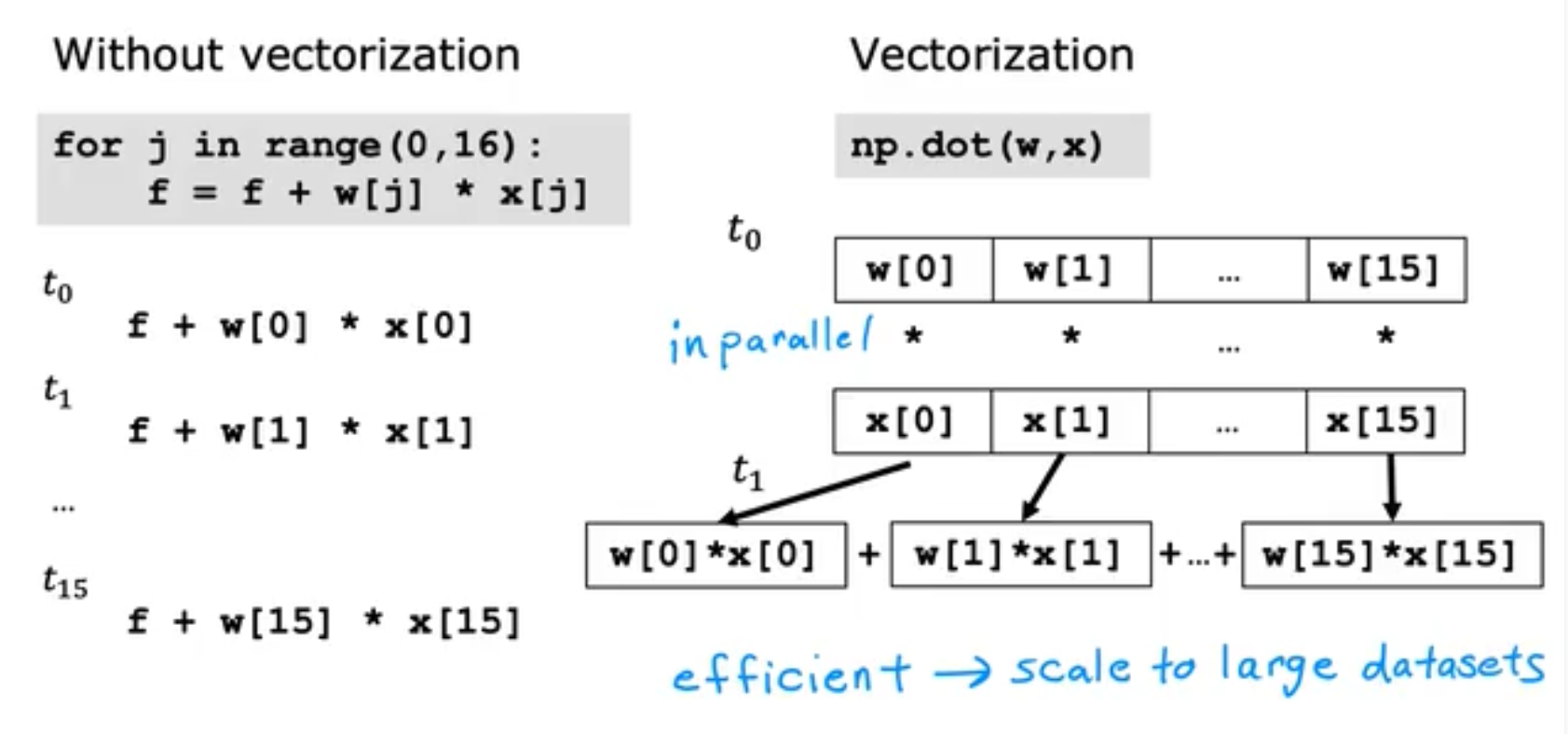
接下来我们再来更加深入地讲解一下vectorization向量化/矢量化。在线性代数中我们知道,矩阵的引入简化了方程组的计算,在计算机和深度学习中亦是如此,当我们使用矩阵进行运算时,不仅可以简洁代码,甚至由于Pytorch/Tensorflow等底层代码还能为GPU加速,Numpy为CPU加速。接下来我们来比较两种不使用vectorization和一种使用vectorization的区别,所以我们建议将所有的参数(weight权重,bias偏置)和输入(feature特征)都采用矩阵或者向量来表示,

接下来我们将更加深入地了解Vectorization的作用,那么为什么Vctorization能带来速度的提升呢?很大一部分原因是因为他在计算机内部的运行往往是并行的,以for循环为例,for循环是一步一步串行计算的;而dot则是先全部in parallel并行计算完毕,再一次性将结果相加,过程比较如下:

在了解了向量化能够带来的优势后,我们用向量化来表达多元线性回归,我们将w和x向量化,得到如下的表示,

我们重点来了解一下偏微分的部分,假设我们有n个feature,m个sample,我们对单个feature求偏微分就应该对m个sample都求偏微分再求平均,如下,
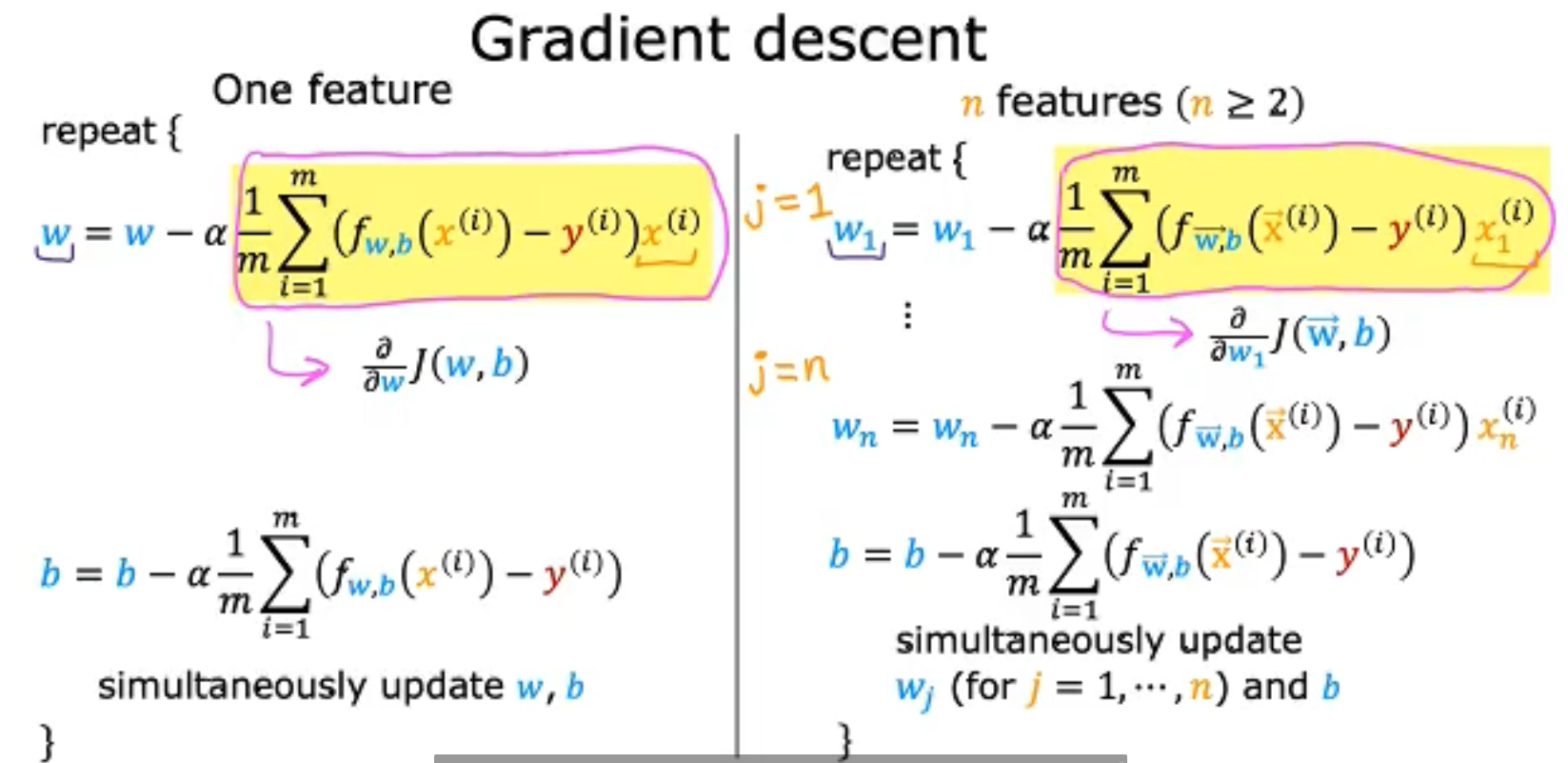
同时,除了使用Gradient Descent来求解Linear Regression的解之外,我们还可以使用Normal equation法方程来求解,但是它并不像是GD能推广到别的机器学习如卷积神经网络上。我们需要注意到的是在一些机器学习库的后端,很有可能会使用Normal equation来求解Linear Regression的参数,因为这个方法更快。