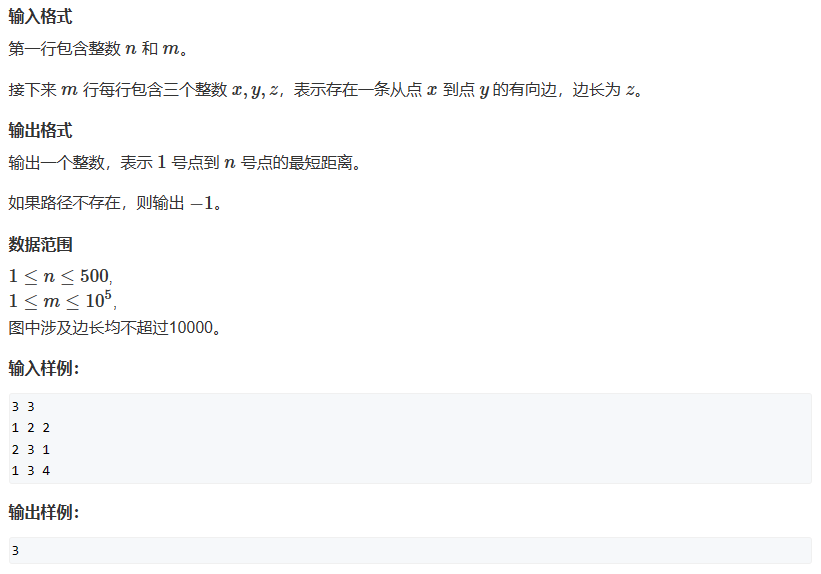
给定一个 n个点 m 条边的有向图，图中可能存在重边和自环，所有边权均为正值。请你求出 1号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

#include<iostream>
#include<fstream>
#include<cstring>
#include<stdio.h>

using namespace std;

const int N = 1e3+10;
int g[N][N];//邻接矩阵
int dis[N];//起点到某个点的距离
int st[N];//已确定的点
int n,m;//n个点 m条边


int dijkstra(int u){
        memset(dis,0x3f,sizeof dis);//初始距离为无穷
        dis[u] = 0;

        for(int i = 1;i <= n;i++){//遍历所有的顶点
            /**
             *Extract-Min操作
             */            
            int t = -1;//选择下一个顶点
            for(int j = 1;j <= n;j++){//找出当前点最短的出边的下一个顶点
                if(!st[j] && (t == -1 || dis[j] < dis[t])){//j顶点不在S集合 并且t未确定或者t确定但找到j距离小于t
                    t = j;
                }
            }
            st[t] = 1;//循环结束后 t也就确定了  将t加入S集合
            
            /**
             * Relax操作
             * 因为S集合增加了新的点
             * 所以更新每个点的最短距离
             */
             for(int i = 1;i<=n;i++){//找一个点，如果先到t再到i的距离比原来直接到i更短，就替换该距离
                 dis[i] = min(dis[i], dis[t] + g[t][i]);
             }
             
        }

     
    if(dis[n] > 10000){//说明1无法到达n
        return -1;
    }
    
    return dis[n];
}

int main(){
    memset(g,0x3f,sizeof g);//初始化所有边长均为正无穷
    cin>>n>>m;
    //因为可能存在重边，所以u到v的重边只要保留最短边即可
    int x,y,z;
    for(int i = 1;i<=m;i++){
        cin>>x>>y>>z;
        g[x][y] = min(g[x][y],z);
    }
    
    cout<<dijkstra(1);
    return 0;
}

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;

typedef pair<int,int> pii;

const int N = 1e5+10;
//稀疏图用邻接表，并且这么大的N如果直接开数组，二维数组会报错
int h[N], e[2*N], ne[2*N], w[2*N];//多一个权值
int idx;

int dis[N];//起点到某点的距离
priority_queue<pii,vector<pii>,greater<pii>> heap;//小顶堆  队头是距离最小的元素
int st[N];//如果有重边，在添加过程中就会出现重复的边在堆内，但由于会优先取最小距离的边，所以冗余边没关系
int n,m;

void add(int a,int b, int c){//添加a到b的边 权值为c
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++; 
}

int dijkstra(int u){
    memset(dis,0x3f,sizeof dis);
    dis[u] = 0;
    heap.push({0,1});
    
    while(!heap.empty()){
        auto t = heap.top();
        heap.pop();
        int ver = t.second, distance = t.first;//距离
        if(st[ver]) continue;//冗余边，已经访问过，可以跳过，因为每次优先取更小的边，访问到已访问过的说明这次的距离更大
        st[ver] = 1;//标记访问过的边
        
        /**
        *把Extract-Min操作和Relax操作一起完成了
        */
        for(int i = h[ver];i != -1;i = ne[i]){
            int j = e[i];//取编号
            /**
             *distance为起点到ver的距离 ， w[i]为ver到e[i]的的距离 
             *如果 起点直接到j距离 比 起点到ver再到e[i] 更远，那么就更新dis[j]
             */
            dis[j] = min(dis[j],distance + w[i]);
            heap.push({dis[j],j});//可以直接添加，冗余的会跳过
        }
        
    }
    if(dis[n] == 0x3f3f3f3f) return -1;
    return dis[n];
}


int main(){
    memset(h,-1,sizeof h);
    cin>>n>>m;
    int x,y,z;
    
    while(m--){
        cin>>x>>y>>z;
        add(x,y,z);
    }
    
    cout<<dijkstra(1);
    return 0;
}