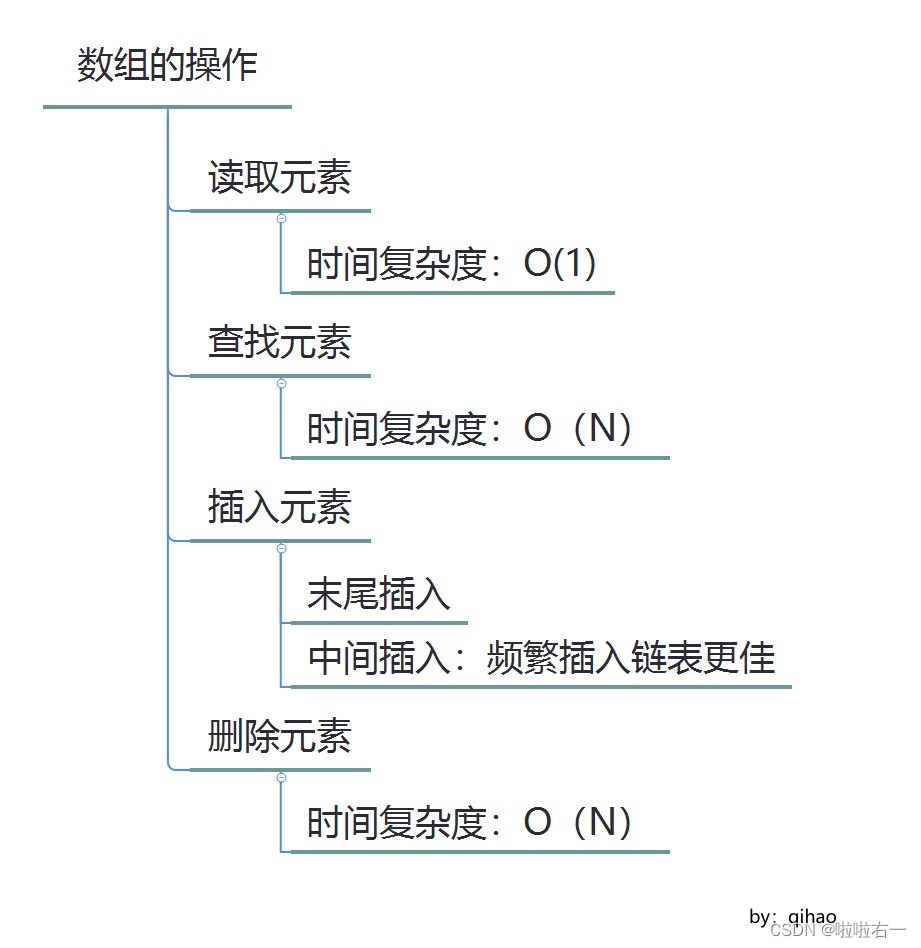
数组是数据结构中的基本模块之一。因为字符串是由字符数组形成的,所以二者是相似的。力扣LeetBook——数组和字符串
文章目录
- 📚数组简介
- 👉寻找数组的中心索引
- 👉搜索插入位置
- 👉合并区间
- 📚二维数组简介
- 👉旋转矩阵
- 👉零矩阵
- 👉对角线遍历
- 📚字符串简介
- 👉最长公共前缀
- 👉最长回文子串
- 👉翻转字典串里的单词
- 👉实现strStr()
📚数组简介
以下思维套图来源于讨论区——七号7毫升⭐️
👉寻找数组的中心索引
-
直接暴力思路,超时了😢
class Solution { public: int pivotIndex(vector<int> &nums) { int sum1,sum2; for(int i=0;i<nums.size();i++) { //中心下标为0的情况 if(i==0) { sum1 = 0; for(int j=1;j<nums.size();j++) { sum2 += nums[j]; } if(sum1 == sum2) { return 0; } sum2 = 0; } //其他 else { //左边的和 for(int k=0;k<i;k++) { sum1 += nums[k]; } //右边的和 for(int j=i+1;j<nums.size();j++) { sum2 += nums[j]; } if(sum1==sum2) { return i; } //归零 sum1=0; sum2=0; } } return -1; } };
-
改良,考虑
左边×2+sum[i]=总和class Solution { public: int pivotIndex(vector<int> &nums) { int sum=0; for(int i=0;i<nums.size();i++) {//先求和 sum += nums[i]; } int sum1=0; for(int i=0;i<nums.size();i++) { if(2*sum1+nums[i]==sum) { return i; } sum1 += nums[i]; } return -1; } };
👉搜索插入位置
-
直接暴力循环查找
class Solution { public: int searchInsert(vector<int>& nums, int target) { for(int i=0;i<nums.size();i++) { if(nums[i]>=target) { return i; } } return nums.size(); } };
-
改良,因为是升序数组,所以用二分
class Solution { public: int searchInsert(vector<int>& nums, int target) { int left=0,right=nums.size()-1; while(left<=right) { int mid=left+(right-left)/2; if(nums[mid]<target) left=mid+1; else right=mid-1; } return left; } };
👉合并区间
参考官方题解和一位匿名用户的题解——排序

class Solution {
public:
//函数名称是 merge,它有一个参数 intervals
//这个参数是一个引用类型的二维向量 vector<vector<int>>。
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if(intervals.size() == 1)
{//此时不需要合并
return intervals;
}
//先排序,根据Start先排序,确保前一个的Start小于后一个
sort(intervals.begin(),intervals.end());
vector<vector<int>> res;
res.push_back(intervals[0]);//先把第一个压入
int j = 0;//基数组,以此作为基础合并
for(int i = j + 1;i < intervals.size();i++)
{
//判断,如果第二个子数组的start小于前一个的End,就合并,否则直接压入
if(intervals[i][0] <= res[j][1])
{
//判断前后两个子数组End值大小,取最大的为End
//因为之前排序过,所以Start是前一个较小,这里不需要再做判断
res[j][1] = max(res[j][1],intervals[i][1]);
}
else
{
res.push_back(intervals[i]);
j++;
}
}
return res;
}
};

⭐️sort函数详解
📚二维数组简介
👉旋转矩阵
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int n=matrix.size();
for(int i=0;i<n-1; i++)
{//先是行列转换
for(int j=i+1;j<n;j++)
{
swap(matrix[i][j], matrix[j][i]);
}
}
for(int i=0; i!=n;i++)
{//然后镜像翻转
for(int j=0; j<n/2;j++)
{
swap(matrix[i][j], matrix[i][n-j-1]);
}
}
}
};

👉零矩阵
class Solution {
public:
void setZeroes(vector<vector<int>>& matrix) {
int rsize = matrix.size(); //行数
int csize = matrix[0].size();//列数
vector<vector<int>> m;//记录值为0的元素的位置
for(int i=0;i<rsize;i++)
{//找到0元素所在位置,标记
for(int j=0;j<csize;j++)
{
if(matrix[i][j]==0)
{
m.push_back({i,j});
}
}
}
for(int i=0; i<m.size(); i++)
{//替换
int j=m[i][0]; //行
int k=m[i][1]; //列
for(int i=0;i<csize;i++)
{
matrix[j][i]=0;
}
for(int i=0;i<rsize;i++)
{
matrix[i][k]=0;
}
}
}
};

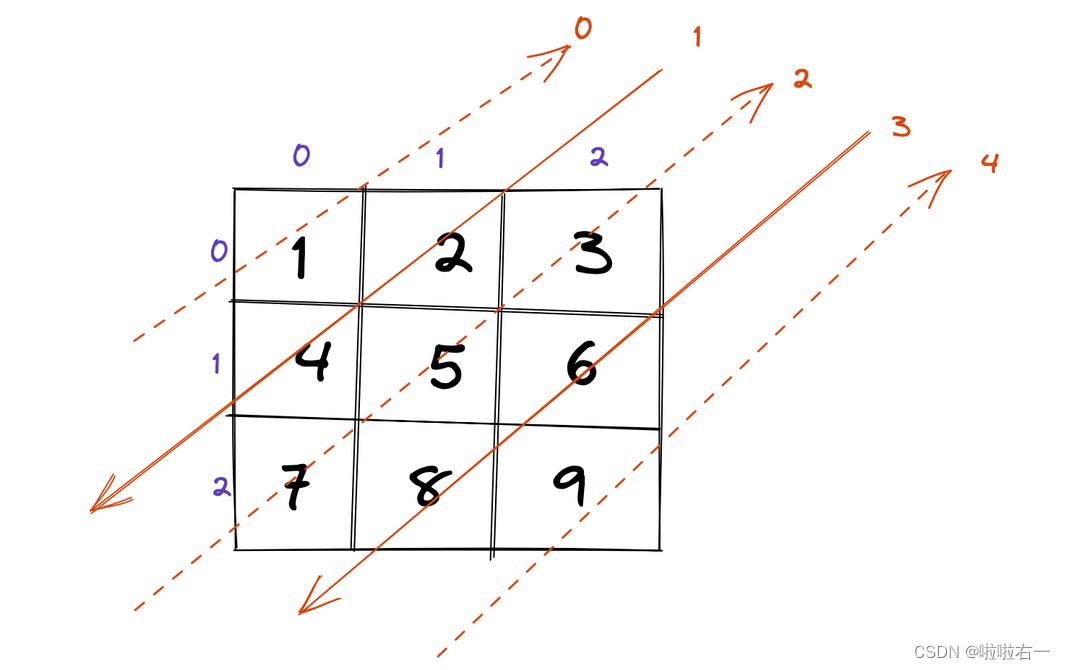
👉对角线遍历
参考官方题解:直接模拟对角线走向
class Solution {
public:
vector<int> findDiagonalOrder(vector<vector<int>>& mat) {
int m=mat.size();//获取矩阵的行数
int n=mat[0].size();//获取矩阵的列数
vector<int> res;//创建一个空向量,用于存储结果
for (int i=0;i<m+n-1; i++)
{//遍历所有可能的对角线索引
if(i%2)
{//奇数索引的对角线
int x=i<n?0:i-n+1;//计算第一个元素的行索引
int y=i<n?i:n-1;//计算第一个元素的列索引
while(x<m && y>=0)
{//遍历当前对角线上的所有元素
res.emplace_back(mat[x][y]);//将当前元素添加到结果向量中
x++;//行索引递增
y--;//列索引递减
}
}
else
{//偶数索引的对角线
int x=i<m?i:m-1;
int y=i<m?0:i-m+1;
while(x>=0 && y<n)
{
res.emplace_back(mat[x][y]);//将当前元素添加到结果向量中
x--;//行索引递减
y++;//列索引递增
}
}
}
return res;
}
};
push_back和emplace_back都是 STL 中 vector 的函数,用于在 vector 的尾部添加元素。但是它们的区别在于添加元素的方式不同。
push_back接受已经构造好的对象作为参数,然后将其加入到 vector 的尾部。
emplace_back接受参数,直接在 vector 的尾部构造对象。因此
emplace_back更高效,因为它避免了构造对象的临时副本。
📚字符串简介
👉最长公共前缀
class Solution {
public:
string longestCommonPrefix(vector<string>& strs)
{
string all;
all = strs[0]; // all字符串保存第一个字符串
for (int i = 1; i < strs.size(); i++)
for (int j = 0; j < all.size(); j++)
if (all[j] != strs[i][j]) // 比较all字符串和当前字符串的每个字符
all.erase(j); // 如果不相等,则删除j及其后面的字符
return all; // 返回最长公共前缀字符串
}
};

⭐️erase函数应用
👉最长回文子串
参考官方题解+动态规划
class Solution {
public:
string longestPalindrome(string s) {
int n=s.size();
if(n<2)
return s;
//定义状态数组,dp[i][j]表示从s字符串中第i个字符到第j个字符的子串是否为回文串。
//vector<vector<bool>> dp: 这是一个二维向量,每个元素都是一个布尔值。
//(n, vector<bool>(n, false)): 这部分表示用 n 作为行数和列数来初始化二维矩阵。每个元素都被初始化为 false。
vector<vector<bool>> dp(n, vector<bool>(n, false));
//初始化单个字符的情况
for(int i=0;i<n; i++)
dp[i][i]=true;
int maxLen=1;//记录最长回文子串的长度
int start=0;//记录最长回文子串的起始位置
//枚举子串长度
for(int len=2;len<=n;len++)
{
//枚举子串起始位置
for(int i=0;i<n-len+1; i++)
{
int j=i+len-1;
//当子串两端字符相等时
if(s[i]==s[j])
{
//如果子串长度小于等于2,则必定为回文子串
//如果子串长度大于2,则根据dp[i+1][j-1]的结果判断是否为回文子串
if (len<=2 || dp[i+1][j-1])
{
dp[i][j]=true;
if (len>maxLen)
{//更新
maxLen=len;
start=i;
}
}
}
}
}
//返回从start位置开始的maxLen个字符,提取出最长回文子串。
return s.substr(start, maxLen);
}
};
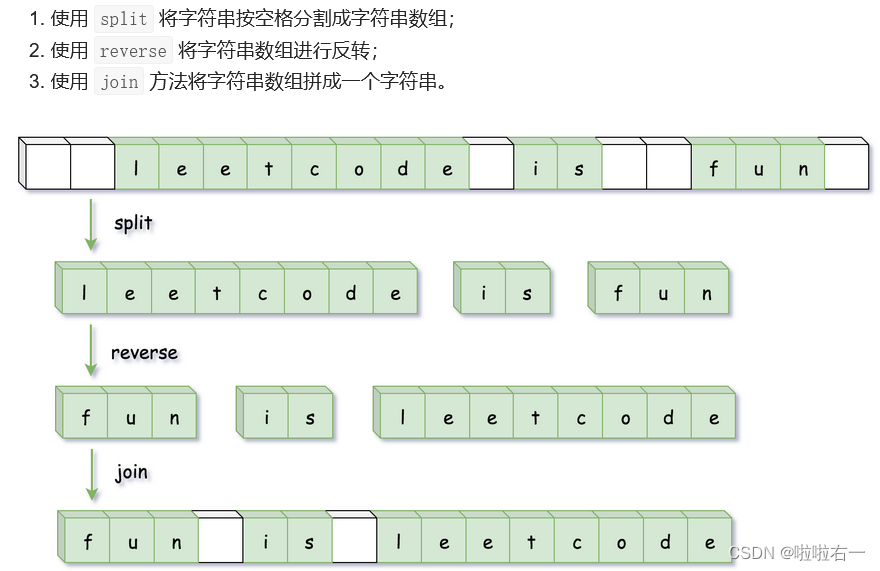
👉翻转字典串里的单词
-
首先,定义了两个辅助字符串变量:word用于存储当前正在构建的单词,result用于存储最终结果。
-
然后,开始遍历 s字符串。
- 对于每个字符,如果该字符不是空格,则将其加入到当前正在构建的单词 word中。
- 当遇到一个空格时,如果前一个字符不是空格,说明一个单词已经构建完成。
- 此时,将当前构建好的单词添加到结果字符串 result中,并在两个单词之间添加一个空格。
- 然后清空当前单词 word,准备构建下一个单词。
-
接下来,处理最后一个单词。如果最后一个单词非空,则将其添加到结果字符串 result中。如果 result为空,则直接将最后一个单词作为结果字符串。
-
最后,返回结果字符串 result。
class Solution {
public:
string reverseWords(string s) {
int n=s.size();
string word=""; //存储当前正在构建的单词
string result=""; //存储最终结果
for(int i=0;i<n;i++)
{
if(s[i]!=' ')
{//如果当前字符不是空格,则将其加入到当前正在构建的单词中
word += s[i];
}
else if(i>0 && s[i-1]!=' ')
{//如果当前字符是空格,并且前一个字符不是空格,则说明一个单词已经构建完成
//将当前构建好的单词添加到结果字符串result中,并在两个单词之间添加一个空格
result=(result.empty()?word:word+" "+result);
word="";//清空当前单词,准备构建下一个单词
}
}
//处理最后一个单词
if (!word.empty())
{
//如果最后一个单词非空,则将其添加到结果字符串result中
//如果result为空,则直接将最后一个单词作为结果字符串
result=(result.empty()?word:word+" "+result);
}
return result;
}
};

python——使用语言特性
class Solution:
def reverseWords(self, s: str) -> str:
return " ".join(reversed(s.split()))
👉实现strStr()
class Solution {
public:
int strStr(string haystack,string needle) {
if(needle.empty())
{//如果needle为空字符串,则返回0
return 0;
}
int pos=haystack.find(needle);//在haystack中搜索needle
//string::npos是一个常量,表示未找到。
if(pos!=string::npos)
{//如果找到了
return pos;
}
return -1; //没有找到,返回-1
}
};