数据结构 | 二叉排序树

news2024/11/26 20:26:41

一、数据结构定义

/* 二叉排序树 */
typedef int TreeType;
typedef struct BSTNode {
	TreeType data;
	struct BSTNode* lchild, * rchild;
}*BSTree, BSTNode;

二、方法概览

BSTNode* CreateTreeNode(TreeType data); // 创建二叉树结点
BSTNode* InsertTree(TreeType data, BSTree root); // 插入元素
void PreOrder(BSTree T); // 先序遍历
void InOrder(BSTree T);	 // 中序遍历
BSTree FindMin(BSTree T);  // 查找最小值，返回该结点
BSTree FindMax(BSTree T);  // 查找最大值，返回该结点
BSTree FindKey_nonrecursion(BSTree T, TreeType key);	// 查找指定数据元素(非递归)
BSTree FindKey_recursion(BSTree T, TreeType key);		// 查找指定数据元素(递归)
BSTree DeleteData(BSTree T, TreeType element);			// 删除指定元素的结点

三、方法详解

// 创建二叉树结点
BSTNode* CreateTreeNode(TreeType data) {
	BSTNode* p = (BSTNode*)malloc(sizeof(struct BSTNode));
	p->lchild = p->rchild = NULL;
	p->data = data;
	return p;
}
// 插入元素
BSTNode* InsertTree(TreeType data, BSTree root){
	if (root == NULL) {
		root = CreateTreeNode(data);
		return root;
	}
	if (data < root->data)
		root->lchild = InsertTree(data, root->lchild);
	if (data > root->data)
		root->rchild = InsertTree(data, root->rchild);
	return root;
}
// 先序遍历
void PreOrder(BSTree T){
	if (T == NULL) return;
	printf("%d ", T->data);
	PreOrder(T->lchild);
	PreOrder(T->rchild);
}
// 中序遍历
void InOrder(BSTree T){
	if (T == NULL) return;
	InOrder(T->lchild);
	printf("%d ", T->data);
	InOrder(T->rchild);
}
// 查找最小值，返回该结点
BSTree FindMin(BSTree T){
	if (T == NULL) return NULL;
	BSTree min = T;
	while (min->lchild != NULL)
		min = min->lchild;
	return min;
}
// 查找最大值，返回该结点
BSTree FindMax(BSTree T){
	if (T == NULL) return NULL;
	BSTree max = T;
	while (max->rchild != NULL)
		max = max->rchild;
	return max;
}
// 查找指定数据元素(非递归)
BSTree FindKey_nonrecursion(BSTree T, TreeType key) {
	while (T != NULL && key != T->data) {
		if (T->data > key) T = T->lchild;
		else T = T->rchild;
	}
	return T;
}
// 查找指定数据元素(递归)
BSTree FindKey_recursion(BSTree T, TreeType key) {
	if (T == NULL) return NULL;
	if (key == T->data) return T;
	else if (key < T->data) return FindKey_recursion(T->rchild, key);
	else return FindKey_recursion(T->lchild, key);
}
// 删除指定元素的结点
BSTree DeleteData(BSTree T, TreeType element){
	BSTree parent_p, p, r;
	p = T; parent_p = NULL;
	// 查找找结点位置p 
	while (p != NULL) {
		if (p->data == element) break;
		parent_p = p;
		if (p->data > element) p = p->lchild;
		else p = p->rchild;
	}
	if (p == NULL) return T;
	if (p->lchild == NULL) {
		if (parent_p == NULL) T = p->rchild;
		else if (parent_p->lchild == p) parent_p->lchild = p->lchild;
		else parent_p->rchild = p->rchild;
	}
	else {
		BSTree rr = p;
		for (r = p->rchild; r->lchild != NULL; r = r->lchild) rr = r;
		p->data = r->data;
		if (rr == p)
			p->rchild = r->rchild;
		else rr->lchild = r->rchild;
		p = r;
	}
	free(p);
	return T; // 若删除成功则返回该结点，否则返回NULL
}

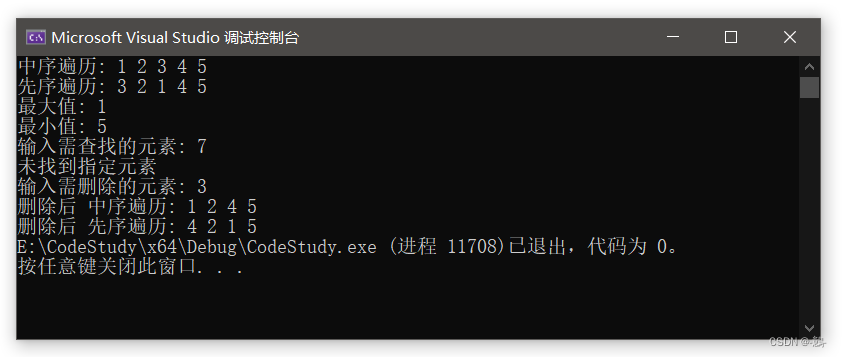
四、运行结果

        main方法代码如下：

int main() {
	TreeType a[] = { 3, 2, 4, 5, 1 };
	BSTree T = NULL;
	for (int i = 0; i < 5; i++) 
		T = InsertTree(a[i], T);

	printf("中序遍历: ");	InOrder(T);
	printf("\n先序遍历: ");	PreOrder(T);

	BSTree p = FindMin(T);
	if (p) 	printf("\n最大值: %d", p->data);
	else 	printf("\n未找到最大值");

	BSTree q = FindMax(T);
	if (q) 	printf("\n最小值: %d", q->data);
	else 	printf("\n未找到最小值");

	int find_data;
	printf("\n输入需查找的元素: ");
	scanf("%d", &find_data);
	p = FindKey_nonrecursion(T, find_data);
	if (p)	printf("找到指定元素: %d", p->data);
	else	printf("未找到指定元素");

	int delete_data;
	printf("\n输入需删除的元素: ");
	scanf("%d", &delete_data);
	BSTree r = DeleteData(T, delete_data);
	printf("删除后 中序遍历: "); InOrder(T);
	printf("\n删除后 先序遍历: "); PreOrder(T);
}

        运行结果如下：

 

五、源代码

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

/* 二叉排序树 */
typedef int TreeType;
typedef struct BSTNode {
	TreeType data;
	struct BSTNode* lchild, * rchild;
}*BSTree, BSTNode;

BSTNode* CreateTreeNode(TreeType data); // 创建二叉树结点
BSTNode* InsertTree(TreeType data, BSTree root); // 插入元素
void PreOrder(BSTree T); // 先序遍历
void InOrder(BSTree T);	 // 中序遍历
BSTree FindMin(BSTree T);  // 查找最小值，返回该结点
BSTree FindMax(BSTree T);  // 查找最大值，返回该结点
BSTree FindKey_nonrecursion(BSTree T, TreeType key);	// 查找指定数据元素(非递归)
BSTree FindKey_recursion(BSTree T, TreeType key);		// 查找指定数据元素(递归)
BSTree DeleteData(BSTree T, TreeType element);			// 删除指定元素的结点

// 创建二叉树结点
BSTNode* CreateTreeNode(TreeType data) {
	BSTNode* p = (BSTNode*)malloc(sizeof(struct BSTNode));
	p->lchild = p->rchild = NULL;
	p->data = data;
	return p;
}
// 插入元素
BSTNode* InsertTree(TreeType data, BSTree root){
	if (root == NULL) {
		root = CreateTreeNode(data);
		return root;
	}
	if (data < root->data)
		root->lchild = InsertTree(data, root->lchild);
	if (data > root->data)
		root->rchild = InsertTree(data, root->rchild);
	return root;
}
// 先序遍历
void PreOrder(BSTree T){
	if (T == NULL) return;
	printf("%d ", T->data);
	PreOrder(T->lchild);
	PreOrder(T->rchild);
}
// 中序遍历
void InOrder(BSTree T){
	if (T == NULL) return;
	InOrder(T->lchild);
	printf("%d ", T->data);
	InOrder(T->rchild);
}
// 查找最小值，返回该结点
BSTree FindMin(BSTree T){
	if (T == NULL) return NULL;
	BSTree min = T;
	while (min->lchild != NULL)
		min = min->lchild;
	return min;
}
// 查找最大值，返回该结点
BSTree FindMax(BSTree T){
	if (T == NULL) return NULL;
	BSTree max = T;
	while (max->rchild != NULL)
		max = max->rchild;
	return max;
}
// 查找指定数据元素(非递归)
BSTree FindKey_nonrecursion(BSTree T, TreeType key) {
	while (T != NULL && key != T->data) {
		if (T->data > key) T = T->lchild;
		else T = T->rchild;
	}
	return T;
}
// 查找指定数据元素(递归)
BSTree FindKey_recursion(BSTree T, TreeType key) {
	if (T == NULL) return NULL;
	if (key == T->data) return T;
	else if (key < T->data) return FindKey_recursion(T->rchild, key);
	else return FindKey_recursion(T->lchild, key);
}
// 删除指定元素的结点
BSTree DeleteData(BSTree T, TreeType element){
	BSTree parent_p, p, r;
	p = T; parent_p = NULL;
	// 查找找结点位置p 
	while (p != NULL) {
		if (p->data == element) break;
		parent_p = p;
		if (p->data > element) p = p->lchild;
		else p = p->rchild;
	}
	if (p == NULL) return T;
	if (p->lchild == NULL) {
		if (parent_p == NULL) T = p->rchild;
		else if (parent_p->lchild == p) parent_p->lchild = p->lchild;
		else parent_p->rchild = p->rchild;
	}
	else {
		BSTree rr = p;
		for (r = p->rchild; r->lchild != NULL; r = r->lchild) rr = r;
		p->data = r->data;
		if (rr == p)
			p->rchild = r->rchild;
		else rr->lchild = r->rchild;
		p = r;
	}
	free(p);
	return T; // 若删除成功则返回该结点，否则返回NULL
}

int main() {
	TreeType a[] = { 3, 2, 4, 5, 1 };
	BSTree T = NULL;
	for (int i = 0; i < 5; i++) 
		T = InsertTree(a[i], T);

	printf("中序遍历: ");	InOrder(T);
	printf("\n先序遍历: ");	PreOrder(T);

	BSTree p = FindMin(T);
	if (p) 	printf("\n最大值: %d", p->data);
	else 	printf("\n未找到最大值");

	BSTree q = FindMax(T);
	if (q) 	printf("\n最小值: %d", q->data);
	else 	printf("\n未找到最小值");

	int find_data;
	printf("\n输入需查找的元素: ");
	scanf("%d", &find_data);
	p = FindKey_nonrecursion(T, find_data);
	if (p)	printf("找到指定元素: %d", p->data);
	else	printf("未找到指定元素");

	int delete_data;
	printf("\n输入需删除的元素: ");
	scanf("%d", &delete_data);
	BSTree r = DeleteData(T, delete_data);
	printf("删除后 中序遍历: "); InOrder(T);
	printf("\n删除后 先序遍历: "); PreOrder(T);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/720459.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Vulnhub靶机PWNLAB：INIT writeup

Vulnhub靶机PWNLAB：INIT writeup

靶机介绍 靶机下载&#xff1a;https://www.vulnhub.com/entry/matrix-2,279/ ​ 个人微信公众号&#xff1a;网络安全学习爱好者 信息搜集 arp扫描存活主机 ​​​ 根据MAC地址比较靶机IP为​192.168.30.131 ​​ nmap扫描全端口及端口服、版本 ​​​ 目录扫描123…
阅读更多...
通信相关知识(三) 接入网

通信相关知识(三) 接入网

接入网的定界 接入网的功能 用户口功能、业务口功能、核心功能、传送功能、接入网系统管理功能。 ADSL 非对称数字用户线路&#xff08;ADSL&#xff0c;Asymmetric Digital Subscriber Line&#xff09;是数字用户线路&#xff08;xDSL&#xff0c;Digital Subscriber Lin…
阅读更多...
【Java从入门到大牛】Java基础语法

【Java从入门到大牛】Java基础语法

&#x1f525; 本文由 程序喵正在路上 原创&#xff0c;CSDN首发&#xff01; &#x1f496; 系列专栏&#xff1a;Java从入门到大牛 &#x1f320; 首发时间&#xff1a;2023年7月5日 &#x1f98b; 欢迎关注&#x1f5b1;点赞&#x1f44d;收藏&#x1f31f;留言&#x1f43e…
阅读更多...
黑客（自学笔记）

黑客（自学笔记）

黑客&#xff0c;对很多人来说充满诱惑力。很多人可以发现这门领域如同任何一门领域&#xff0c;越深入越敬畏&#xff0c;知识如海洋&#xff0c;黑客也存在一些等级&#xff0c;参考知道创宇 CEO ic&#xff08;世界顶级黑客团队 0x557 成员&#xff09;的分享如下&#xff1…
阅读更多...
第一章：项目架构演变

第一章：项目架构演变

1、在设计系统时&#xff0c;应该多思考 墨菲定律 1. 任何事都没有表面上看起来那么简单。 2. 所有的事做起来都会比你预计的时间长。 3. 可能出错的事总会出错。 4. 如果你担心某种情况发生&#xff0c;那么它就更有可能发生。 2、在划分时&#xff0c;也要思考康威定律。…
阅读更多...
centos7安装zookeeper的环境变量配置导致用户登录不了系统

centos7安装zookeeper的环境变量配置导致用户登录不了系统

废话不多说&#xff0c;我修改的/etc/profile,如果这个文件改错会造成所有用户都登录不了系统。 第一步&#xff1a;解决进不了系统 1.在登陆界面按&#xff1a;alt ctrlf2进入命令模式&#xff0c;输入密码登录后再输入&#xff1a; /usr/bin/sudo /usr/bin/vi /etc/profile …
阅读更多...
Apache Doris 在拈花云科的统一数据中台实践，One Size Fits All

Apache Doris 在拈花云科的统一数据中台实践，One Size Fits All

作者&#xff5c;NearFar X Lab 团队 洪守伟、陈超、周志银、左益、武超 整理&#xff5c;SelectDB 内容团队 导读&#xff1a; 无锡拈花云科技服务有限公司&#xff08;以下简称拈花云科&#xff09;是由中国创意文旅集成商拈花湾文旅和北京滴普科技有限公司共同孵化组建的。…
阅读更多...
微信小程序Vant组件配置及使用

微信小程序Vant组件配置及使用

Vant Weapp 官网文档&#xff1a;介绍 - Vant Weapp (gitee.io) Vant Weapp GitHub地址&#xff1a;youzan/vant-weapp: 轻量、可靠的小程序 UI 组件库 (github.com) 本教程使用下载代码方式引入vant组件 1. 下载vant组件源码 通过git下载vant源码 git clone https://github…
阅读更多...
【适配器模式】—— 每天一点小知识

【适配器模式】—— 每天一点小知识

&#x1f4a7; 适配器模式 \color{#FF1493}{适配器模式} 适配器模式&#x1f4a7; &#x1f337; 仰望天空&#xff0c;妳我亦是行人.✨ &#x1f984; 个人主页——微风撞见云的博客&#x1f390; &#x1f433; 《数据结构与算法》专栏的文章图文并茂&#x1f995;…
阅读更多...
Kafka学习笔记（基础篇）

Kafka学习笔记（基础篇）

目录 Kafka简介 消息队列 Kafka的应用场景 消息队列的两种模型 Kafka集群搭建 Kafka的生产者/消费者/工具 Kafka的基准测试工具 Kafka Java API开发 生产者程序开发 消费者程序开发 生产者使用异步方式生产消息 Kafka中的重要概念 消费者组 幂等性 事务编程 Ka…
阅读更多...
英文单词的3σ值

英文单词的3σ值

最近做log的nlp&#xff0c;发现日志当中有一些很长的但是无意义的词汇&#xff0c;很影响训练模型&#xff0c;这边想通过单次长度去排除那些无意义词汇&#xff0c;去查了gpt英文单次的3σ值&#xff0c;记录下
阅读更多...
谷歌浏览器中的谷歌翻译失效了？如何解决谷歌翻译不响应问题？

谷歌浏览器中的谷歌翻译失效了？如何解决谷歌翻译不响应问题？

1 原因分析 因为谷歌把国内的服务器关了。 2 下载软件 &#xff08;1&#xff09;Mac OS https://github.com/Ponderfly/GoogleTranslateIpCheck/releases/download/1.6/GoogleTranslateIpCheck-mac-x64.zip&#xff08;2&#xff09;Windows https://github.com/Ponderfl…
阅读更多...
【MySQL体系结构及CetOS7安装MySQL和修改密码】

【MySQL体系结构及CetOS7安装MySQL和修改密码】

MySQL体系结构及安装MySQL MySQL体系结构CentOS7安装MySQL四种方法1、离线安装2、在线安装3、通用二级制方式4、容器方式安装 设置及修改密码忘记密码恢复 MySQL体系结构 MySQL是一种常用的关系型数据库管理系统&#xff08;RDBMS&#xff09;&#xff0c;其体系结构包括以下&…
阅读更多...
ARM架构（ARM汇编指令练习）

ARM架构（ARM汇编指令练习）

文章目录 前言一、MOV指令二、内存访问指令1.LDR指令2.STR指令 三、数据处理指令1.ADD指令2.SUB指令3.位操作指令4.CMP指令 四、跳转指令总结 前言 本篇文章带大家来学习ARM汇编的一些常用的指令&#xff0c;这里指令都是非常基础的指令。 一、MOV指令 MOV&#xff08;Move&…
阅读更多...
一个 Kill 不掉的 MySQL 会话

一个 Kill 不掉的 MySQL 会话

究竟是什么原因&#xff0c;导致主从切换过程中存在一个无法 kill 的会话&#xff1f; 作者&#xff1a;秦广飞 爱可生 DBA 团队成员&#xff0c;负责项目日常问题处理及公司平台问题排查&#xff0c;对数据库有兴趣&#xff0c;对技术有想法。一入 IT 深似海&#xff0c;从此节…
阅读更多...
【钱处理】商业计算怎样才能保证精度不丢失

【钱处理】商业计算怎样才能保证精度不丢失

以项目驱动学习&#xff0c;以实践检验真知 前言 很多系统都有「处理金额」的需求&#xff0c;比如电商系统、财务系统、收银系统&#xff0c;等等。只要和钱扯上关系&#xff0c;就不得不打起十二万分精神来对待&#xff0c;一分一毫都不能出错&#xff0c;否则对系统和用户来…
阅读更多...
集群 第一章

集群 第一章

目录 1.群集的含义 2.群集分类 3.群集架构 4.负载调度工作模式 5.lvs 虚拟服务器 6.nat 模式 lvs 负载均衡群集部署 7.总结 1.群集的含义 由多台主机构成&#xff0c;但对外只表现为一个整体&#xff0c;只提供一个访问入口&#xff08;域名与IP地址&#xff09;&#…
阅读更多...
建筑师们，你们该把三维模型弄到PPT里做汇报了！

建筑师们，你们该把三维模型弄到PPT里做汇报了！

➤如何实现项目汇报效率比传统的PPT高&#xff0c;同时汇报效果更直观&#xff1f; ➤如何摆脱方案汇报只能向客户交付数据&#xff0c;安装专业软件查看项目成果&#xff1f; ➤如何将无人机航测数据、CAD图纸、BIM设计成果进行融合&#xff0c;挖掘出更深层次的应用&#x…
阅读更多...
mysql体系结构及安装部署mysql

mysql体系结构及安装部署mysql

目录 1.体系结构 2.安装mysql 1.yum 源安装 2. 第二种安装方式-通用二进制方式 3.mysql改密方式 第一种&#xff0c;知道密码的情况下 第二种&#xff0c;不知道密码 1.体系结构 MySQL server连接层连接池&#xff08;缓冲池&#xff09;SQL层系统管理和控制工具SQL…
阅读更多...
亿级日活业务稳如磐石 华为云发布性能测试服务CodeArts PerfTest

亿级日活业务稳如磐石 华为云发布性能测试服务CodeArts PerfTest

HDC期间可参与华为云PaaS生态抽奖活动&#xff0c;活动链接在文末 计算机软件作为人类逻辑智慧的伟大结晶之一&#xff0c;已经渗透到了人类社会的各个角落。早期的计算机发展对硬件有很强的依赖性&#xff0c;只有少数的个人或者机构才能拥有软件这种“奢侈品”。但随着软件行…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023