笔者说：我们为什么要学记忆化搜索？

因为——有些动态规划直接去想递推公式太难了，所以可以先写成记忆化搜索。

由于记忆化搜索是从将大问题分解成子问题的角度去考虑的，所以会简单一些。

本文的题目其实都比较简单，但是为了学习记忆化搜索，还是要用记忆化搜索再做一遍，不要眼高手低。

如果读者觉得本文的题目太简单了，可以去尝试一下【算法】区间DP （从记忆化搜索到递推DP）⭐ 这篇文章中的题目。

下面主要就是题单，本文没什么好看好学的。

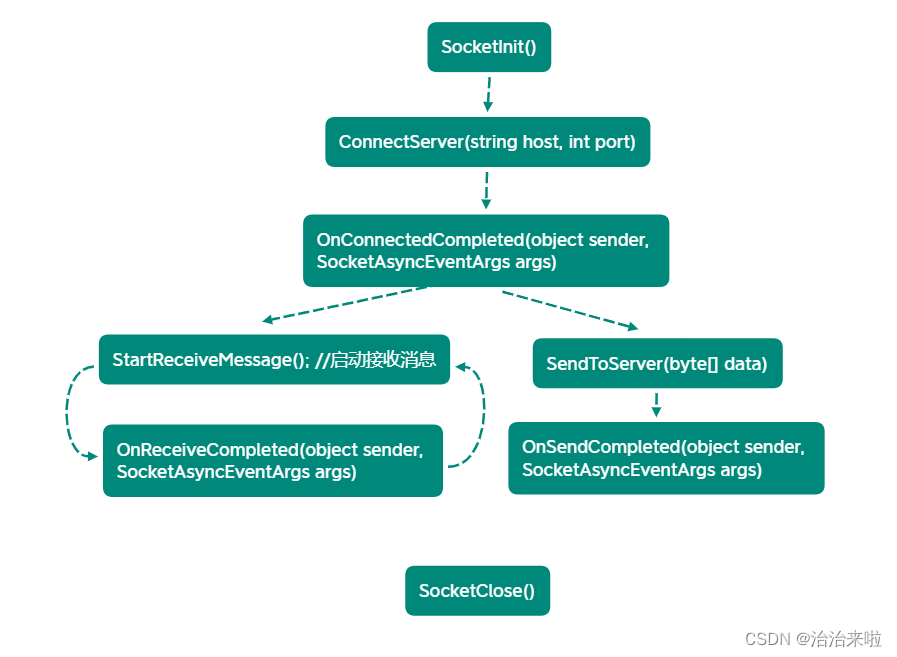
预备知识

在这里插入图片描述
就像图中写的一样，先思考回溯要怎么写，然后改成记忆化搜索，然后将这个版本的代码翻译成递推公式形式的 dp。

例题：198. 打家劫舍

198. 打家劫舍

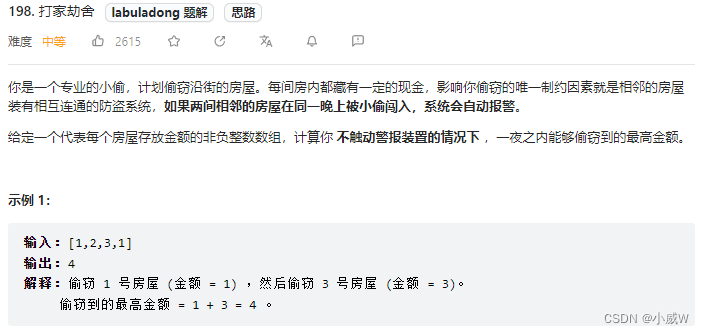
在这里插入图片描述
提示：

1 <= nums.length <= 100
0 <= nums[i] <= 400

记忆化搜索

在这里插入图片描述

将大问题分解成子问题，即 dfs (i) 可以分解成 dfs (i - 1)

class Solution {
    int[] nums, memo;
    int ans = 0;

    public int rob(int[] nums) {
        this.nums = nums;
        memo = new int[nums.length];
        Arrays.fill(memo, -1);
        return dfs(0);
    }

    public int dfs(int i) {
        if (i >= nums.length) return 0;
        if (memo[i] != -1) return memo[i];
        memo[i] = Math.max(nums[i] + dfs(i + 2), dfs(i + 1));
        return memo[i];
    }
}

翻译成 dp 如下：

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if (n == 1) return nums[0];
        int[] dp = new int[n];
        dp[0] = nums[0];
        dp[1] = Math.max(dp[0], nums[1]);
        for (int i = 2; i < n; ++i) dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
        return Math.max(dp[n - 1], dp[n - 2]);
    }
}

由于 dp 数组的无后效性，因此还可以将 dp 数组优化成两个变量。（这里就不写了

相关题目练习

70. 爬楼梯

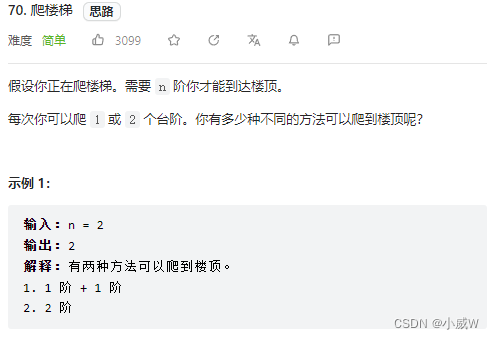
在这里插入图片描述

记忆化搜索

class Solution {
    int[] memo;
    int n;

    public int climbStairs(int n) {
        this.n = n;
        memo = new int[n + 1];
        Arrays.fill(memo, -1);
        return dfs(n);
    }

    public int dfs(int i) {
        if (i <= 2) return i;
        if (memo[i] != -1) return memo[i];
        return memo[i] = dfs(i - 1) + dfs(i - 2);
    }
}

dp

class Solution {
    public int climbStairs(int n) {
        if (n == 1 || n == 2) return n;
        int[] dp = new int[n];
        dp[0] = 1;
        dp[1] = 2;
        for (int i = 2; i < n; ++i) dp[i] += dp[i - 1] + dp[i - 2];
        return dp[n - 1];
    }
}

746. 使用最小花费爬楼梯

746. 使用最小花费爬楼梯
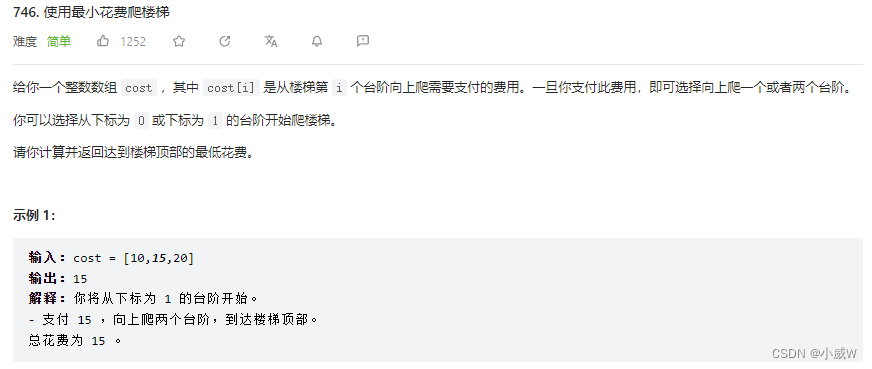
在这里插入图片描述

提示：

2 <= cost.length <= 1000
0 <= cost[i] <= 999

记忆化搜索

class Solution {
    int[] cost, memo;
    int n;

    public int minCostClimbingStairs(int[] cost) {
        this.cost = cost;
        n = cost.length;
        memo = new int[n];
        Arrays.fill(memo, -1);
        return Math.min(dfs(n - 1), dfs(n - 2));    // dfs(i)表示从i再走一步需要的花费
    }

    public int dfs(int i) {
        if (i < 0) return 0;
        if (memo[i] != -1) return memo[i];
        return memo[i] = cost[i] + Math.min(dfs(i - 1), dfs(i - 2));
    }
}

dp

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int[] dp = new int[n];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for (int i = 2; i < n; ++i) dp[i] = Math.min(dp[i - 2], dp[i - 1]) + cost[i];
        return Math.min(dp[n - 1], dp[n - 2]);
    }
}

2466. 统计构造好字符串的方案数

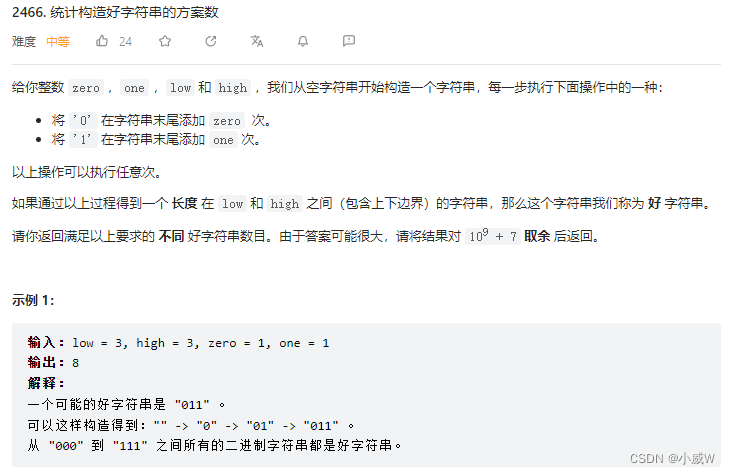
在这里插入图片描述

记忆化搜索

class Solution {
    final long MOD = (long)1e9 + 7;
    long[] memo;
    int zero, one;

    public int countGoodStrings(int low, int high, int zero, int one) {
        this.zero = zero;
        this.one = one;
        memo = new long[high + 1];
        Arrays.fill(memo, -1);
        long ans = 0;
        for (int i = low; i <= high; ++i) ans = (ans + dfs(i)) % MOD;
        return (int)ans;
    }

    public long dfs(int i) {
        if (i == 0) return 1;
        if (i < 0) return 0;
        if (memo[i] != -1) return memo[i];
        return memo[i] = (dfs(i - zero) + dfs(i - one)) % MOD;
    }
}

dp

class Solution {
    public int countGoodStrings(int low, int high, int zero, int one) {
        long[] dp = new long[high + 1];
        dp[0] = 1;
        final long MOD = (long)1e9 + 7;
        long ans = 0;

        for (int i = 1; i <= high; ++i) {
            dp[i] = (dp[i] + (i - zero >= 0? dp[i -zero]: 0)) % MOD;
            dp[i] = (dp[i] + (i - one >= 0? dp[i -one]: 0)) % MOD;
            if (i >= low) ans = (ans + dp[i]) % MOD;
        }
        return (int)ans;
    }
}

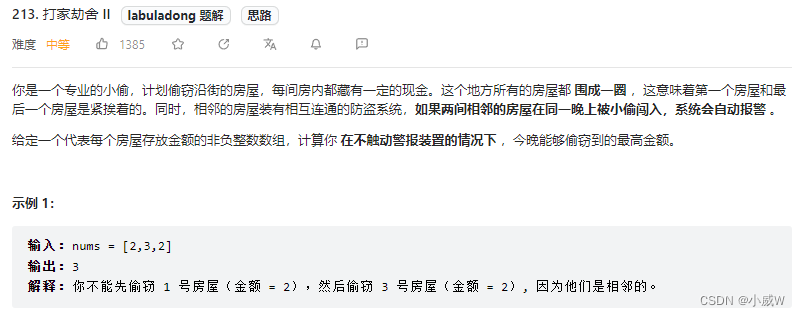
213. 打家劫舍 II

在这里插入图片描述

记忆化搜索

class Solution:
    def rob(self, nums: List[int]) -> int:
        # 防止一些题目爆栈
        sys.setrecursionlimit(10000000)
        # 在3.9以前的版本没有@cache可使用@lru_cache(maxsize=None)达成一样的效果
        # 当然这里也可以用哈希表手动存
        @cache
        def dfs(i,end,s):
            if i>=end:
                return 0
            if not s:
                return max(dfs(i+1,end,True)+nums[i],dfs(i+1,end,False))
            return dfs(i+1,end,False)
        return max(dfs(1,len(nums)-1,True)+nums[0],dfs(1,len(nums),False))

dp

不偷0，或者不偷n-1

class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if (n == 1) return nums[0];
        int[][] dp = new int[n][2];
        dp[0][0] = nums[0];
        dp[1][0] = Math.max(nums[0], nums[1]);
        dp[1][1] = nums[1];
        for (int i = 2; i < n; ++i) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 2][0] + nums[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][1] + nums[i]);
        }
        return Math.max(dp[n - 2][0], dp[n - 1][1]);
    }
}