个人主页:平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望对大家有所帮助
🍓希望我们一起努力、成长,共同进步。
点击直接跳转到该题目
目录
- 题目描述🥪
- 算法原理🍔
- 代码实现🧀
- 代码优化+代码实现🥖
题目描述🥪


算法原理🍔
状态表示:
根据以往做题的经验和,题目描述,我们可以以某个位置为起点或者以某个位置为终点进行分析问题。
根据题目要求,状态表示以i位置为结尾dp[i]表示以i位置为结尾时,解码方法的总数。
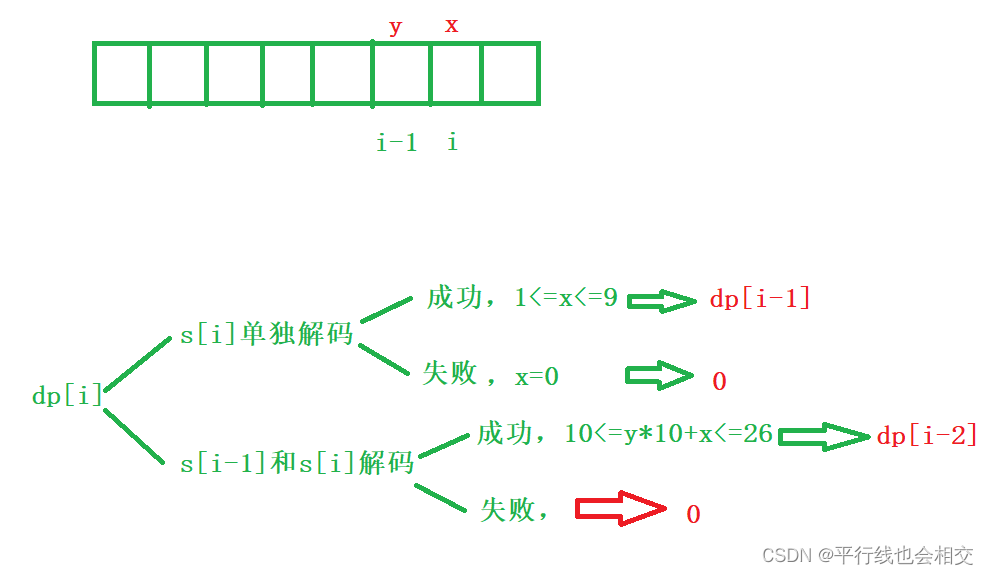
状态转移方程:
根据以往的经验,我们依然是根据最近的状态来划分问题。
状态转移方程:dp[i]=dp[i-1]+dp[i-2]。
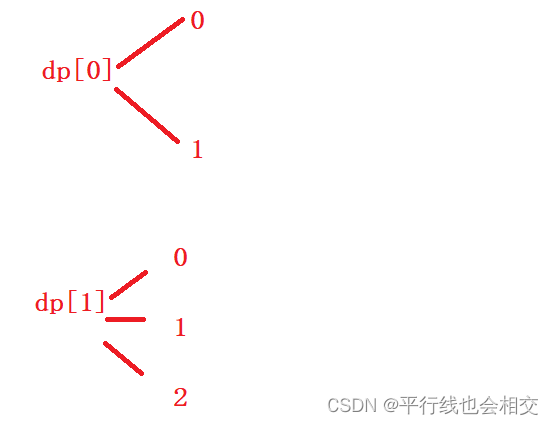
初始化:
为了防止越界问题,所以这里我们对
dp[0]和dp[1]进行初始化。
填表顺序:
综上所述,填表顺序是从左往右进行的。
返回值:
根据题意,我们要求的是整个字符串进行解码的方案的总数,也就是说我们需要解码到最后一个位置才可以。由于最后一个位置是
n-1,所以我们最后返回的是dp[n-1]
代码实现🧀
在编写代码时,依然是按照之前的步骤来进行代码的编写,即创建dp表、初始化、填表、返回值。
class Solution {
public:
int numDecodings(string s) {
int n = s.size();
vector<int> dp(n);
dp[0] = s[0] != '0';
//处理边界情况
if(n==1) return dp[0];
if(s[0]!='0'&&s[1]!='0') dp[1] += 1;
int tmp = (s[0]-'0')*10 + (s[1]-'0');
if(tmp>=10&&tmp<=26) dp[1] += 1;
for(int i = 2;i < n;i++)
{
if(s[i]!='0') dp[i] += dp[i-1];//处理单独编码的情况
int tmp = (s[i-1]-'0')*10 + (s[i]-'0');//处理第二种情况
if(tmp>=10&&tmp<=26) dp[i]+=dp[i-2];
}
return dp[n-1];
}
};
代码优化+代码实现🥖
在动态规划dp问题中,我们会经常碰到繁琐的处理边界问题的情况以及初始化问题。所以这里有一个处理边界问题以及初始化的技巧:我们在创建dp表的时候多开一个元素位置的空间。我们把新dp表中的d[0]称之为虚拟节点。
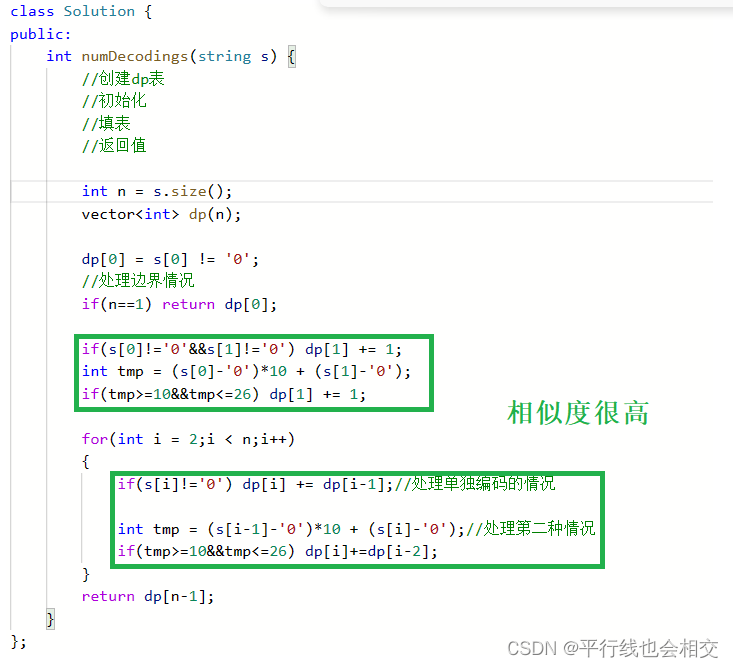
我们可以看到上述解题代码初始化部分和填表部分代码的相似度有一点高。我们可以将初始化部分的代码放到填表部分来解决这种代码相似度比较高的情况。
在原先的解题代码中我们在初始化dp[1]的时候是最麻烦的,而现在由于我们在创建dp表的时候多开辟了一块空间,所以我们只需要对新dp表中的
dp[0]和dp[1]进行初始化即可,此时就把原dp表中的dp[1]的初始化转换为填表的逻辑中(相当于把原来dp[1]的初始化去掉了,直接在新dp表中填表即可)。
如果想要保证后面的填表时正确呢?请看:
1.虚拟节点(即新dp表中的dp[0])中的值要保证后面的填表是正确的。
2.一定要注意下标的映射关系。
这里举一个例子:现在我们要填写新dp表中的dp[2],由于dp[i]=dp[i-1]+dp[i-2],所以我们需要dp[0]和dp[1]的值,而dp[1]中的值和原dp表中的dp[0]的求取逻辑是一模一样的,所以现在我们只需要关心新dp表中dp[0]应该怎样初始化。这里一般情况下dp[0]这里是要初始化成0。但是根据本题的题目要求,dp[0]并不能初始化成0,而是初始化成1。
现在来解释为什么新dp表中的dp[0]不能初始化为0
还是以新dp表中dp[2]的位置为例,由前面分析得知需要知道新dp表中dp[0]的值,对应的原字符串s[0]和s[1]拼起来后可以解码成功,既然解码成功了,所以就需要加上dp[0]的值(即加上1),即找到了一种解码方式,如果我们初始化为0的话,就相当于忽略了这一种解码方式。

请看优化后的解题代码:
class Solution {
public:
int numDecodings(string s) {
int n = s.size();
vector<int> dp(n+1);
dp[0] = 1;
dp[1] = s[1-1]!='0';//与原dp表中dp[0]位置的初始化的逻辑是一样的,这里要注意下标的映射关系
for(int i = 2;i <= n;i++)
{
//注意s字符串的映射关系
if(s[i-1]!='0') dp[i] += dp[i-1];//处理单独编码的情况
int tmp = (s[i-2]-'0')*10 + (s[i-1]-'0');//处理第二种情况
if(tmp>=10&&tmp<=26) dp[i]+=dp[i-2];
}
return dp[n];
}
};
好了,本文就到这里啦!
再见啦,友友们!!!