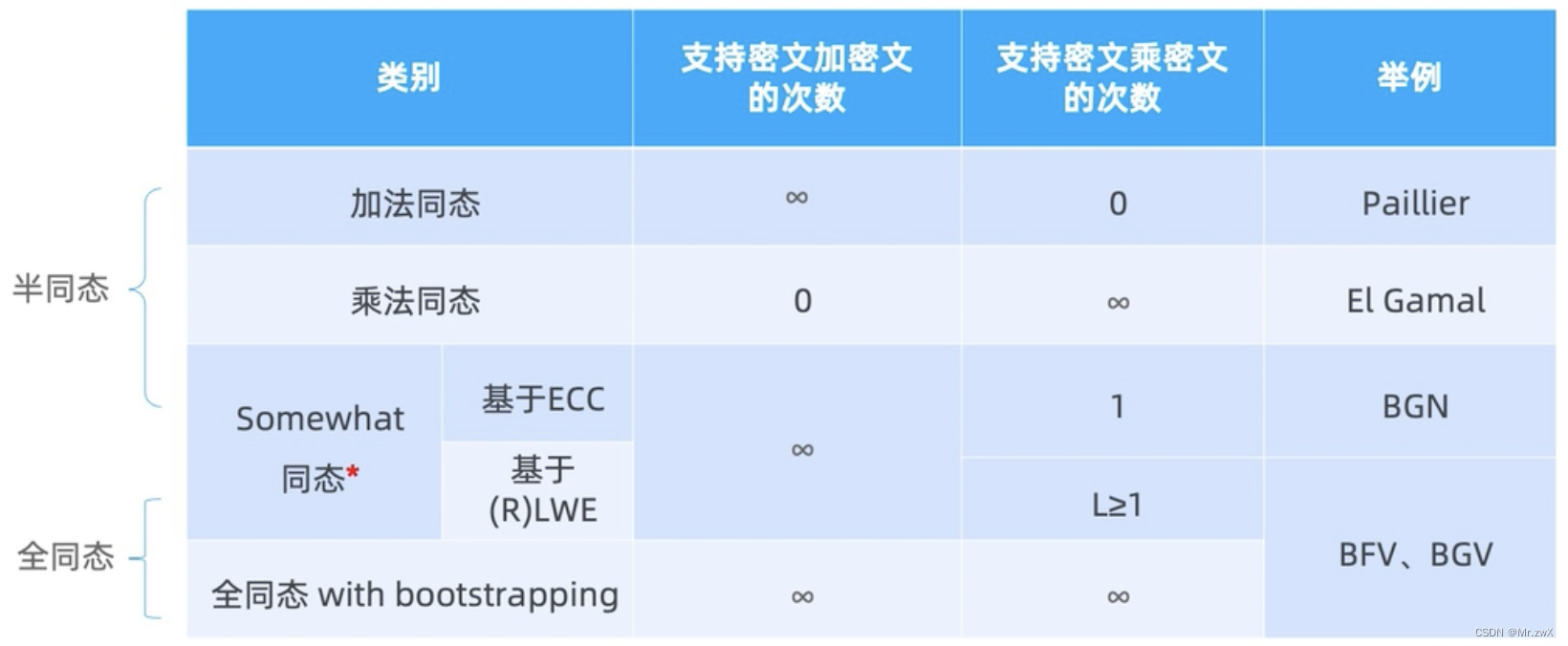
1 半同态加密

定义：只支持乘法或加法中的一种的同态加密。同态加密指的是允许直接对密文进行计算，密文计算结果解密后与明文直接计算结果相同。

Pailliar加法同态加密

Paillier加解密过程

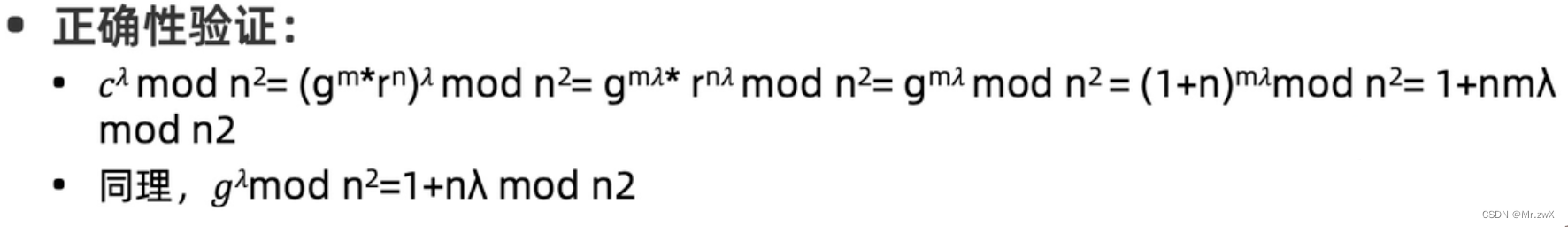
Paillier的同态性

明文加法 <=> 密文乘法
明文乘法 <=> 密文指数幂

Paillier的安全性

基于大整数分解困难问题

El Gamal乘法同态加密

相比Paillier，El Gamal性能更好，但是做加法同态时，解密需要求离散对数，只适用明文较小情况。

RSA乘法同态加密

参考我之前写的RSA算法博客：【密码学基础】RSA加密算法

显然，RSA的加解密都是同指数幂的指数运算，所以满足乘法同态性。

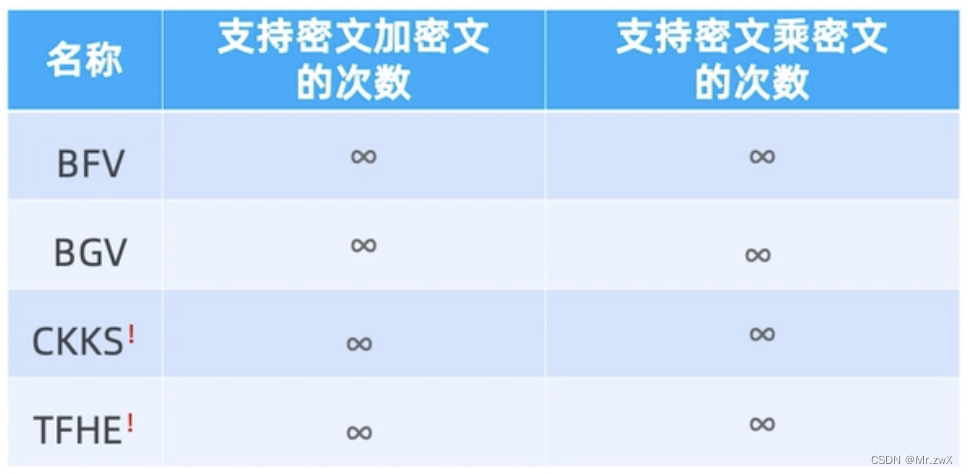
2 全同态加密

定义：能在加密的数据上进行任意数量的加法和乘法运算的加密算法，使得密文计算结果解密后与明文直接计算结果相同。

BFV全同态加密

BFV全同态是基于环上learning with error的算法，同态性是多项式同态，而非数值！所以在明文空间中，如何将原始数值编码到多项式，就很有挑战性了。

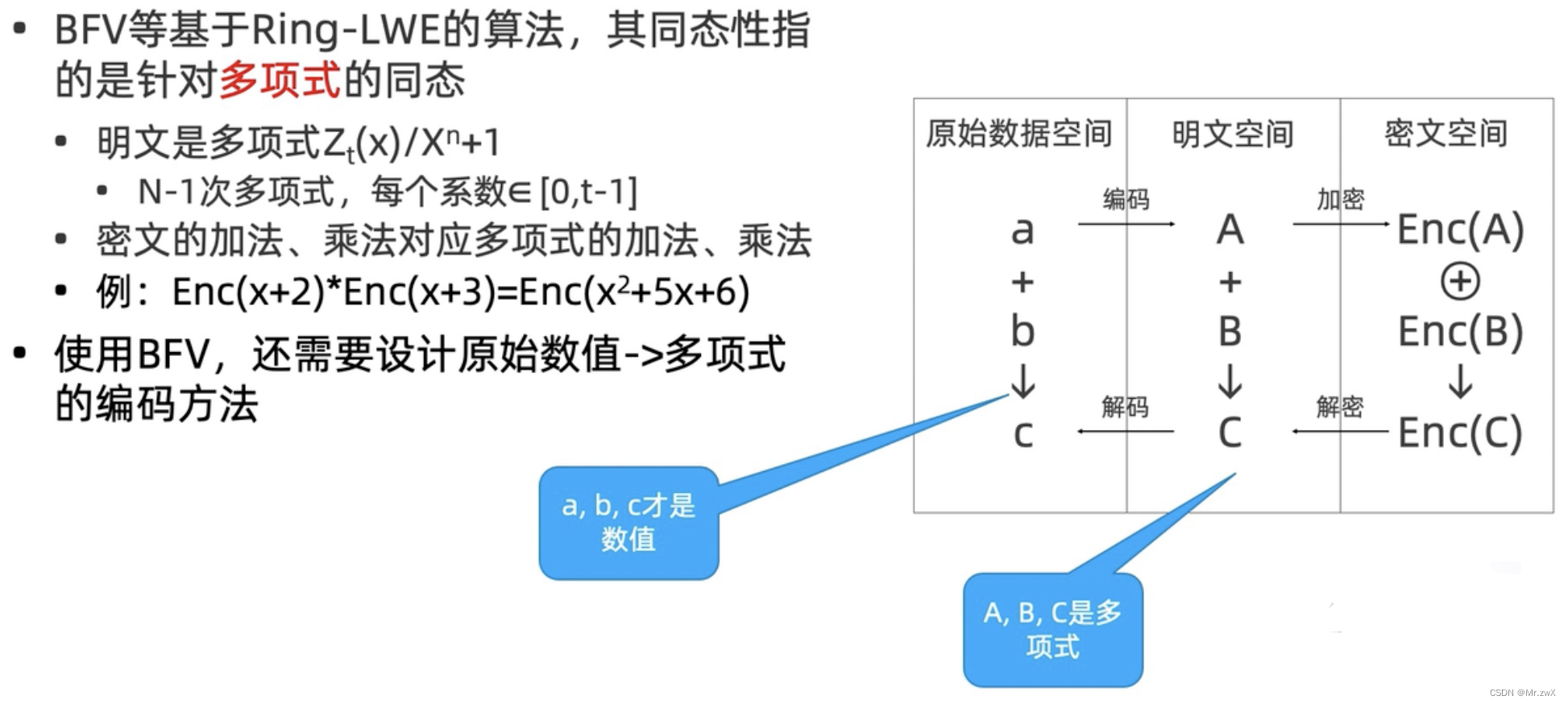
BFV的编码方式

常见的编码方式是SIMD：Single Instruction Multiple Data

多项式的同态性传递到原始数据的同态性。SIMD的优势是能在同一个多项式中打包多个数据。

BFV加解密过程

s是私钥，pk是公钥。随机多项式e是服从高斯分布，大概率是非常小的，所以解密是可以被四舍五入掉（比如示例中的0.15x^2和0.04两项）。

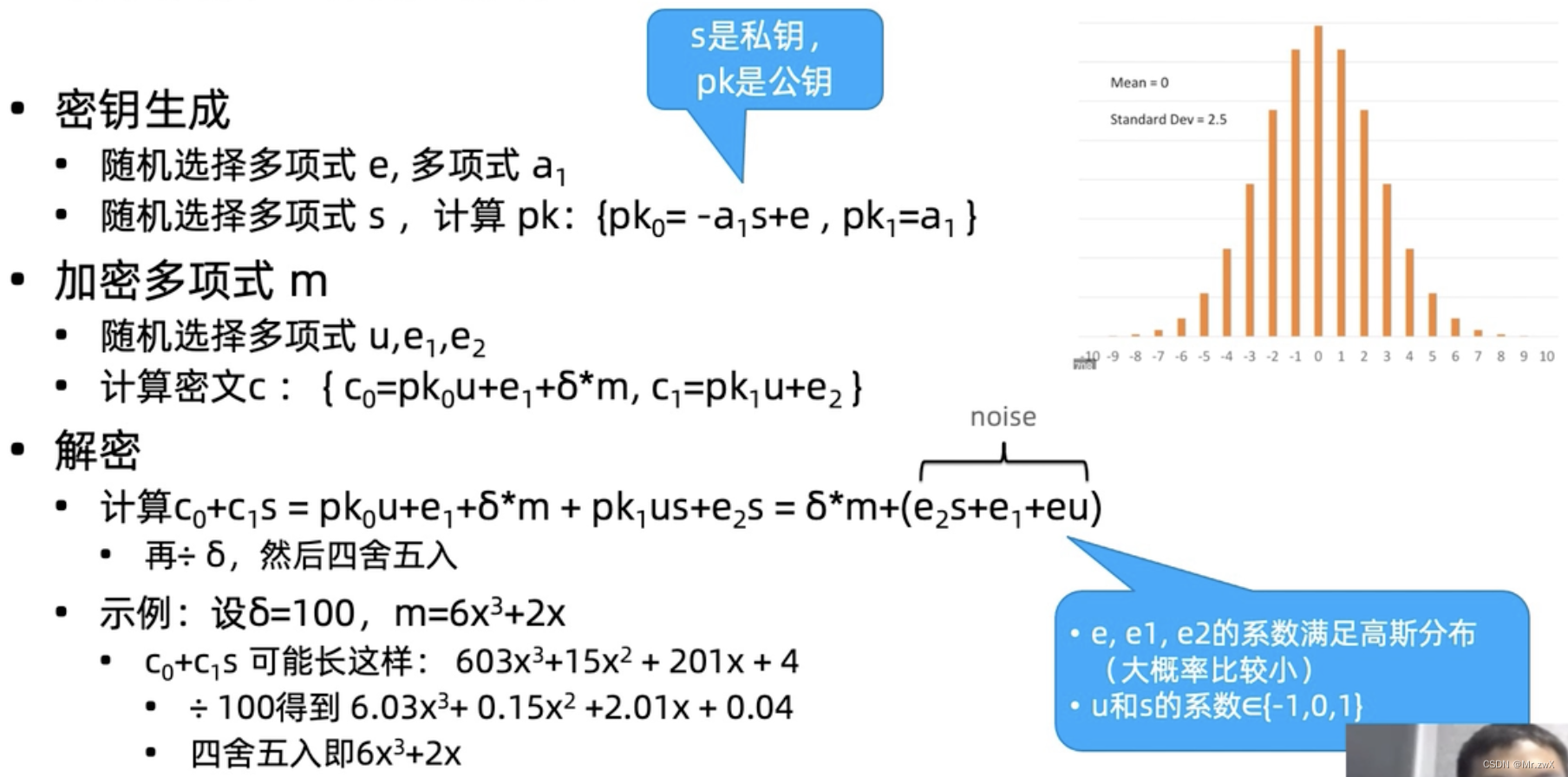
BFV的安全性

基于RLWE困难问题

BFV的同态性

加法同态：

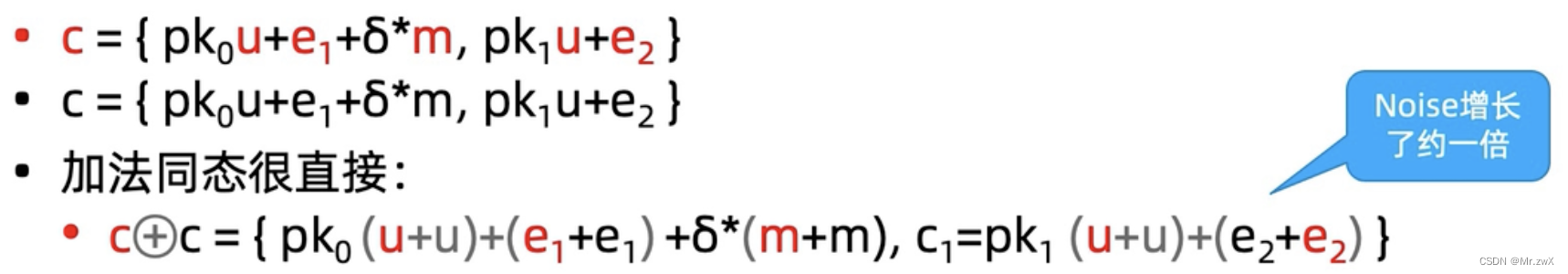
注：每次同态加法导致噪声翻倍。

乘法同态：

注：每次同态乘法导致噪声增长约明文长度倍。
由此可以看到，$\delta$越大，能容忍的噪声就越大！所以决定了乘法的次数（计算深度）。

自举Bootstrapping

前面说到噪声会在同态运算中不断增大，且不能超过$\delta /2$，支持最大乘法次数是L。Bootstrapping则可以让密文满血复活，成为又可以操作L次的密文了。
这个过程就是同态函数D来实现的，D是密文空间中的同态解密算子，即用加密的私钥sk解密密文ct，得到加密的明文Enc(m)，也就是密文ct本身。
本质上，Bootstrapping的过程就是从密文ct到ct的变化，特别之处就是中间存在一步同态解密过程，消除了（累积的）噪声。

3 同态加密应用场景

场景1：安全向量内积

安全向量内积的半同态解决方案：
A用Paillier加密数据a，发送给B与数据b执行密文-明文乘法，然后发给A解密。缺点是性能很低。

安全向量内积的全同态解决方案1:
将向量打包到多项式，执行多项式同态乘法。需要rotation操作！将$a_i{b}_i$都旋转到第一项，然后执行同态加法。但是rotation操作开销很大！

安全向量内积的全同态解决方案2:
对B编码时，调整多项式系数的位置，发现多项式相乘后$a_i{b}_i$就已经在一起了，无需rotation！

总结：编码方式很重要！不同的编码方式性能可能差100倍以上！

场景2：安全数据库

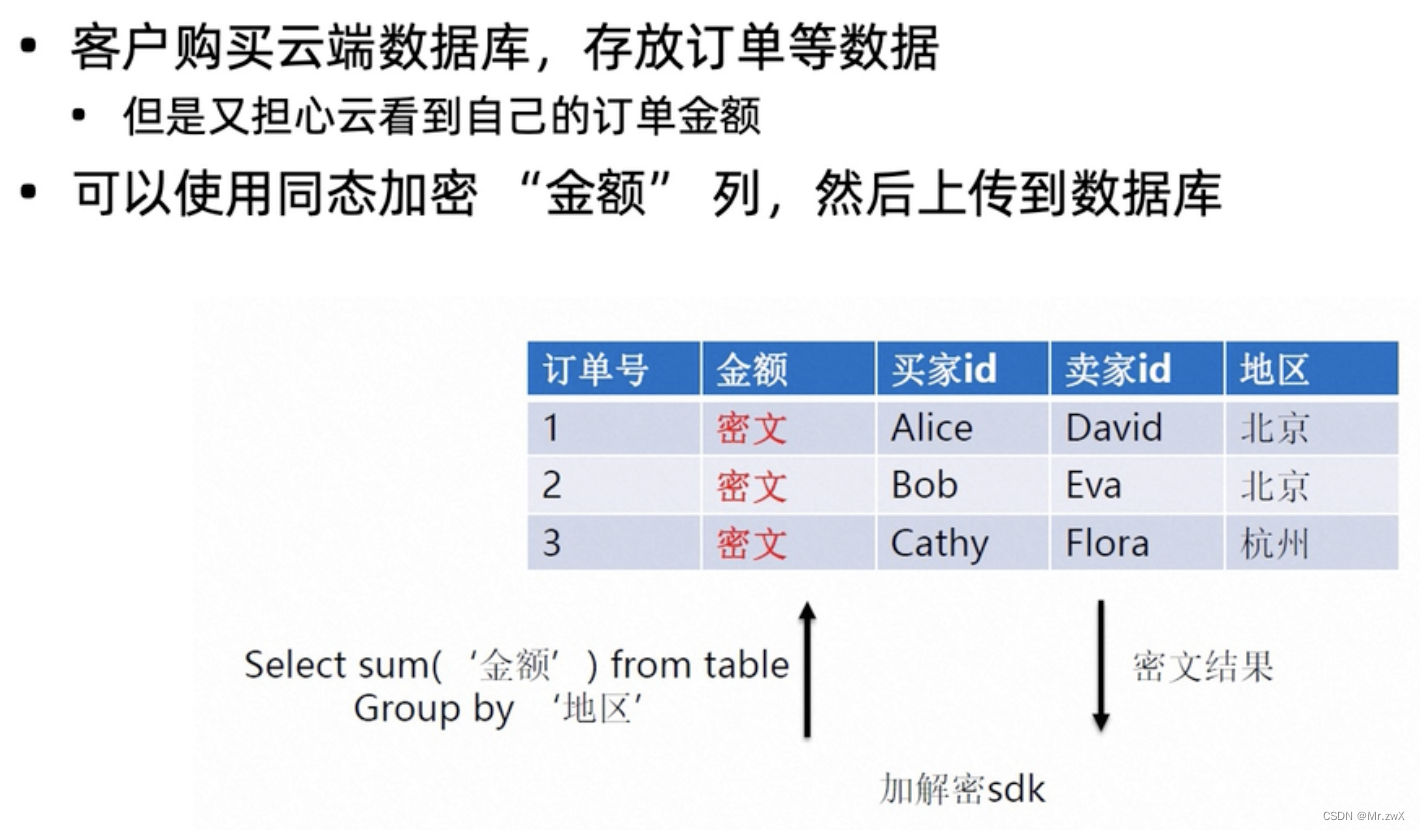
场景3：安全聚合（Secure Aggregation）

在联邦学习中通过同态加密保护梯度，但是需要参与方大于2，否则可以反推梯度。

真正的全同态计算还不实际

技术展望

理论创新

应用创新

硬件加速

参考资料

「隐私计算基础理论」同态加密技术及其应用 - 阿里 洪澄