1.简述

       学习目标：一个图像处理的经典综合案例

一、图像锐化的原理
  图像锐化的目的是凸显物体的细节轮廓，通常可以用梯度、Laplace算子和高通滤波来实现，下面一一说明：

1、梯度法
梯度计算可以参考 小白学习图像处理——canny边缘检测算法 ，假设Gx为x方向的方向导数，Gy为y方向的方向导数，那么梯度就是Gx和Gy的平方和开根号：
G = [ G x 2 + G y 2 ] 2 G = [Gx^2 + Gy^2]^2
G=[Gx 
2
 +Gy 
2
 ] 
2
 

其中，计算Gx和Gy的过程就是用一个预先定义的矩阵和图像做一次二维卷积，我们把这个预先定义的矩阵成为模板算子，计算Gx和Gy的算子有很多种。

二、边缘检测
  在matlab中预置了一些算子，如：roberts、sobel、prewitt、log 和 canny 算子等

1、图像的线段检测
  首先谈谈图像线段的检测，线段检测的原理类似梯度，线段通常具有这样的特点，线段上的灰度与左右两侧的灰度相比更加突出，因为它的灰度要么比两边都大，要么比两边都小，我们可以将像素点的灰度同时和两边灰度进行对比，判断它是否属于某一条边。

 

2.代码

clear;clc;close all
%%   读取图像
I=imread('1.jpg');
try
    I=rgb2gray(I);    %如果是RGB图像，则转化为灰度图
end

%%    添加噪声
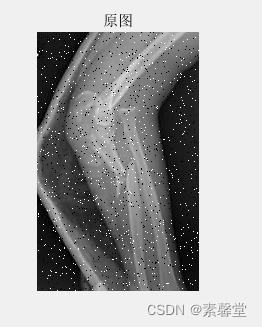
I=imnoise(I,'salt & pepper',0.04);     % 叠加密度为0.04的椒盐噪声
figure
imshow(I)
title('原图')

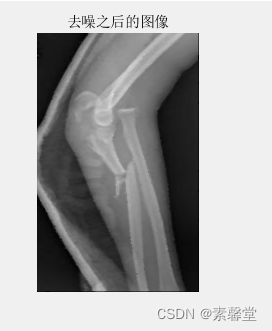
%%   图像去噪
I=medfilt2(I,[2 4]);   %采用二维中值滤波函数对图像滤波
figure
imshow(I)
title('去噪之后的图像')

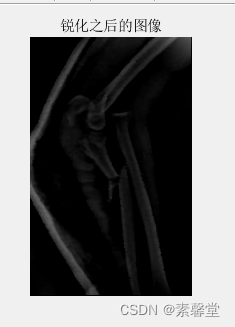
%%   图像锐化
[M,N]=size(I);   % 计算图像尺寸
f=double(I);     % 数据类型转换，MATLAB不支持图像的无符号整型的计算
g=fft2(f);       % 二维傅立叶变换，得到频域信息
g=fftshift(g);   % 0频率移到(M/2,N/2)处

n=2;             % 二阶巴特沃斯滤波器
D0=3;            % 巴特沃斯滤波器的D0，D0越大，保留的高频信号就越少（对于不同的图片，可以自行调节，以便得到好的效果）
for i=1:M
    for j=1:N 
        D=sqrt((i-M/2)^2+(j-N/2)^2);   %计算离0频率(M/2,N/2)的距离
        h=1/(1+(D0/D)^(2*n));          %计算传递函数的值
        output(i,j)=h*g(i,j);          %高通滤波之后(i,j)处的值
    end
end
result=ifftshift(output);              %与g=fftshift(g)对应，还原回去
I=ifft2(result);                       %傅里叶反变换
I=uint8(real(I));                      %得到滤波之后的图像（锐化之后的图像）
figure
imshow(I)                               %滤波后图像显示
title('锐化之后的图像')

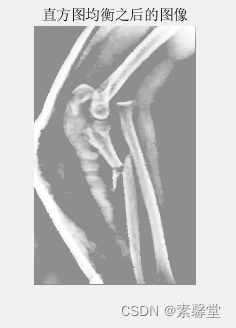
%%   直方图均衡化处理
I=histeq(I);                             %得到直方图均衡化之后的图像
figure
imshow(I)
title('直方图均衡之后的图像')

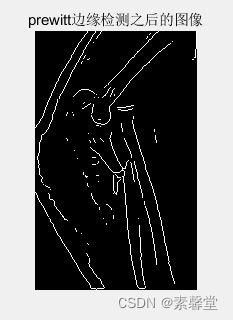
%%   边缘检测
I1=edge(I,'prewitt');
I2=edge(I,'roberts');
I3=edge(I,'sobel');

figure
imshow(I1)
title('prewitt边缘检测之后的图像')

figure
imshow(I2)
title('roberts边缘检测之后的图像')

figure
imshow(I3)
title('sobel边缘检测之后的图像')
 

3.运行结果