二叉树的练习

news2025/11/1 5:12:57

文章目录

  • 单值二叉树
  • 检查两颗树是否相同
  • 对称二叉树
  • 二叉树的前序遍历
  • 二叉树的中序遍历
  • 二叉树的后序遍历
  • 另一颗树的子树
  • 通过前序遍历的数组构建二叉树
  • 判断二叉树是否是完全二叉树
  • 层序遍历
  • k层节点数
  • 二叉树的销毁
  • 二叉树的整体

单值二叉树

单值二叉树，可以使用等式的传递性来解决，根的值和左右子树的值相比较，看是否相等。再比较左右子树。递归求出是否为单值二叉树。
代码如下：

bool isUnivalTree(struct TreeNode* root){
    if(root == NULL)
    {
        return true;
    }
    if(root->left&&root->left->val!=root->val)
    {
        return false;
    }
    if(root->right&&root->right->val!=root->val)
    {
        return false;
    }
    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

检查两颗树是否相同

先比比较根，在比较左右子树。

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    if(p==NULL||q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}

对称二叉树

先比较根的左右子树的根。在比较左子树的左和右子树的右，左子树的右和右子树的左

bool _isSymmetric(struct TreeNode* RootLeft,struct TreeNode* RootRight)
{
    if(RootLeft == NULL&&RootRight == NULL)
    {
        return true;
    }
    if(RootLeft == NULL ||RootRight == NULL)
    {
        return false;
    }
    if(RootLeft->val != RootRight ->val)
    {
        return false;
    }
    return _isSymmetric(RootLeft->left,RootRight->right) && 
    _isSymmetric(RootLeft->right,RootRight->left);
}
bool isSymmetric(struct TreeNode* root){
    return _isSymmetric(root->left,root->right);
}

二叉树的前序遍历

前序遍历到数组中，注意下标的传值要使用传址调用

int BTreeSize(struct TreeNode* root)
{
  if(root == NULL)
  {
    return 0;
  }
  int lcount = BTreeSize(root->left);
  int rcount = BTreeSize(root-> right);
  return lcount + rcount + 1;
  
}
void _preorderTraversal(struct TreeNode* root,int* a,int* i)
{
  if(root==NULL)
  {
    return;
  }
  a[(*i)++] = root->val;
  _preorderTraversal(root->left,a,i);
  _preorderTraversal(root->right,a,i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
    *returnSize = BTreeSize(root);
    //malloc一个数组
    int* a = (int*)malloc(sizeof(int)*(*returnSize));
    //执行前序遍历
    //下标
    int i  = 0;
    _preorderTraversal(root,a,&i);
    return a;
}

二叉树的中序遍历

调换这几条语句的顺序
a[(*i)++] = root->val; _preorderTraversal(root->left,a,i); _preorderTraversal(root->right,a,i);
函数名要保证和对应的遍历相同

 int BTreeSize(struct TreeNode* root)
{
  if(root == NULL)
  {
    return 0;
  }
  int lcount = BTreeSize(root->left);
  int rcount = BTreeSize(root-> right);
  return lcount + rcount + 1;
  
}
void _inorderTraversal(struct TreeNode* root,int* a,int* i)
{
  if(root==NULL)
  {
    return;
  }
 
  _inorderTraversal(root->left,a,i);
   a[(*i)++] = root->val;
  _inorderTraversal(root->right,a,i);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
    *returnSize = BTreeSize(root);
    //malloc一个数组
    int* a = (int*)malloc(sizeof(int)*(*returnSize));
    //执行前序遍历
    //下标
    int i  = 0;
    _inorderTraversal(root,a,&i);
    return a;  
}

二叉树的后序遍历

与上题相同

  int BTreeSize(struct TreeNode* root)
{
  if(root == NULL)
  {
    return 0;
  }
  int lcount = BTreeSize(root->left);
  int rcount = BTreeSize(root-> right);
  return lcount + rcount + 1;
  
}
void _postorderTraversal(struct TreeNode* root,int* a,int* i)
{
  if(root==NULL)
  {
    return;
  }
 
  _postorderTraversal(root->left,a,i);
  _postorderTraversal(root->right,a,i);
   a[(*i)++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
     *returnSize = BTreeSize(root);
    //malloc一个数组
    int* a = (int*)malloc(sizeof(int)*(*returnSize));
    //执行前序遍历
    //下标
    int i  = 0;
    _postorderTraversal(root,a,&i);
    return a;  
}

另一颗树的子树

在这里插入图片描述

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if(p==NULL&&q==NULL)
    {
        return true;
    }
    if(p==NULL||q==NULL)
    {
        return false;
    }
    if(p->val!=q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(root == NULL)
    {
        return false;
    }
    if(isSameTree(root,subRoot))
    {
        return true;
    }
    
    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

通过前序遍历的数组构建二叉树

#include <stdio.h>
#include <stdlib.h>
typedef struct BTNode
{
	char data;
	struct BTNode* left;
	struct BTNode* right;
}BTNode;

BTNode* BuyNode(char x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		perror("malloc failed!\n");
		return NULL;
	}
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}
BTNode* BinaryTreeCreate(char* a,int* pi)
{
    if(a[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
	//创建根节点
	BTNode* root = BuyNode(a[*pi]);
	(*pi)++;
	root->left = BinaryTreeCreate(a,pi);
	root->right = BinaryTreeCreate(a,pi);
	return root;
}
void InOrder(BTNode* root)
{
    if(root==NULL)
    {
        return;
    }
    InOrder(root->left);
    printf("%c ",root->data);
    InOrder(root->right);
}
int main() {
    int* a = (int*)malloc(sizeof(int)*100);
	scanf("%s",a);
	int pi = 0;
	BTNode* root = BinaryTreeCreate(a,&pi);
	InOrder(root);
}

判断二叉树是否是完全二叉树

在这里插入图片描述

//判断是否为完全二叉树
bool BTreeComplete(BT* root)
{
	//新建一个队列
	Que q;
	QueueInit(&q);
	//把root入队列
	QueuePush(&q, root);
	//队列不为空时继续遍历
	while (!QueueEmpty(&q))
	{
		//出队列
		BT* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			break;
		}
		//带入左右子树
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	while (!QueueEmpty(&q))
	{
		BT* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)   //遇到不为空证明不是完全二叉树
		{
			QueueDestory(&q);
			return false;
		}
	}
	QueueDestory(&q);
	return true;  //程序执行到这一步时，证明为完全二叉树
}

层序遍历

在这里插入图片描述

//二叉树的层序遍历
void LevelOrder(BT* root)
{
	//新建一个队列
	Que q;
	QueueInit(&q);
	//把root入队列
	QueuePush(&q, root);
	//队列不为空时继续遍历
	while (!QueueEmpty(&q))
	{
		//出队列
		BT* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		//带入左右子树
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	QueueDestory(&q);
}

k层节点数

// 二叉树第k层节点个数
int BTreeLevelKSize(BT* root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1; 
	}
	int left = BTreeLevelKSize(root->left, k - 1);
	int right = BTreeLevelKSize(root->right, k - 1);
	return left + right;
}

二叉树的销毁

递归展开图
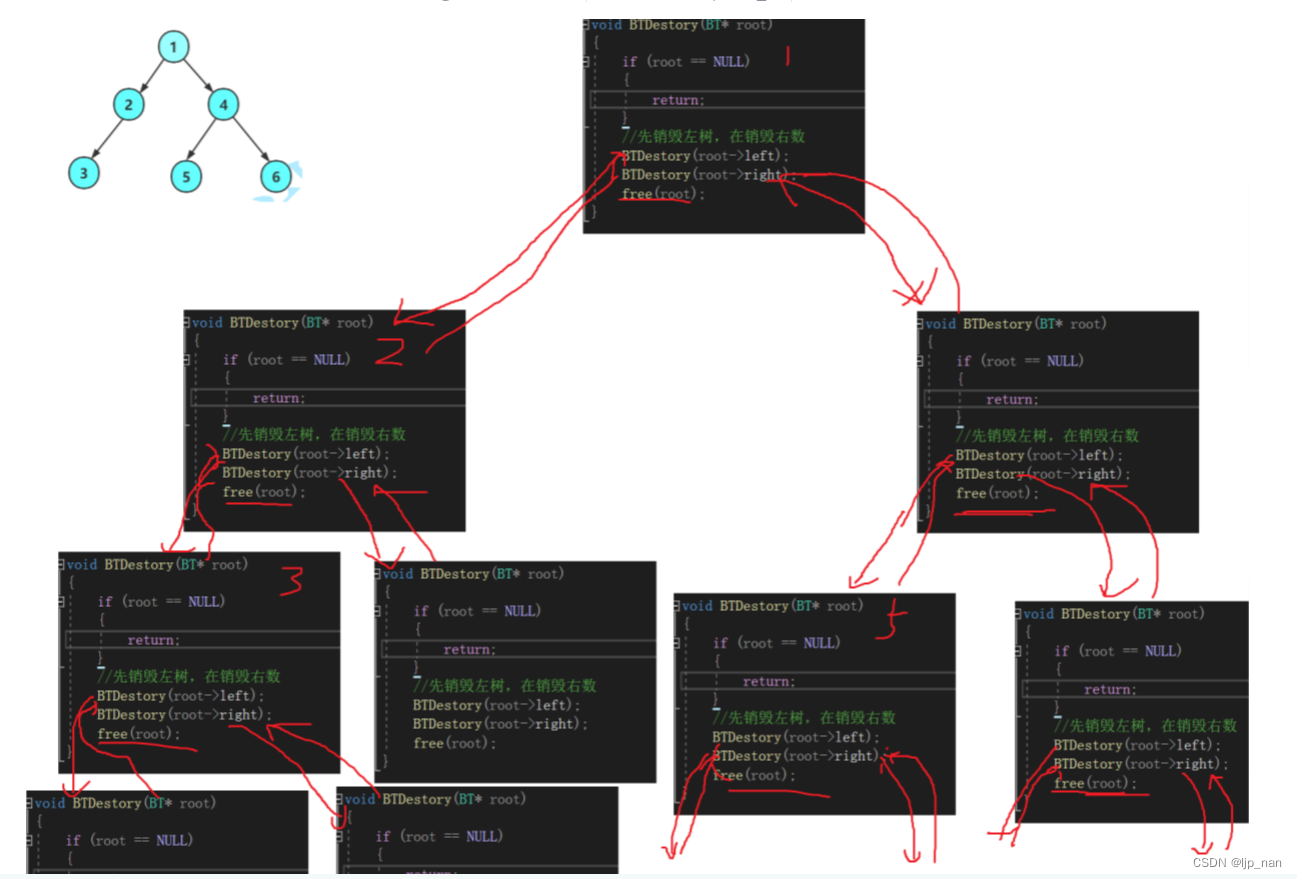
在这里插入图片描述

void BTDestory(BT* root)
{
	if (root == NULL)
	{
		return;
	}
	//先销毁左树，然后销毁右树，然后再销毁根
	BTDestory(root->left);
	BTDestory(root->right);
	free(root);
}

二叉树的整体

#include "Tree.h"
#include "Queue.h"
int BTreeLeafSize(BT* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
	
}
int BTreeSize(BT* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int lcount = BTreeSize(root->left);
	int rcount = BTreeSize(root->right);
	return lcount + rcount + 1;
}
int BTreeHeight(BT* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftheight = BTreeHeight(root->left);
	int rightheight = BTreeHeight(root->right);
	//return leftheight > rightheight ? leftheight + 1: rightheight + 1;0
	return 1 + (leftheight > rightheight ? leftheight : rightheight);
}

BT* BTreeFind(BT* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BT* left = BTreeFind(root->left, x);
	if (left)
	{
		return left;
	}
	BT* right = BTreeFind(root->right, x);
	if (right)
	{
		return right;
	}
	return NULL;
}

BT* BuyNode(BTDataType x)
{
	BT* node = (BT*)malloc(sizeof(BT));
	if (node == NULL)
	{
		perror("malloc failed!\n");
		return NULL;
	}
	node->data = x;
	node->left = NULL;
	node->right = NULL;
	return node;
}
BT* BTCreate()
{
	BT* node1 = BuyNode(1);
	BT* node2 = BuyNode(2);
	BT* node3 = BuyNode(3);
	BT* node4= BuyNode(4);
	BT* node5= BuyNode(5);
	BT* node6 = BuyNode(6);
	//BT* node7 = BuyNode(7);


	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

//二叉树的遍历
//先序遍历
void Prevorder(BT* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->data);
	Prevorder(root->left);
	Prevorder(root->right);
}
//中序遍历
void Inorder(BT* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	Inorder(root->left);
	printf("%d ", root->data);
	Inorder(root->right);
}
//后序遍历
void Postorder(BT* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	Postorder(root->left);
	Postorder(root->right);
	printf("%d ", root->data);
}

// 二叉树第k层节点个数
int BTreeLevelKSize(BT* root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1; 
	}
	int left = BTreeLevelKSize(root->left, k - 1);
	int right = BTreeLevelKSize(root->right, k - 1);
	return left + right;
}
//二叉树的层序遍历
void LevelOrder(BT* root)
{
	//新建一个队列
	Que q;
	QueueInit(&q);
	//把root入队列
	QueuePush(&q, root);
	//队列不为空时继续遍历
	while (!QueueEmpty(&q))
	{
		//出队列
		BT* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		//带入左右子树
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	QueueDestory(&q);
}

//判断是否为完全二叉树
bool BTreeComplete(BT* root)
{
	//新建一个队列
	Que q;
	QueueInit(&q);
	//把root入队列
	QueuePush(&q, root);
	//队列不为空时继续遍历
	while (!QueueEmpty(&q))
	{
		//出队列
		BT* front = QueueFront(&q);
		QueuePop(&q);
		if (front == NULL)
		{
			break;
		}
		//带入左右子树
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}
	while (!QueueEmpty(&q))
	{
		BT* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)   //遇到不为空证明不是完全二叉树
		{
			QueueDestory(&q);
			return false;
		}
	}
	QueueDestory(&q);
	return true;  //程序执行到这一步时，证明为完全二叉树
}
void BTDestory(BT* root)
{
	if (root == NULL)
	{
		return;
	}
	//先销毁左树，然后销毁右树，然后再销毁根
	BTDestory(root->left);
	BTDestory(root->right);
	free(root);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/708031.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Java基础---有了基本类型为什么还需要包装类

Java基础---有了基本类型为什么还需要包装类

目录 缘由 基本类型和包装类型的区别 如何理解自动拆装箱 哪些地方会自动拆装箱 自动拆装箱与缓存 缘由 Java中有8种基本数据类型&#xff0c;这些基本类型又都有对应的包装类 因为Java是一种面向对象语言&#xff0c;很多地方都需要使用对象而不是基本数据类型比如&…
阅读更多...
Domino Admin管理客户机中为每个管理域设置不同的图标

Domino Admin管理客户机中为每个管理域设置不同的图标

大家好&#xff0c;才是真的好。 一直在讲Domino管理中的单个网络 域&#xff0c;很少讲到多个Domino网络域的管理。其实&#xff0c;很多企业会有多个Domino网络域。因为以前多个部门或组织、企业等合并&#xff0c;或者隔离国内和国外的目录隔开等等&#xff0c;都会产生多个…
阅读更多...
从0-1手写一个RPC框架

从0-1手写一个RPC框架

前言 什么是RPC RPC&#xff08;Remote Procedure Call&#xff09;远程过程调用&#xff0c;简言之就是像调用本地方法一样调用远程服务。目前外界使用较多的有gRPC、Dubbo、Spring Cloud等。相信大家对RPC的概念都已经很熟悉了&#xff0c;这里不做过多介绍。 为啥要自己写…
阅读更多...
nvm 和 nrm安装使用

nvm 和 nrm安装使用

前端工具推荐&#xff1a;nvm&#xff08;Node 版本管理工具&#xff09; 和 nrm&#xff08;管理npm源&#xff09;&#xff1a; 一、nvm 1.1 nvm 是什么 1.2 安装 nvm 1.3 使用 nvm 二、nrm 2.1 nrm 是什么 2.2 安装 nrm 2.3 使用 nrm 一、nvm 如果直接将 node 安装到…
阅读更多...
20230701：成电的“七年之痒”，毕业啦

20230701：成电的“七年之痒”，毕业啦

毕业那些事儿 毕业随笔写在最后 毕业随笔 伴随着走完最后一道流程&#xff0c;成电7年&#xff0c;总算是毕业了。经济下行&#xff0c;行业寒冬&#xff0c;全被90后赶上了&#xff0c;庆幸学校的金字招牌让自己斩获了不少OFFER。荒废了半年的跑步和博客计划&#xff0c;接下…
阅读更多...
【测试开发】概念基础

【测试开发】概念基础

目录 一. 需求 1. 用户需求 2. 软件需求 3. 从测试人员的角度看需求 二. 测试用例 三. BUG 四. 开发模型 1. 软件的生命周期 2. 开发模型 2.1 瀑布模型 2.2 螺旋模型 2.3 增量&#xff0c;迭代模型 2.4 敏捷模型 SCRUM 五. 测试模型 1. V模型 2. W模型 (双V模…
阅读更多...
开源免费的多数据库工具Chat2DB

开源免费的多数据库工具Chat2DB

Chat2DB使用 当前使用的版本为1.0.11。 一.Chat2DB介绍 Chat2DB 是一款开源免费的多数据库客户端工具。 能够将自然语言转换为SQL&#xff0c;也可以将SQL转换为自然语言。 支持windows、mac本地安装&#xff0c;也支持服务器端部署&#xff0c;web网页访问。 支持多种数据库…
阅读更多...
Hexo基本建站

Hexo基本建站

目录 一、前言 二、Hexo安装、新建、启动 三、架构说明 四、写博客 五、打包 六、发布到GitHub 1.新建仓库 2.安装插件 3.修改配置文件&#xff1a;_config.yml 4.部署github 5.查看仓库 6.访问网站 一、前言 安装 Git安装 Node.js 二、Hexo安装、新建、启动 # 安装 h…
阅读更多...
智慧园区平台建设解决方案

智慧园区平台建设解决方案

智慧园区是指利用现代互联网物联网技术&#xff0c;对园区内的设施、设备和人员进行高效管理和智能化运营的一种模式。越来越多的城市开始致力于发展智慧园区&#xff0c;实现园区内的资源共享和高效利用。为了让智慧园区达到最佳的效果&#xff0c;我们需要从平台建设方面入手…
阅读更多...
Prettier - Code formatter配置(vscode)

Prettier - Code formatter配置(vscode)

1.安装Prettier 2.设置-->搜索format on save 并打勾 3.搜索default format 并选择Prettier - Code formatter 4.点击右上角打开setting.json 5.看最后一行是否存在如下配置,有就说明配置成功,没有重新前面步骤重新设置一下 6.根目录是否存在.prettierrc.json,没有创建一下 …
阅读更多...
vue3原理和源码分析 - watch 源代码

vue3原理和源码分析 - watch 源代码

https://github.com/vuejs/vue-next/blob/master/packages/runtime-core/src/apiWatch.ts 目录 Watch /packages/runtime-core/src/apiWatch.ts watch.dot https://github.com/vuejs/vue-next/blob/master/packages/runtime-core/src/apiWatch.ts Watch /packages/runtime…
阅读更多...
6.3 B树,B+树

6.3 B树,B+树

多路平衡查找树 1.定义 B树的阶&#xff1a;B树中所有结点的孩子个数的最大值&#xff0c;表示成m m阶B树&#xff1a;空树或者满足如下特性的m叉树 特性&#xff1a; 1.树中每个结点最多子树 m 关键字m-1 2.根节点不是终端结点&#xff0c;至少有两棵子树 3.根结点除外&…
阅读更多...
基于Elasticsearch + Fluentd + Kibana（EFK）搭建日志收集管理系统

基于Elasticsearch + Fluentd + Kibana（EFK）搭建日志收集管理系统

目录 1、EFK简介 2、EFK框架 2.1、Fluentd系统架构 2.2、Elasticsearch系统架构 2.3、Kibana系统架构 3、Elasticsearch接口 4、EFK在虚拟机中安装步骤 4.1、安装elasticsearch 4.2、安装kibana 4.3、安装fluentd 4.4、进入kibana创建索引 5、Fluentd配置介绍 Elas…
阅读更多...
2023年最受欢迎和最佳WordPress主题(专家精选)

2023年最受欢迎和最佳WordPress主题(专家精选)

您在找2023年最佳WordPress主题吗&#xff1f; 免费和高级WordPress主题有数以千计&#xff0c;初学者很难为他们的网站选择合适的WordPress主题。 在本文中&#xff0c;我们将分享我们专家精选的2023年所有最受欢迎和最佳的WordPress主题。 本文网址: 2023年最受欢迎和最佳…
阅读更多...
Nautilus Chain 推出全新 Layer3 DID 公民身份，限量 10 万枚免费发放

Nautilus Chain 推出全新 Layer3 DID 公民身份，限量 10 万枚免费发放

Nautilus Chain 是目前行业内首个模块化的 Layer3 机构链&#xff0c;该链此前基本完成了测试网的早期测试&#xff0c;并有望在近期上线主网。Nautilus Chain 近阶段市场活动频频&#xff0c;除了此前举办全球行活动推广 Layer3 概念外&#xff0c;其也在同期联合 Stanford Bl…
阅读更多...
wps文档忘记保存关闭了怎么恢复

wps文档忘记保存关闭了怎么恢复

1、点击WPS左上角小箭头&#xff0c;点击下拉菜单中的工具选项&#xff0c;然后点击里面的备份中心。 2、在WPS的右侧会看到备份中心的小窗口&#xff0c;里面有自动备份的文件&#xff0c;还可以点击一键恢复即可复原之前的文件内容。 可以对之前时间段的文件打开。
阅读更多...
什么是内存溢出，什么是内存泄漏？

什么是内存溢出，什么是内存泄漏？

文章目录 一、什么是内存溢出&#xff1f;二、什么是内存泄漏&#xff1f;三、如何避免&#xff1f; 提示&#xff1a;以下是本篇文章正文内容&#xff0c;下面案例可供参考 一、什么是内存溢出&#xff1f; 假设我们 JVM 中可用的内存空间只剩下 3M&#xff0c;但是我们要创…
阅读更多...
Maven manual

Maven manual

Download maven Download 设置 system env… E:\apache-maven-3.9.3\bin查看版本信息 mvn -v Apache Maven 3.9.3 (21122926829f1ead511c958d89bd2f672198ae9f) Maven home: E:\apache-maven-3.9.3与Eclipse integrate Referrence&#xff0c;通常Eclipse原本就已经集成&am…
阅读更多...
[STC32F12K54入门第三步]USART1+Modbus RTU从机

[STC32F12K54入门第三步]USART1+Modbus RTU从机

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 一、Modbus RTU是什么？二、Modbus RTU程序展示1.串口配置2.Timer定时器配置3.配置CRC16校验位和Modbus RTU发送函数4.主函数5.效果展示总结提示：以下是本篇文章正文内容，下面案例可供参考 一、…
阅读更多...
WebMvcConfigurationSupport 和 WebMvcConfigurer 区别和同时使用产生的问题-解决

WebMvcConfigurationSupport 和 WebMvcConfigurer 区别和同时使用产生的问题-解决

在Spring Boot 1.5版本都是靠重写WebMvcConfigurerAdapter的方法来添加自定义拦截器&#xff0c;消息转换器等。SpringBoot 2.0 后&#xff0c;该类被标记为Deprecated&#xff08;弃用&#xff09;。 在Spring Boot 2.0后用自己的的配置类继承WebMvcConfigurerAdapter时&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023