信道编码【编码、纠错检错】

差错控制的基本概念--数字信号在传输过程中，由于信道传输特性不理想及加性噪声的影响，不可避免地会发生错误。

可通过以下三方面的措施来减小误码率：1）提高信道容量；2）降低编码效率；3）增加码长。差错控制不仅广泛应用于各种通信系统中，而且在计算机、磁记录于存储设备中也得到大量的应用。

扰离散信道的编码定理：

扰离散信道编码定理（Channel Coding Theorem）是信息论中的基本定理之一，其表述了在扰动信道条件下，通过编码可以实现错误概率任意小的通信的可能性。

该定理由香农在其经典的《通信的数学理论》中提出。定理的核心思想是，在给定的信道容量下，存在一种编码方案，通过添加冗余信息，使得信息可以以任意小的错误概率进行传输。

具体而言，假设信道的容量为C，那么对于任意小的正数ε，存在一种编码方式，使得在编码后的数据长度大于C时，错误概率小于ε。

扰离散信道编码定理的意义在于，通过适当的编码和解码算法，我们可以在有限的信道容量下实现可靠的信息传输。这为通信系统设计和研究提供了重要的理论基础。

需要注意的是，扰离散信道编码定理是基于理想条件的理论结果，并假设信道状态信息是已知的。在实际应用中，由于通信环境的复杂性和信道特性的不确定性，实际的编码和解码算法通常需要结合信道估计、纠错编码、调制等技术，以尽可能地接近理论的极限。

最小码距和检错：

在信息码序列中加监督码元，监督码和信息码之间存在一种逻辑关系。因此，收端可以利用这种逻辑关系发现或纠正存在的错码。

一般来说，监督码越多，检、纠错能力越强。用降低传输速率换取传输可靠性的提高。

不同的编码方法，有不同的检错或纠错能力。

目标：监督码元要少，检、纠能力要强。

分组码：将信息码分组，为每组信息码后附加若干监督码元形成的码集合。

特点：分组码中的监督码元仅监督本码组中的信息码元。

符号（n,k），k是码组中信息码元的数目，n为码组长度，r=n-k，为码组中监督码元的数目。

结构：

码组重量：码组中“1”的数目

码组d：两个码组对应位上不同的码元个数，称为汉明距离。

最小码距d0：码集合中任意两两码组间距离的最小值。

码距与码集合检、纠错能力的关系：

检测e个错吗，要求最小码距d0>=e+1

纠正t个错吗，要求最小码距d0>=2t+1

纠正t个错码、同时检测e个错码，要求最小码距d0>=e+t+1

可通过监督矩阵来判断是否出错，通过生成矩阵来编码。

【监督矩阵、生成矩阵的知识较多，且较容易查找，这里不介绍】

常用检错码：

常用的检错码包括奇偶校验码、循环冗余校验码、海明码、卷积码等等。

1. 奇偶校验码：是一种简单的检错码，通过在数据中增加一个奇偶位来实现错误检测。奇偶校验码适用于单比特错误的检测，但无法纠正错误。

2. 循环冗余校验码（CRC）：是一种广泛使用的检错码，常用于数据通信和存储系统中。CRC通过生成多项式来计算校验码，并将校验码附加到原始数据中。接收端根据接收到的数据和校验码重新计算校验码，如果两者不一致，则表明数据存在错误。CRC能够有效检测多比特错误。

3. 海明码：是一种能够检测和纠正单比特错误的编码方案。海明码通过在原始数据中增加冗余比特，使得接收端可以检测到并纠正单比特的错误。海明码的纠错能力取决于冗余比特的数量。

4. 卷积码：是一种线性移位寄存器编码的纠错码。卷积码为每个输入比特添加一个或多个冗余比特，以实现错误检测和纠正。卷积码的性能优秀，广泛应用于无线通信系统。

这些是常见的检错码，每种检错码在不同的应用场景下有着不同的优缺点。在实际应用中，根据具体需求可以选择适合的检错码来保证数据的可靠传输和存储。

卷积码：

卷积码是伊莱亚斯于1955年提出的一种非分组码。

卷积码每个码组中的监督码不但与本码组的信息码有关，还与前边(N-1)个码组中的信息码有关。

设一个码组的码长为n，n×N称为约束长度，N称为约束度。卷积码的纠错能力也随N的增大而增强，卷积码是具有记忆性。一般用(n，k，N) 表示卷积码。

卷积码的k和n值可以为比较小的值，编、译码延时小。在相同的传信率和设备复杂度的条件下，卷积码的性能一般优于线性分组码。

例：（3，1，2）卷积码

卷积码的表示方法有解析表示、图解表示。

i）解析表示---当第1个信息码元m1输入时，输出为，y11=m1，y12=m1，y13=m1；

当第2个信息码元m2输入时，输出为y21=m2，y22=m2，y23=m1+m2；......

上面各符号的第1为下表是码元所在的码组编号，第2位下标表示码元在码组中的位置。

把上面的表达式写成矩阵的形式：

卷积码的生成矩阵和监督矩阵式有头无尾的半无穷矩阵，不便于研究，但也有规律可循。

ii）图解表示

树状图-------

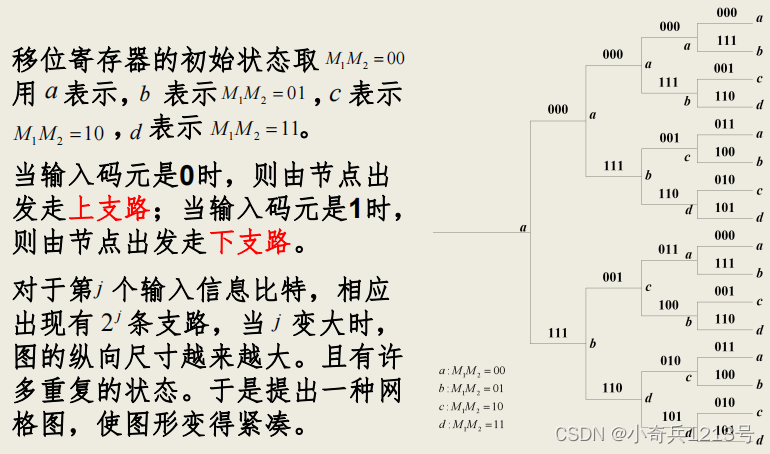
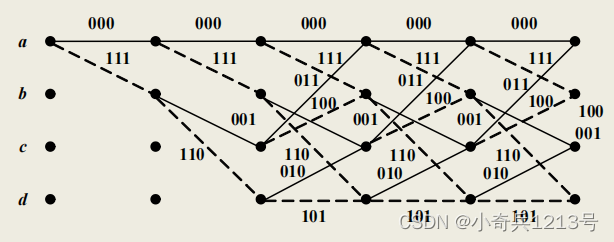
网格图-------把码树中具有相同状态的节点合并在一起；码树中的上支路（输入0）用实线表示，下支路（输入1）用虚线表示；支路上标注的码元为输出比特。

网格图中的状态，通常有2^(n-1)种状态。从第个节点开始，图形开始重复，且完全相同。

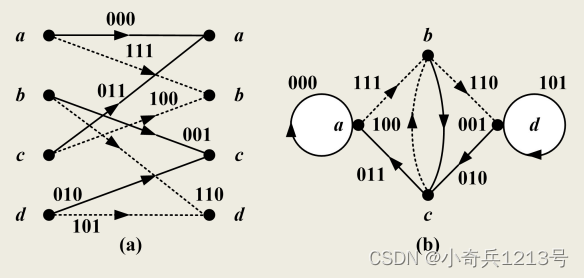
状态图---------取出达到稳定状态后两个节点间的一段网格图，即得到状态转移图和最简的状态转移图，称之为卷积码状态图。

两种译码方法：

建立在代数译码基础上的门限译码，又称为大数逻辑译码。

最大似然译码，又称为概率译码。

维特比译码属于最大似然译码。

维特比译码算法简称VB算法，是1967年由Viterbi提出。

基本思路：

把已接收序列与所有可能的发送序列做比较，选择其中码距最小的一个序列作为发送序列。如果发送L组信息比特，发送的序列组合有2^kl个，需要存储所有这些序列并进行比较，以找到码距最小的那个序列。当传信率和信息组数较大时，译码器将变得非常复杂。

VB算法进行了简化，成为了一种实用化的概率算法。它并不是在网格图上一次比较所有可能的条路径（序列），是接收一段，计算和比较一段，选择一段有最大似然可能的码段，从而达到整个码序列是一个有最大似然值的序列。

如下图的卷积码编码器

VB算法进行了简化，成为了一种实用化的概率算法。它并不是在网格图上一次比较所有可能的条路径（序列），而是接收一段，计算和比较一段，选择一段有最大似然可能的码段，从而达到整个码序列是一个有最大似然值的序列。对于(n，k，N) 卷积码，首先考察接收序列的前nN位。比较网格图中可能的路径和接收序列之间的汉明距离，保留到达每个状态的两条路径中汉明距离小的一条路径，称为幸存路径。

继续考察接收序列中的后继n位，在增加的一级可能的路径中，通过比较汉明距离保留幸存路径。如此继续进行。

循环码是线性分组码中一种重要的编码。它是在严密的代数理论基础上建立起来的。其编码和解码不太复杂，但检(纠)错的能力较强。循环码除了具有线性码的一般性质外，还具有循环性。

（其中有码的多项式、码多项式的模运算、余式等，根据生成矩阵和g(x)可以计算得到传输的循环码）