【深度学习】日常笔记8

过拟合是指模型在训练集上表现良好，但在验证集和测试集上表现不佳的现象。这是因为模型在训练过程中过度学习了训练数据中的噪声和细节，而忽略了更一般的特征和规律，导致模型泛化能力不足。

具体来说，当模型在训练集上进行训练时，它会尝试通过学习训练数据中的特征来预测新的数据点。然而，如果模型过于复杂或过于依赖于训练数据中的噪声和细节，它可能会过度拟合这些特征，从而导致在验证集和测试集上的表现不佳。

例如，假设我们有一个简单的线性回归模型，它试图通过学习训练数据中的一些特征来预测新数据点的值。如果我们在训练集中添加了一些噪声或异常值，那么模型可能会过度拟合这些噪声和异常值，从而导致在验证集和测试集上的表现不佳。

因此，为了避免过拟合，我们需要采取一些措施来提高模型的泛化能力，例如增加正则化项、使用dropout等技术、减少模型的复杂度等

torch.optim.SGD(params, lr=lr).step()中的step()方法不需要参数，它是用来执行优化器的一步更新操作的。

在使用梯度下降算法进行优化时，通常需要执行以下几个步骤：

1. 计算损失函数关于模型参数的梯度。

2. 使用优化器更新模型参数，以减小损失函数的值。

step()方法就是负责执行第2步的操作。它根据计算得到的梯度信息和设置的学习率（lr）对模型的参数params进行更新。具体而言，它会根据优化器的算法（如随机梯度下降）来更新参数，使其朝着较小的损失方向移动。

可以在迭代训练过程中多次调用step()方法来进行多次参数更新。一般情况下，在每个训练批次或每个训练样本上都会调用一次step()方法。

需要注意的是，step()方法必须在反向传播（即计算梯度）之后调用，以确保最新的梯度信息被正确地应用于参数更新。

p140练习

5. 描述为什么涉及多个超参数更具挑战性。

答：

涉及多个超参数的模型训练更具挑战性，原因如下：

1. 复杂性增加：当模型具有多个超参数时，需要调整的参数数量会大大增加。这意味着需要更多的数据来确定每个超参数的最佳值，从而增加了模型训练的复杂性。

2. 难以解释：多个超参数可能导致模型的行为变得难以解释。在这种情况下，很难确定哪个超参数对模型性能的影响最大。这可能会导致模型在实际应用中的不确定性和不稳定性。

3. 过拟合和欠拟合：由于存在多个超参数，模型可能更容易出现过拟合或欠拟合的问题。例如，如果某个超参数设置得过高，模型可能会过度拟合训练数据，导致在新数据上的泛化能力较差；相反，如果某个超参数设置得过低，模型可能会欠拟合训练数据，导致性能不佳。

4. 计算资源需求：调整多个超参数通常需要更多的计算资源。例如，在深度学习中，需要为每个超参数单独训练一个子模型，并使用交叉验证等技术来选择最佳超参数组合。这会导致计算成本显著增加。

5. 时间需求：为了找到最佳的超参数组合，可能需要进行多次迭代和实验。这可能需要大量的时间和精力，特别是在处理大量超参数的情况下。

总之，涉及多个超参数的模型训练更具挑战性，因为它涉及到更多的复杂性、难以解释的行为、过拟合和欠拟合的风险、计算资源需求以及时间需求。为了解决这些问题，研究人员和工程师需要采用更有效的方法来调整超参数，如网格搜索、随机搜索、贝叶斯优化等。

6. 如果想要构建多个超参数的搜索⽅法，请想出⼀个聪明的策略。

答：

要构建一个聪明的策略来搜索多个超参数，可以考虑以下步骤：

1. 确定目标：首先需要明确模型的目标和性能指标。这将有助于确定需要调整的超参数类型和数量。

2. 选择搜索空间：根据目标和性能指标，选择合适的超参数空间。例如，对于神经网络模型，可以选择学习率、批量大小、隐藏层大小等作为超参数。

3. 网格搜索：使用网格搜索方法来搜索超参数空间。网格搜索是一种穷举搜索方法，它会遍历所有可能的超参数组合，并计算每个组合的性能指标。这种方法可以找到最优的超参数组合，但计算成本较高。

4. 随机搜索：与网格搜索相比，随机搜索是一种更高效的搜索方法。它从超参数空间中随机选择一些超参数组合，并计算它们的性能指标。然后，根据性能指标选择最佳的超参数组合。这种方法比网格搜索更快，但可能无法找到全局最优解。

5. 贝叶斯优化：贝叶斯优化是一种基于概率模型的优化方法。它通过利用先验知识和后验信息来更新超参数的估计值，以最小化预测误差。这种方法可以在较短的时间内找到较好的超参数组合，并且可以处理高维空间中的复杂问题。

6. 交叉验证：在搜索过程中，可以使用交叉验证来评估不同超参数组合的性能。交叉验证可以将数据集分成训练集和测试集，并使用训练集来训练模型，然后使用测试集来评估模型的性能。这可以帮助我们更好地了解不同超参数组合对模型性能的影响。

总之，要构建一个聪明的策略来搜索多个超参数，需要选择合适的超参数空间、使用网格搜索、随机搜索或贝叶斯优化等方法来搜索最优的超参数组合，并使用交叉验证来评估不同超参数组合的性能。

nn.Sequential是PyTorch中的一个类，用于将多个神经网络层按顺序连接起来。它可以方便地构建深度神经网络模型。

而nn.Linear是PyTorch中的一个类，用于定义线性层。线性层是一种全连接层，可以将输入的向量映射到输出的向量。

交叉熵损失的公式中的y^通常指的是softmax函数给出的预测概率。

练习p141

1. 尝试添加不同数量的隐藏层（也可以修改学习率），怎么样设置效果最好？

代码：

import torch
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

答：要确定最佳的隐藏层数量和学习率，可以使用交叉验证(cross-validation)方法。

K折交叉验证是一种常用的模型评估方法，它将数据集分成K个子集，每次使用其中的K-1个子集作为训练集，剩下的一个子集作为测试集。然后重复这个过程K次，最后计算这K次实验的平均结果，以得到模型的最终评估结果。

以下是使用PyTorch中的K折交叉验证来评估不同隐藏层数量和学习率的效果，在代码中，KFold(n_splits=5)表示将数据集分成5份进行交叉验证。其中，n_splits参数指定了要将数据集分成多少份。在这个例子中，我们将数据集分成5份进行交叉验证，因此使用了KFold(n_splits=5)来创建一个K折交叉验证对象。

要确定最佳的隐藏层数量和学习率，可以使用交叉验证(cross-validation)方法。以下是使用PyTorch中的K折交叉验证来评估不同隐藏层数量和学习率的效果：

import torch
from torch import nn
from d2l import torch as d2l
from sklearn.model_selection import KFold
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)
batch_size, num_epochs = 256, 10
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD(net.parameters(), lr=0.1)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
kf = KFold(n_splits=5) # 将数据集分成5份进行交叉验证
best_acc = 0 # 初始化最佳准确率为0
for train_index, val_index in kf.split(train_iter): # 对训练集和验证集进行划分
X_train, X_val = [x[train_index] for x in train_iter], [x[val_index] for x in train_iter] # 分别获取训练集和验证集的数据
y_train, y_val = [y[train_index] for y in test_iter], [y[val_index] for y in test_iter] # 分别获取训练集和验证集的标签
X_train, y_train = torch.tensor(X_train), torch.tensor(y_train) # 将数据转换为PyTorch张量格式
X_val, y_val = torch.tensor(X_val), torch.tensor(y_val) # 将数据转换为PyTorch张量格式
net.train() # 在验证集上进行训练时需要将模型设置为训练模式
trainer.zero_grad() # 将梯度清零
y_pred = net(X_val) # 在验证集上进行预测
loss = loss(y_pred, y_val).mean() # 计算损失函数值
loss.backward() # 反向传播计算梯度
trainer.step() # 更新模型参数
val_acc = (y_pred.argmax(dim=1) == y_val).float().mean() # 在验证集上计算准确率
if val_acc > best_acc: # 如果当前验证集上的准确率比之前的最佳准确率高，则更新最佳准确率和模型参数
best_acc = val_acc
best_net = net.state_dict() # 保存当前模型参数到字典中
d2l.save('best_net.pt', best_net) # 将模型参数保存到文件中以备后续使用

3. 尝试不同的⽅案来初始化权重，什么⽅法效果最好？

答：在神经网络中，权重初始化是一个非常重要的步骤，因为它会影响到模型的训练效果和泛化能力。以下是一些常用的权重初始化方法：

1. 随机初始化(Random Initialization):将权重随机初始化为一个均匀分布或正态分布的随机数。这种方法简单易行，但可能会导致梯度消失或梯度爆炸的问题。

2. Xavier/Glorot 初始化(Xavier/Glorot Initialization):根据输入和输出神经元的数量来确定权重的初始值。具体来说，对于输入层，将权重初始化为其中 $n$ 是输入神经元的数量；对于隐藏层，将权重初始化为 $其中 n 是隐藏层神经元的数量。这种方法可以有效地缓解梯度消失和梯度爆炸问题，并且适用于各种类型的神经网络。

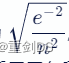3. He 初始化(He Initialization):根据输入和输出神经元的数量来确定权重的初始值。具体来说，对于输入层，将权重初始化为其中 n 是输入神经元的数量；对于隐藏层，将权重初始化为 ,其中 n 是隐藏层神经元的数量。这种方法可以有效地缓解梯度消失和梯度爆炸问题，并且适用于各种类型的神经网络。