存货
import tushare as ts
# 导包
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import find_peaks
from scipy.stats import norm
import datetime
import pandas as pd
import seaborn as sns # pip install seaborn
import matplotlib.patches as mpatches
#from empyrical import sharpe_ratio,omega_ratio,alpha_beta,stats # pip install empyrical
import warnings
warnings.filterwarnings('ignore')
ts.set_token('066decd1fadb71f9a675e3baa40bb0cb56e58815cf10682709b96315')
api = ts.pro_api()
#获取宁德时代股票数据
NDSD = api.query('daily',ts_code='300750.SZ',start_date='20190901',end_date='20220630')
#获取比亚迪股票数据
BYD = api.query('daily',ts_code='002594.SZ',start_date='20190901',end_date='20220630')
#获取隆基绿能股票数据
LJLN = api.query('daily',ts_code='601012.SH',start_date='20190901',end_date='20220630')
LJLN
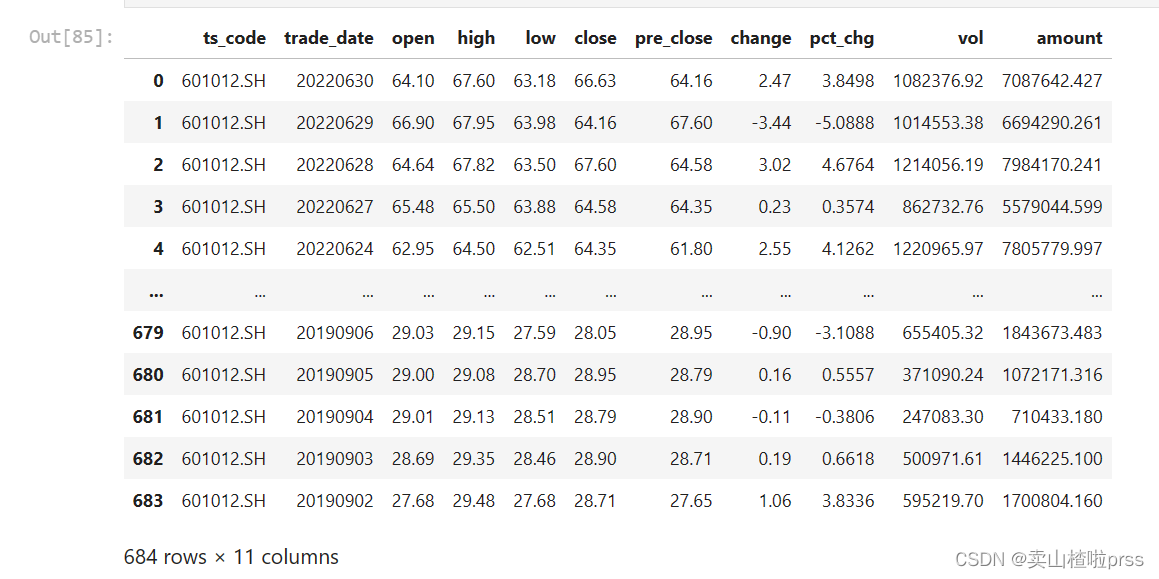
#存放3家公司的收盘价
closeDf = pd.DataFrame()
#合并3家公司的收盘价
closeDf = pd.concat([closeDf,NDSD['trade_date'],NDSD['close'],BYD['close'],LJLN['close']],axis=1)
#重命名列名为公司名称
closeDf.columns=['日期','宁德时代','比亚迪','隆基绿能']
#将日期设置为行索引
closeDf['日期'] = pd.to_datetime(closeDf['日期'])
closeDf.set_index('日期',inplace=True)
closeDf = closeDf.sort_index(ascending=True)
closeDf
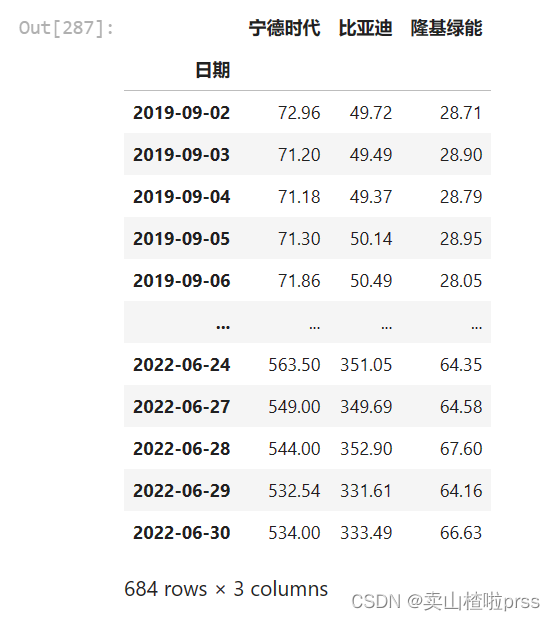
# 配对策略
# Analysis object:BYD&GM
# Comparison of closing price line chart
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.style.use('ggplot')
ax1 = closeDf.plot(y='宁德时代',label='宁德时代',figsize=(16,8))
closeDf.plot(ax=ax1,y='比亚迪',label='比亚迪')
closeDf.plot(ax=ax1,y='隆基绿能',label='隆基绿能')
plt.title('Closing price comparison')
plt.xlabel('Date')
plt.ylabel('Close')
plt.grid(True)
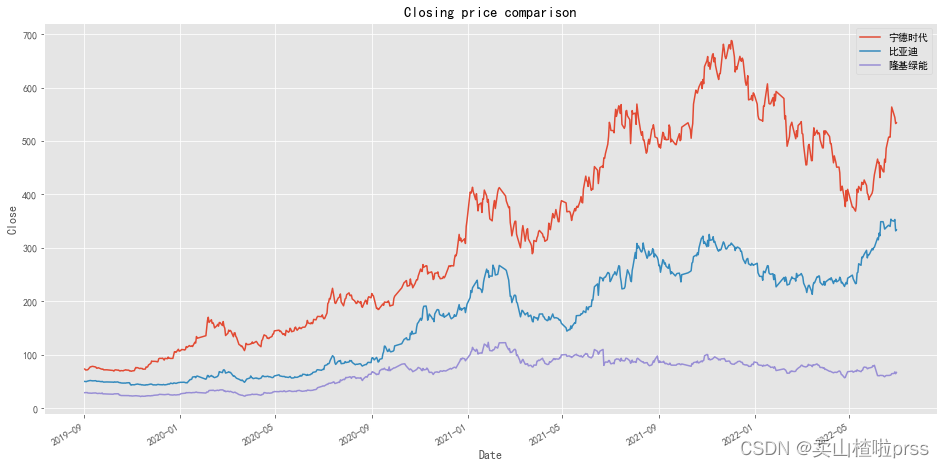
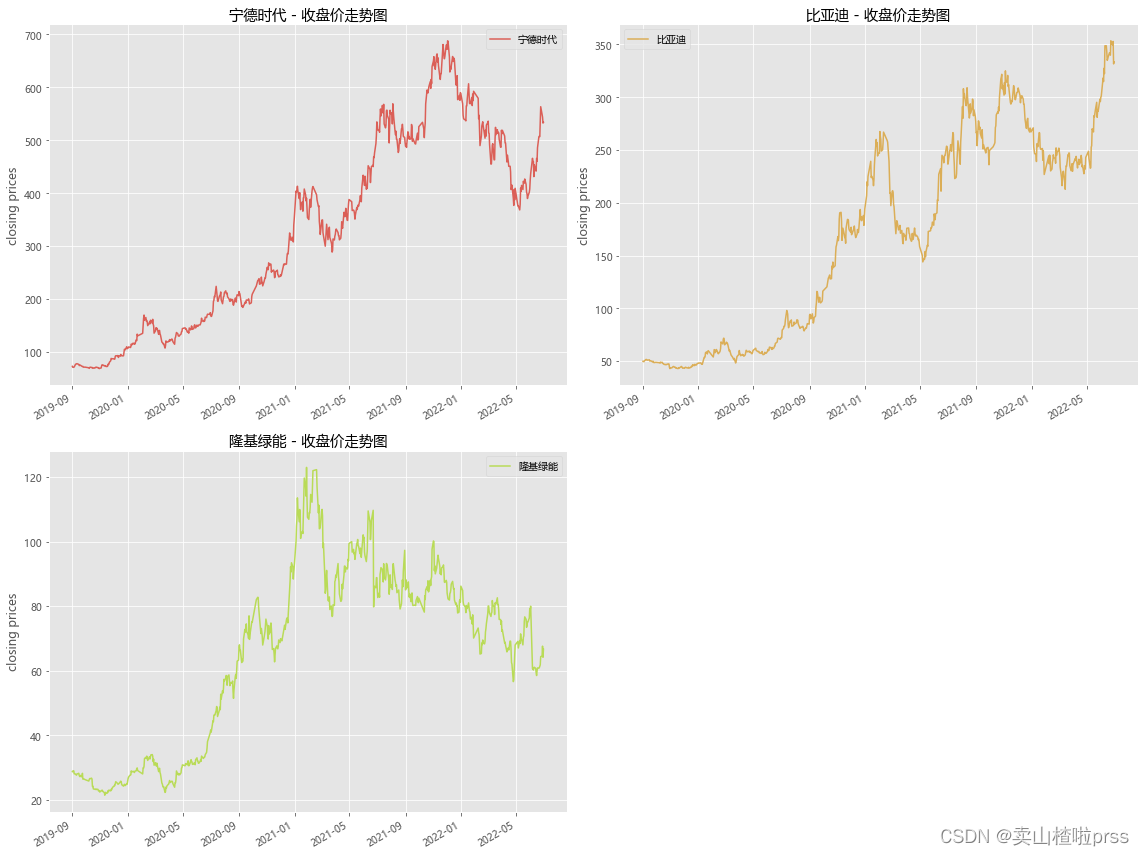
# 收盘价走势
plt.style.use('ggplot') # 样式
color_palette=sns.color_palette("hls",10) # 颜色
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
fig = plt.figure(figsize = (16,12))
tickers = ['宁德时代','比亚迪','隆基绿能']
for i,j in enumerate(tickers):
plt.subplot(2,2,i+1)
closeDf[j].plot(kind='line', style=['-'],color=color_palette[i],label=j)
plt.xlabel('')
plt.ylabel('closing prices')
plt.title('{} - 收盘价走势图'.format(j))
plt.legend()
plt.tight_layout()
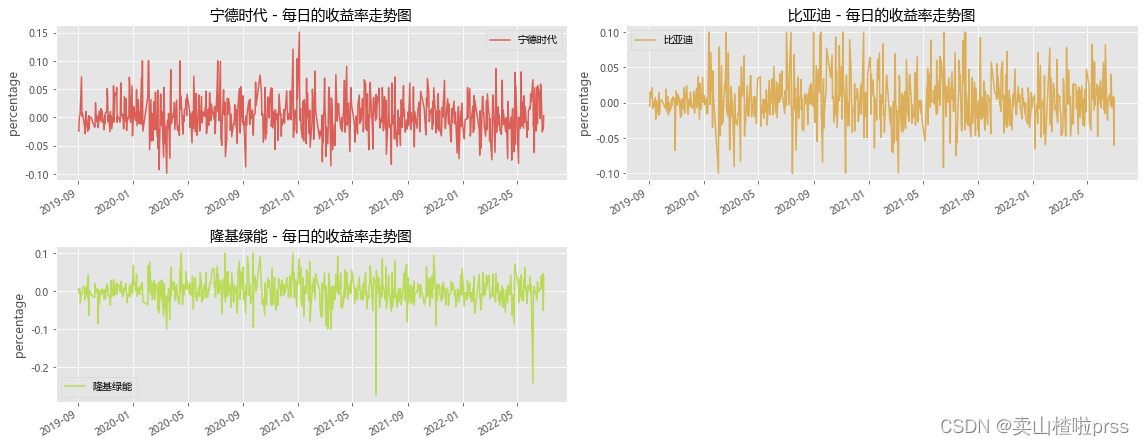
# 每日的收益率走势
plt.style.use('ggplot')
color_palette=sns.color_palette("hls",10)
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
fig = plt.figure(figsize = (16,15))
tickers = ['宁德时代','比亚迪','隆基绿能']
for i,j in enumerate(tickers):
plt.subplot(5,2,i+1)
closeDf[j].pct_change().plot(kind='line', style=['-'],color=color_palette[i],label=j)
plt.xlabel('')
plt.ylabel('percentage')
plt.title('{} - 每日的收益率走势图'.format(j))
plt.legend()
plt.tight_layout()
# 日平均收益
tickers = ['宁德时代','比亚迪','隆基绿能']
for i in tickers:
r_daily_mean = ((1+closeDf[i].pct_change()).prod())**(1/closeDf[i].shape[0])-1
#print("%s - Average daily return:%f"%(i,r_daily_mean))
print("%s - 日平均收益:%s"%(i,str(round(r_daily_mean*100,2))+"%"))

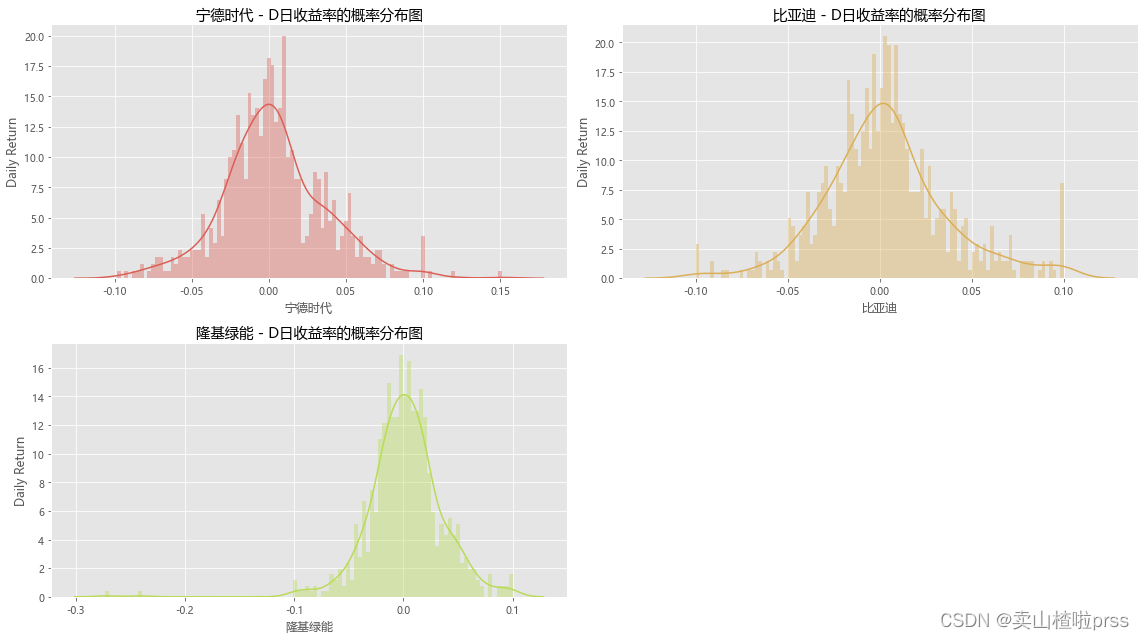
# 日收益率的概率分布图
# 查看分布情况
plt.style.use('ggplot')
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
fig = plt.figure(figsize = (16,9))
for i,j in enumerate(tickers):
plt.subplot(2,2,i+1)
sns.distplot(closeDf[j].pct_change(), bins=100, color=color_palette[i])
plt.ylabel('Daily Return')
plt.title('{} - D日收益率的概率分布图'.format(j))
plt.tight_layout();
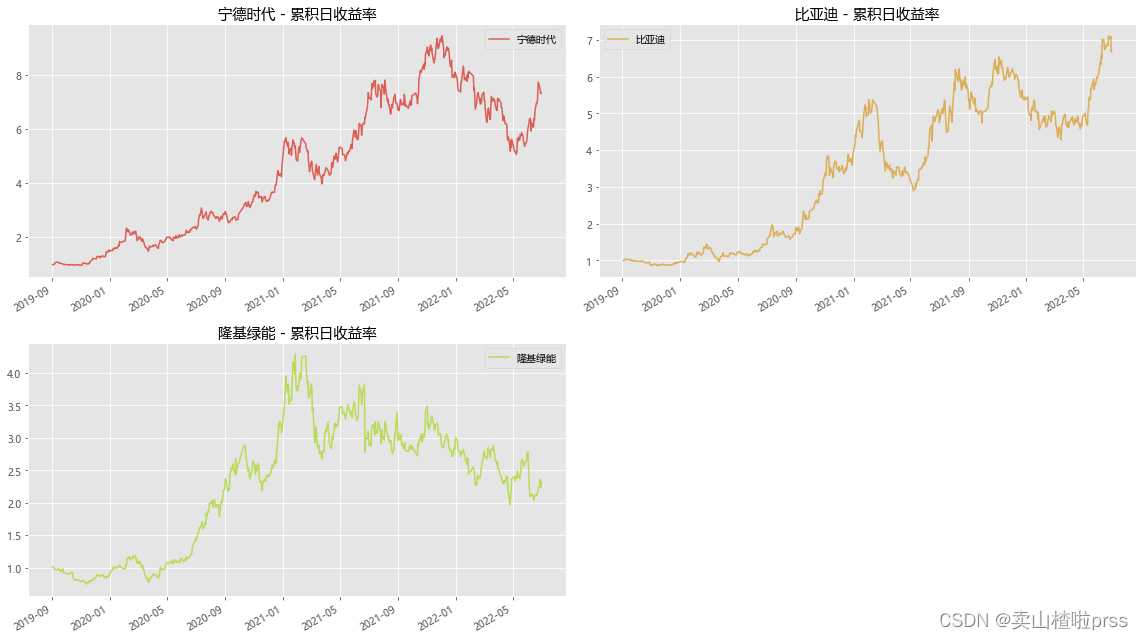
# 累积日收益率
# 累积日收益率有助于定期确定投资价值。可以使用每日百分比变化的数值来计算累积日收益率,只需将其加上1并计算累积的乘积。
# 累积日收益率是相对于投资计算的。如果累积日收益率超过1,就是在盈利,否则就是亏损。
plt.style.use('ggplot')
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
fig = plt.figure(figsize = (16,9))
for i,j in enumerate(tickers):
plt.subplot(2,2,i+1)
cc = (1+closeDf[j].pct_change()).cumprod()
cc.plot(kind='line', style=['-'],color=color_palette[i],label=j)
plt.xlabel('')
plt.title('{} - 累积日收益率'.format(j))
plt.legend()
plt.tight_layout()
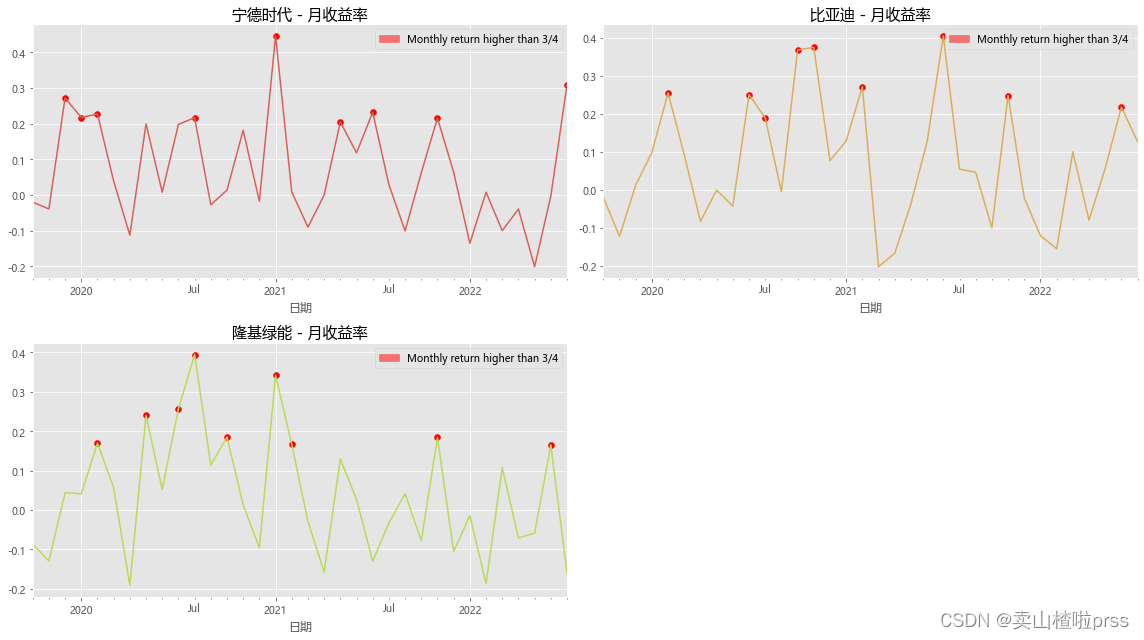
# 月收益率
# 对月收益率进行可视化分析,标注收益率高于四分之三分位数的点。
# 月收益率围绕均线上下波动
fig = plt.figure(figsize = (16,9))
for i,j in enumerate(tickers):
plt.subplot(2,2,i+1)
daily_ret = closeDf[j].pct_change()
mnthly_ret = daily_ret.resample('M').apply(lambda x : ((1+x).prod()-1))
mnthly_ret.plot(color=color_palette[i]) # Monthly return
start_date=mnthly_ret.index[0]
end_date=mnthly_ret.index[-1]
plt.xticks(pd.date_range(start_date,end_date,freq='Y'),[str(y) for y in range(start_date.year+1,end_date.year+1)])
# Show points with monthly yield greater than 3/4 quantile
dates=mnthly_ret[mnthly_ret>mnthly_ret.quantile(0.75)].index
for i in range(0,len(dates)):
plt.scatter(dates[i], mnthly_ret[dates[i]],color='r')
labs = mpatches.Patch(color='red',alpha=.5, label="Monthly return higher than 3/4")
plt.title('%s - 月收益率'%j,size=15)
plt.legend(handles=[labs])
plt.tight_layout()
# 月平均收益
plt.style.use('ggplot')
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
fig = plt.figure(figsize = (15,9))
for i,j in enumerate(tickers):
plt.subplot(2,2,i+1)
daily_ret = closeDf[j].pct_change()
mnthly_ret = daily_ret.resample('M').apply(lambda x : ((1+x).prod()-1))
mrets=(mnthly_ret.groupby(mnthly_ret.index.month).mean()*100).round(2)
attr=[str(i)+'m' for i in range(1,13)]
v=list(mrets)
plt.bar(attr, v,color=color_palette[i],label=j)
for a, b in enumerate(v):
plt.text(a, b+0.08,b,ha='center',va='bottom')
plt.title('{}- 月平均收益 '.format(j))
plt.legend()
plt.tight_layout()
# 图中显示某些月份具有正的收益率均值,而某些月份具有负的收益率均值,
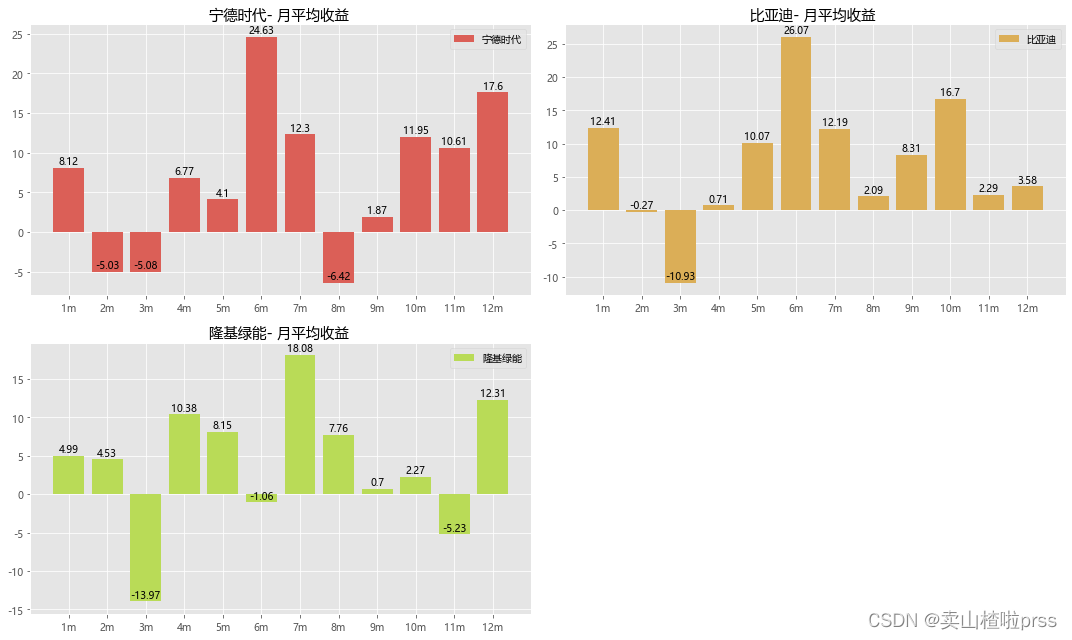
Three year compound annual growth rate (CAGR)
复合年增长率(Compound Annual Growth Rate,CAGR)是一项投资在特定时期内的年度增长率 CAGR=(现有价值/基础价值)^(1/年数) - 1 或 (end/start)^(1/# years)-1
它是一段时间内的恒定回报率。换言之,该比率告诉你在投资期结束时,你真正获得的收益。它的目的是描述一个投资回报率转变成一个较稳定的投资回报所得到的预想值
# 复合年增长率(CAGR)
for i in tickers:
days = (closeDf[i].index[0] - closeDf[i].index[-1]).days
CAGR_3 = (closeDf[i][-1]/ closeDf[i][0])** (365.0/days) - 1
print("%s (CAGR):%s"%(i,str(round(CAGR_3*100,2))+"%")

# 年化收益率
# 年化收益率,是判断一只股票是否具备投资价值的重要标准!
# 年化收益率,即每年每股分红除以股价
for i in tickers:
r_daily_mean = ((1+closeDf[i].pct_change()).prod())**(1/closeDf[i].shape[0])-1
annual_rets = (1+r_daily_mean)**252-1
print("%s'年化收益率:%s"%(i,str(round(annual_rets*100,2))+"%"))

maximum drawdowns
最大回撤率(Maximum Drawdown),它用于测量在投资组合价值中,在下一次峰值来到之前,最高点和最低点之间的最大单次下降。换言之,该值代表了基于某个策略的投资组合风险。
“最大回撤率是指在选定周期内任一历史时点往后推,产品净值走到最低点时的收益率回撤幅度的最大值。最大回撤用来描述买入产品后可能出现的最糟糕的情况。最大回撤是一个重要的风险指标,对于对冲基金和数量化策略交易,该指标比波动率还重要。” 最大回撤率超过了自己的风险承受范围,建议谨慎选择。
# 最大回撤率
def getMaxDrawdown(x):
j = np.argmax((np.maximum.accumulate(x) - x) / x)
if j == 0:
return 0
i = np.argmax(x[:j])
d = (x[i] - x[j]) / x[i] * 100
return d
for i in tickers:
MaxDrawdown = getMaxDrawdown(closeDf[i])
print("%s maximum drawdowns:%s"%(i,str(round(MaxDrawdown,2))+"%"))

# calmar率
# Calmar比率(Calmar Ratio) 描述的是收益和最大回撤之间的关系。计算方式为年化收益率与历史最大回撤之间的比率。
# Calmar比率数值越大,股票表现越好。
from pyfinance import TSeries # pip install pyfinance
from empyrical import sharpe_ratio,omega_ratio,alpha_beta,stats # pip install empyrical
def performance(i):
a = closeDf[i].pct_change()
s = a.values
idx = a.index
tss = TSeries(s, index=idx)
dd={}
dd['anlzd_ret']=str(round(tss.anlzd_ret()*100,2))+"%"
dd['cuml_ret']=str(round(tss.cuml_ret()*100,2))+"%"
dd['max_drawdown']=str(round(tss.max_drawdown()*100,2))+"%"
dd['sortino_ratio']=str(round(tss.sortino_ratio(freq=250),2))+"%"
dd['calmar_ratio']=str(round(tss.calmar_ratio()*100,2))+"%"
dd['sharpe_ratio'] = str(round(sharpe_ratio(tss)*100,2))+"%" # 夏普比率(Sharpe Ratio):风险调整后的收益率.计算投资组合每承受一单位总风险,会产生多少的超额报酬。
dd['annual_volatility'] = str(round(stats.annual_volatility(tss)*100,2))+"%" # 波动率
dd['omega_ratio'] = str(round(omega_ratio(tss)*100,2))+"%" # omega_ratio
df=pd.DataFrame(dd.values(),index=dd.keys(),columns = [i])
return df
dff = pd.DataFrame()
for i in tickers:
dd = performance(i)
dff = pd.concat([dff,dd],axis=1)
dff
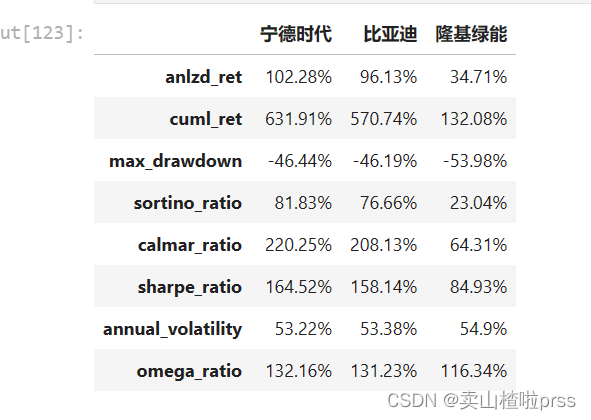
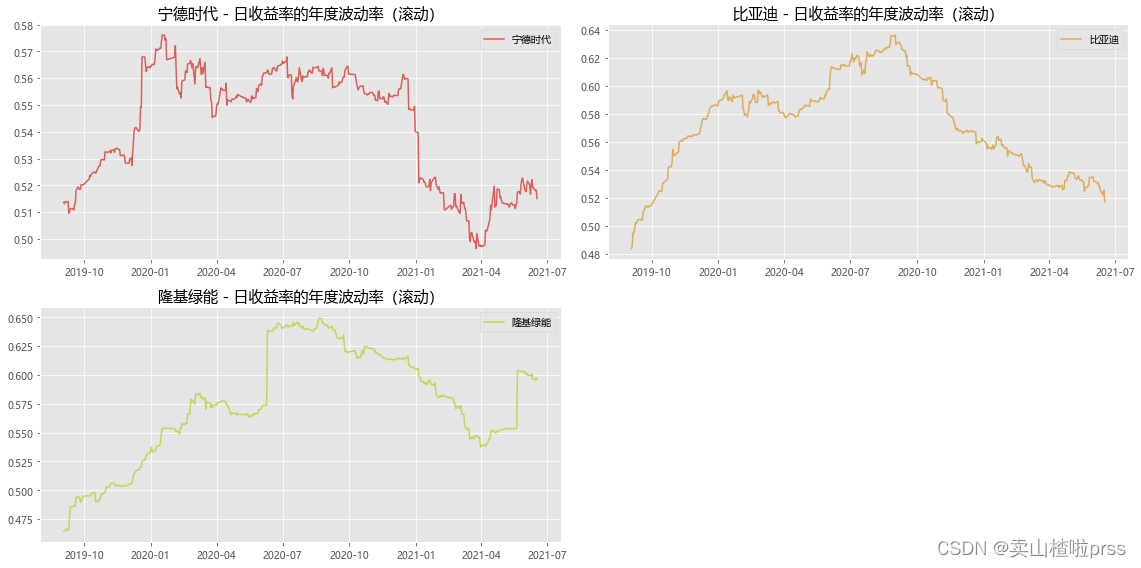
# 日收益率的年度波动率(滚动)
fig = plt.figure(figsize = (16,8))
for ii,jj in enumerate(tickers):
plt.subplot(2,2,ii+1)
vol = closeDf[jj].pct_change()[::-1].rolling(window=252,center=False).std()* np.sqrt(252)
plt.plot(vol,color=color_palette[ii],label=jj)
plt.title('%s - 日收益率的年度波动率(滚动)'%jj,size=15)
plt.legend()
plt.tight_layout()
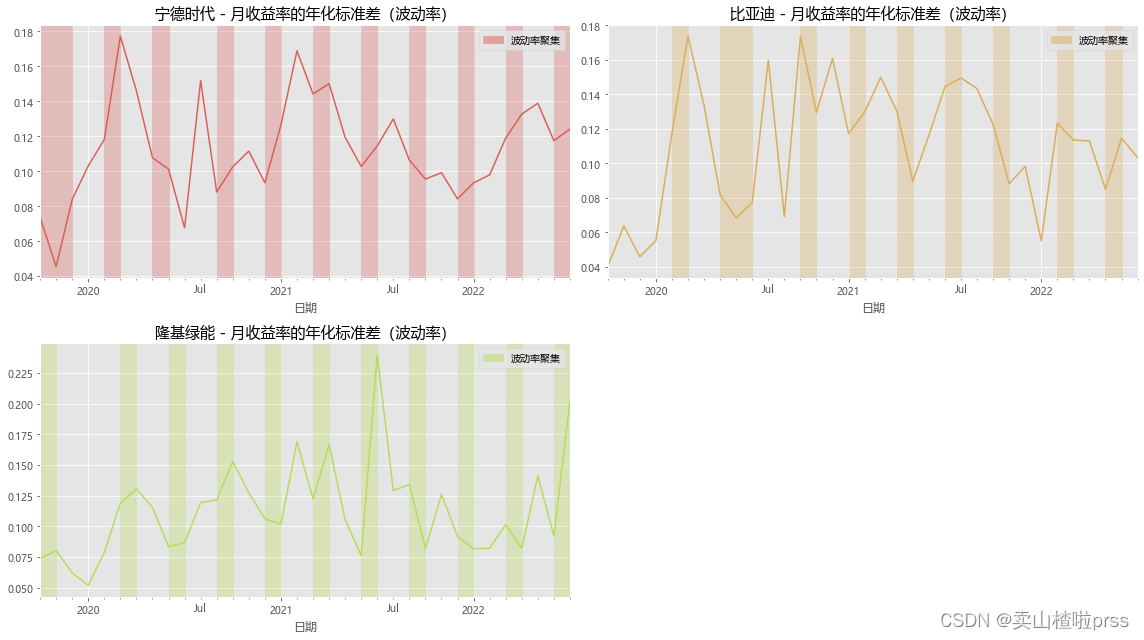
# Annualized standard deviation (volatility) of monthly return
# 月收益率的年化标准差(波动率)
# 实证研究表明,收益率标准差(波动率)存在一定的集聚现象,
# 即高波动率和低波动率往往会各自聚集在一起,并且高波动率和低波动率聚集的时期是交替出现的。
# 红色部门显示出,所有股票均存在一定的波动集聚现象。
fig = plt.figure(figsize = (16,9))
for ii,jj in enumerate(tickers):
plt.subplot(2,2,ii+1)
daily_ret=closeDf[jj].pct_change()
mnthly_annu = daily_ret.resample('M').std()* np.sqrt(12)
#plt.rcParams['figure.figsize']=[20,5]
mnthly_annu.plot(color=color_palette[ii],label=jj)
start_date=mnthly_annu.index[0]
end_date=mnthly_annu.index[-1]
plt.xticks(pd.date_range(start_date,end_date,freq='Y'),[str(y) for y in range(start_date.year+1,end_date.year+1)])
dates=mnthly_annu[mnthly_annu>0.07].index
for i in range(0,len(dates)-1,3):
plt.axvspan(dates[i],dates[i+1],color=color_palette[ii],alpha=.3)
plt.title('%s - 月收益率的年化标准差(波动率)'%jj,size=15)
labs = mpatches.Patch(color=color_palette[ii],alpha=.5, label="波动率聚集")
plt.legend(handles=[labs])
plt.tight_layout()
股票未来走势预测
模型一
import pandas as pd
import numpy as np
from statsmodels.tsa import holtwinters as hw
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
from statsmodels.graphics.gofplots import qqplot
import matplotlib.pyplot as plt
from statsmodels.tsa import arima_model
import warnings
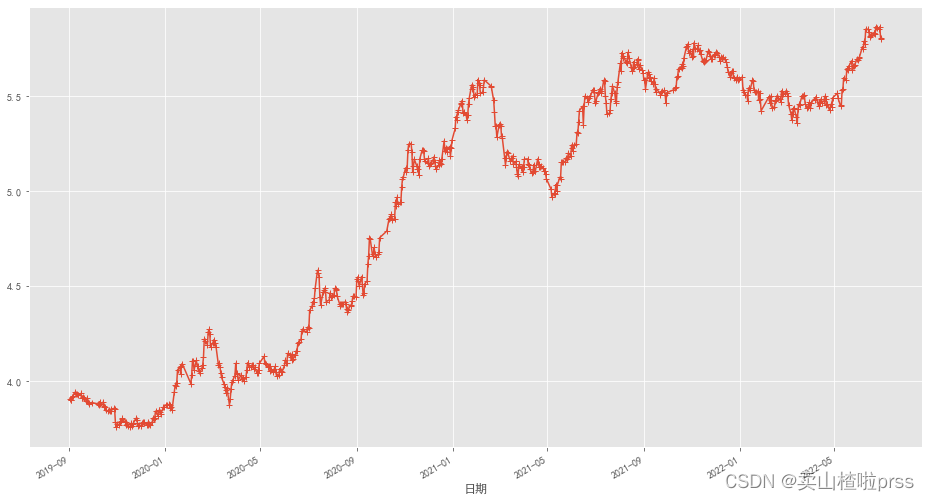
# 数据对数化
bonus_data = closeDf['比亚迪']
bonus_log = np.log(closeDf['比亚迪'])
bonus_log.plot(style='+-', figsize=(16, 9))
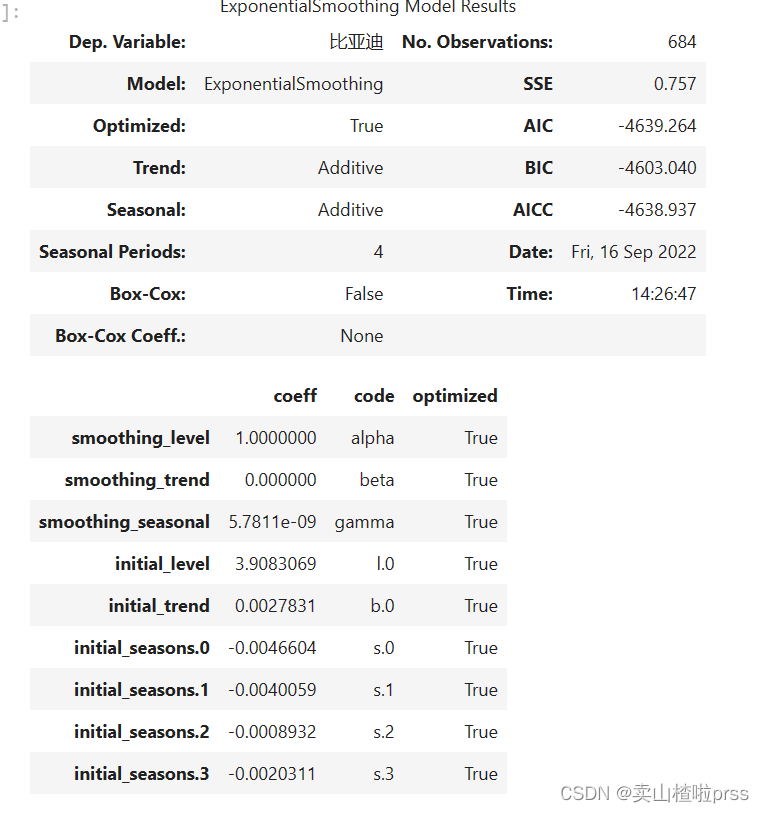
# 长期趋势、季节趋势:add
# 季节周期:季度
# seasonal_periods:季度数据为4,月度数据的为12,周周期数据为7
# trend、seasonal为add,任取一个时间段,数据增量为0
bonus_hw = hw.ExponentialSmoothing(bonus_log, trend='add', seasonal='add', seasonal_periods=4)
hw_fit = bonus_hw.fit()
hw_fit.summary()
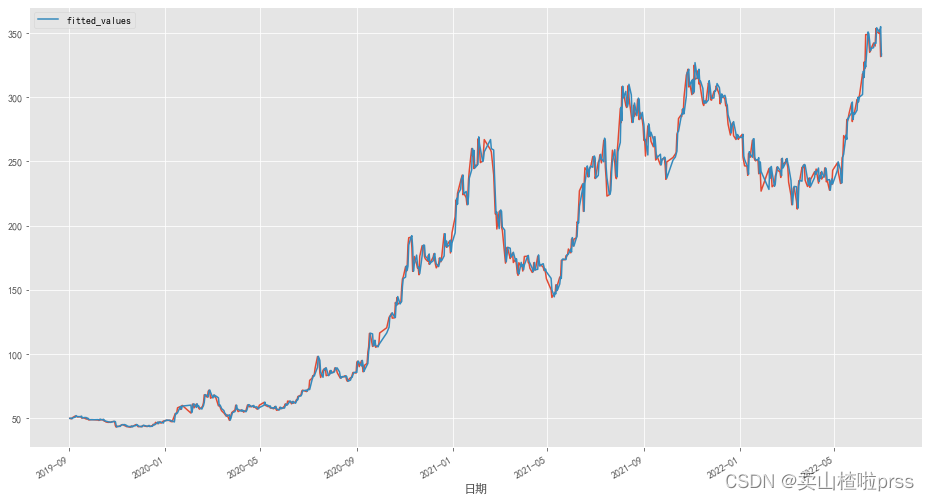
bonus_data.plot(figsize=(16, 9))
np.exp(hw_fit.fittedvalues).plot(label='fitted_values', legend=True)
bonus_forecast = np.exp(hw_fit.predict(start=len(bonus_data), end=len(bonus_data)+100))
print(bonus_forecast)

pd.DataFrame({
'origin': bonus_data,
'fitted': np.exp(hw_fit.fittedvalues),
'pred': bonus_forecast
}).plot(figsize=(16, 9),legend=True)
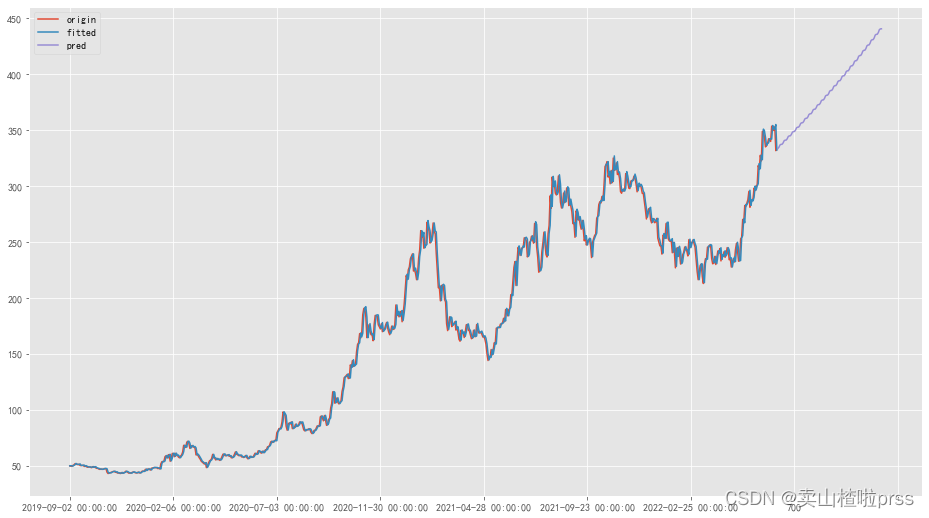
模型二
from autots import AutoTS
import matplotlib.pyplot as plt
import pandas as pd
#存放3家公司的收盘价
Df = pd.DataFrame()
#合并3家公司的收盘价
Df = pd.concat([Df,NDSD['trade_date'],NDSD['close'],BYD['close'],LJLN['close']],axis=1)
#重命名列名为公司名称
Df.columns=['日期','宁德时代','比亚迪','隆基绿能']
#将日期设置为行索引
Df['日期'] = pd.to_datetime(Df['日期'])
Df.set_index('日期',inplace=True)
Df = Df.sort_index(ascending=True)
Df = Df.reset_index()
Df
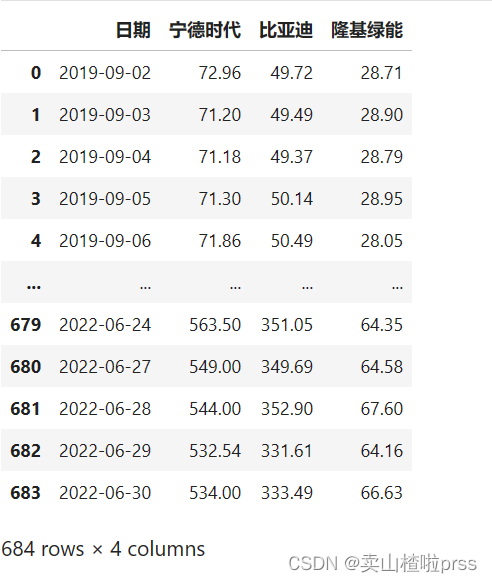
model = AutoTS(forecast_length=40, frequency='infer', ensemble='simple', drop_data_older_than_periods=100)
#model = AutoTS(forecast_length=46, score_type='rmse', time_interval='D', model_type='best')
model = model.fit(Df, date_col='日期', value_col='比亚迪', id_col=None)
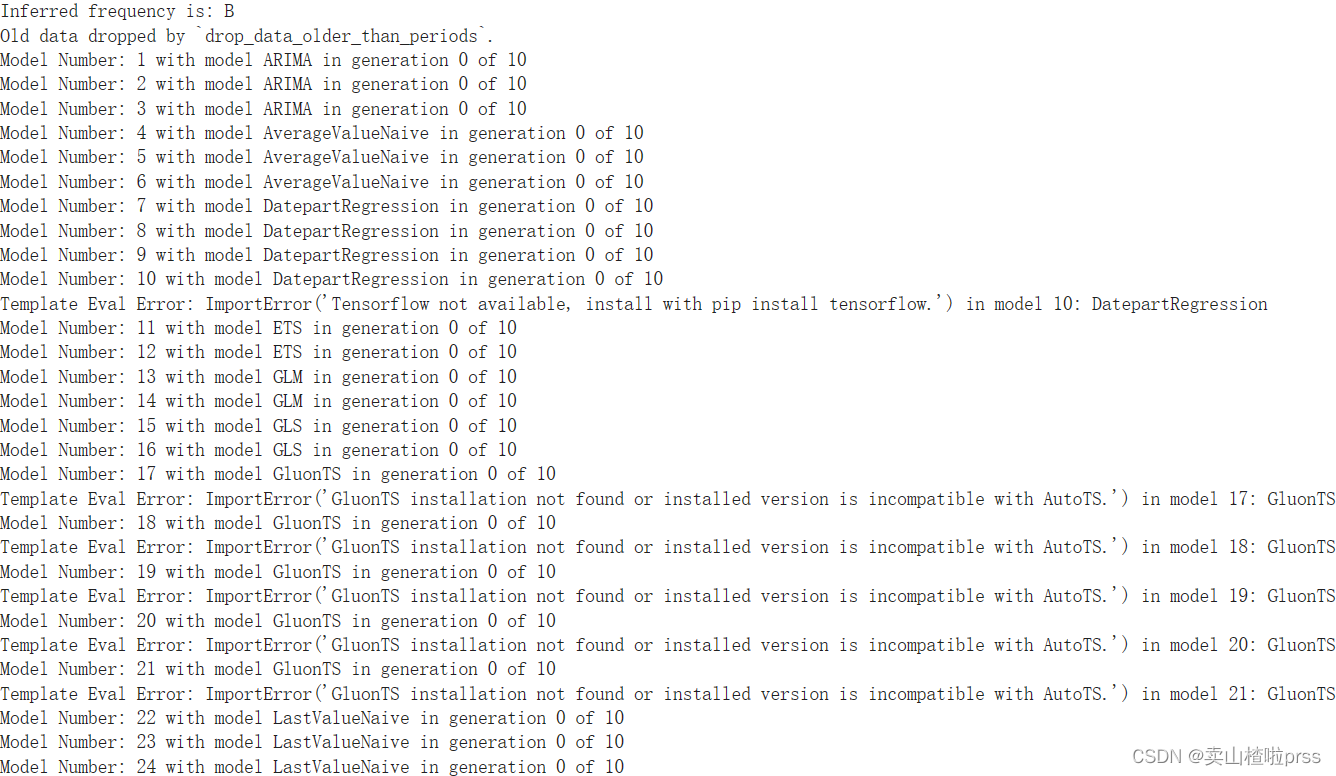
prediction = model.predict()
forecast = prediction.forecast
print("Stock Price Prediction of Apple")
print(forecast)
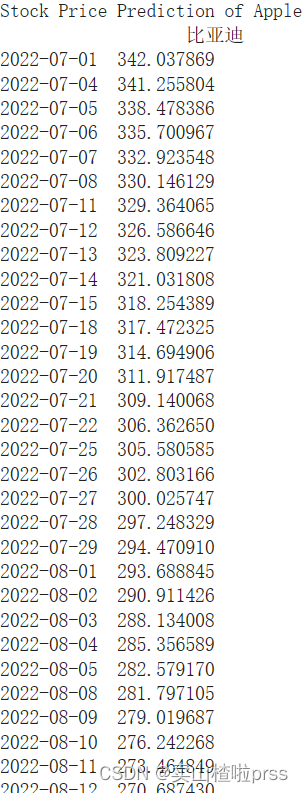
pd.DataFrame({
'origin': Df['比亚迪'],
'pred': forecast['比亚迪']
}).plot(figsize=(16, 9),legend=True)
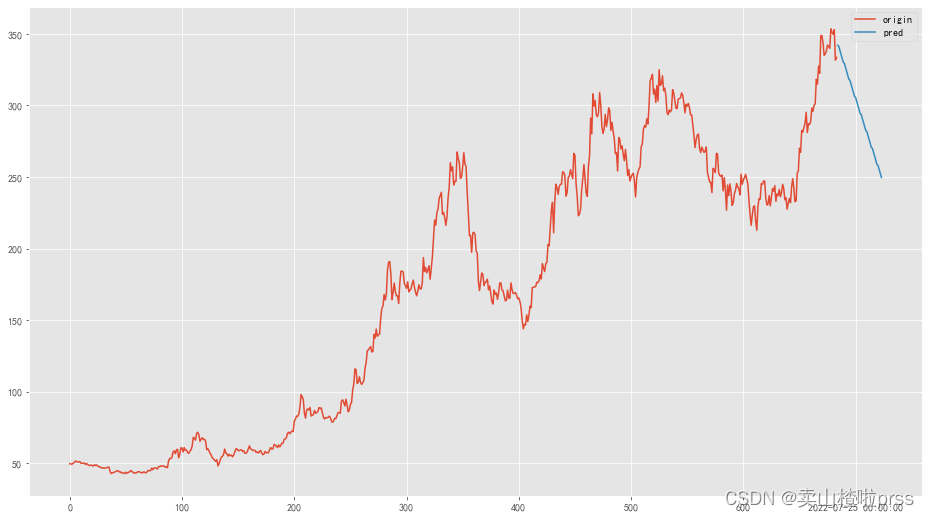
模型三
# TimeSeries从 Pandas DataFrame创建一个对象,并将其拆分为训练/验证系列:
import pandas as pd
import matplotlib.pyplot as plt
from darts import TimeSeries
from darts.models import ExponentialSmoothing
比亚迪
#closeDf = closeDf.reset_index()
df = closeDf[['比亚迪']]
df['日期'] = pd.date_range(start='2019-09-02',periods=684)
series = TimeSeries.from_dataframe(df, '日期', '比亚迪',fill_missing_dates=True)
train, val = series[:-50], series[-50:]
# 拟合指数平滑模型,并对验证系列的持续时间进行(概率)预测:
model = ExponentialSmoothing()
model.fit(train)
prediction = model.predict(len(val), num_samples=50)
# 绘制中位数、第 5 和第 95 个百分位数:
fig = plt.figure(figsize = (16,9))
series.plot()
prediction.plot(label='forecast', low_quantile=0.05, high_quantile=0.95)
plt.legend()
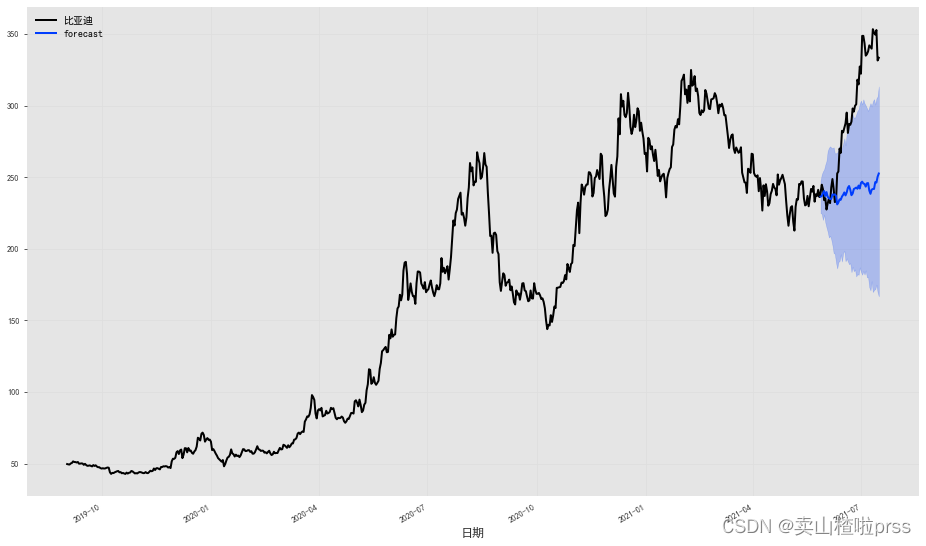
from darts.models import TCNModel
from darts.utils.likelihood_models import LaplaceLikelihood
model = TCNModel(
input_chunk_length=24,
output_chunk_length=12,
likelihood=LaplaceLikelihood(),
)
model.fit(train, epochs=150, verbose=True)

prediction = model.predict(len(val), num_samples=500)
# 绘制中位数、第 5 和第 95 个百分位数:
fig = plt.figure(figsize = (16,9))
series.plot()
prediction.plot(label='forecast', low_quantile=0.1, high_quantile=0.90)
plt.legend();
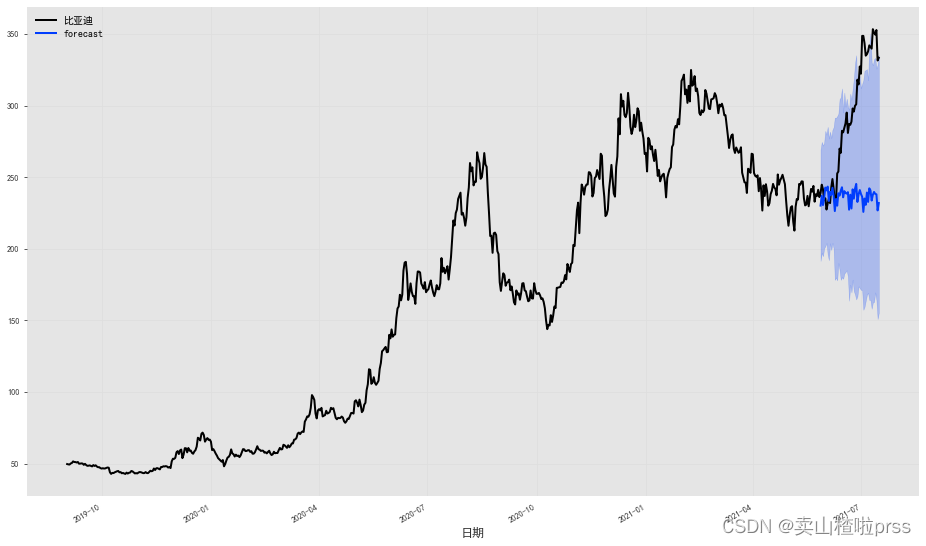
prediction
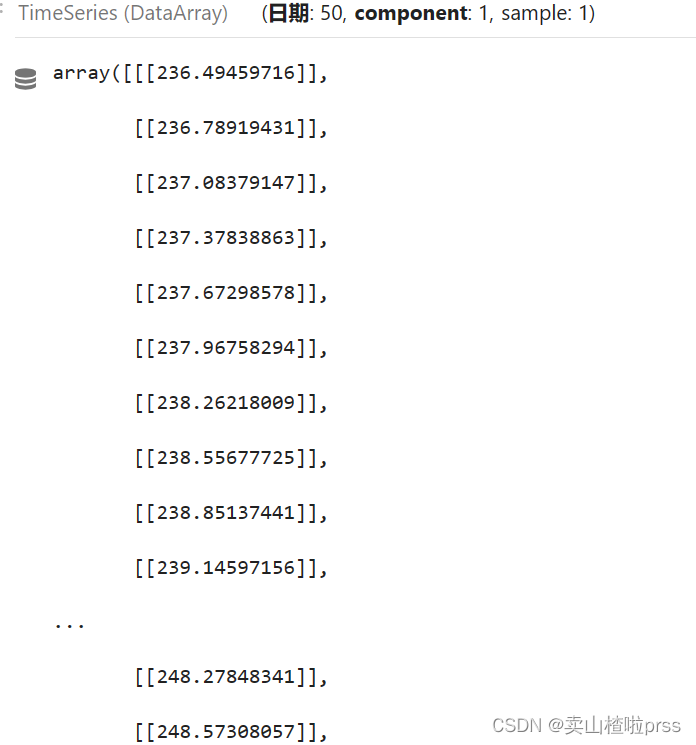
from darts.models import NaiveDrift
drift_model = NaiveDrift()
drift_model.fit(train)
prediction = drift_model.predict(len(val))
#prediction = model.predict(len(val), num_samples=500)
# 绘制中位数、第 5 和第 95 个百分位数:
fig = plt.figure(figsize = (16,9))
series.plot()
prediction.plot(label='forecast', low_quantile=0.1, high_quantile=0.90)
plt.legend();
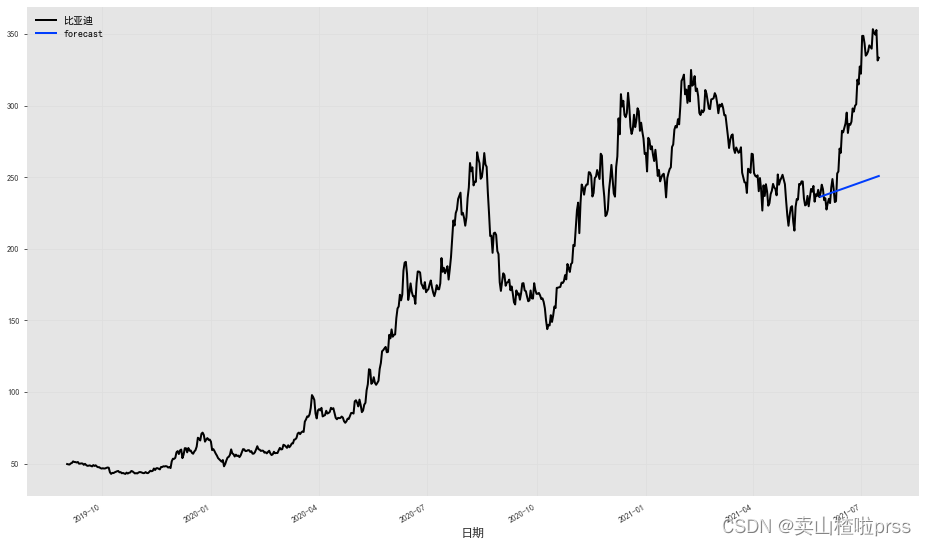
model = TCNModel(
input_chunk_length=24,
output_chunk_length=12,
likelihood=LaplaceLikelihood(prior_b=0.1),
)
model.fit(train, epochs=100, verbose=True);
prediction = model.predict(len(val), num_samples=500)
# 绘制中位数、第 5 和第 95 个百分位数:
fig = plt.figure(figsize = (16,9))
series.plot()
prediction.plot(label='forecast', low_quantile=0.05, high_quantile=0.95)
plt.legend();

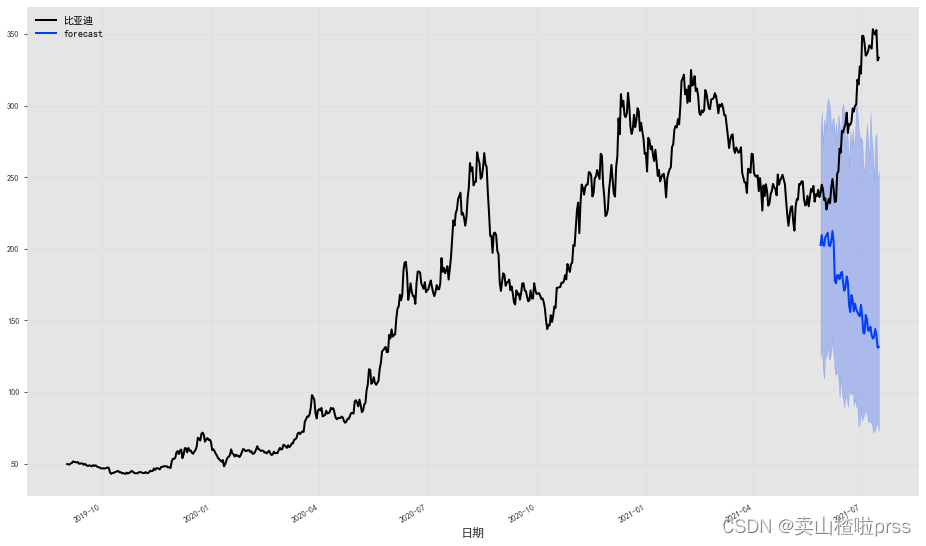
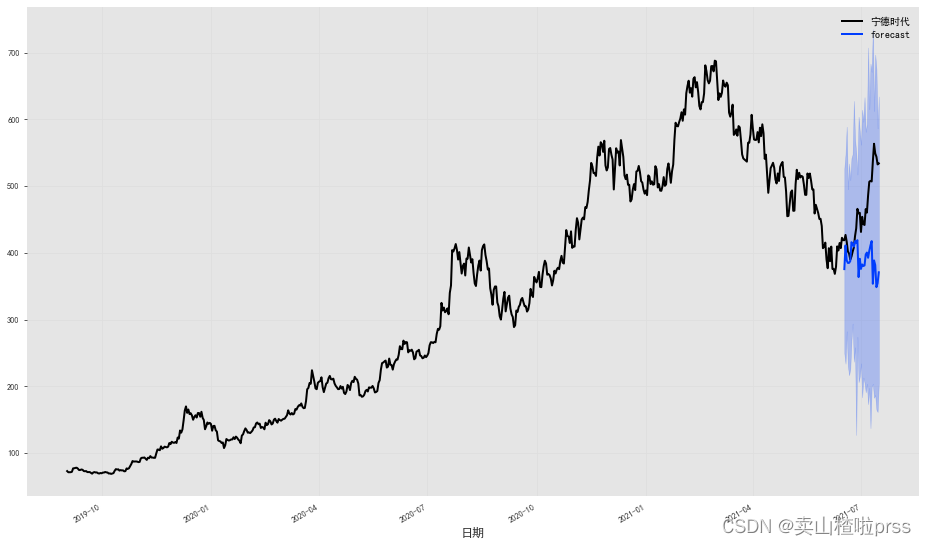
宁德时代
#closeDf = closeDf.reset_index()
df = closeDf[['宁德时代']]
df['日期'] = pd.date_range(start='2019-09-02',periods=684)
series = TimeSeries.from_dataframe(df, '日期', '宁德时代',fill_missing_dates=True)
train, val = series[:-30], series[-30:]
# 拟合指数平滑模型,并对验证系列的持续时间进行(概率)预测:
model = ExponentialSmoothing()
model.fit(train)
prediction = model.predict(len(val), num_samples=10)
# 绘制中位数、第 5 和第 95 个百分位数:
fig = plt.figure(figsize = (16,9))
series.plot()
prediction.plot(label='forecast', low_quantile=0.05, high_quantile=0.95)
plt.legend()
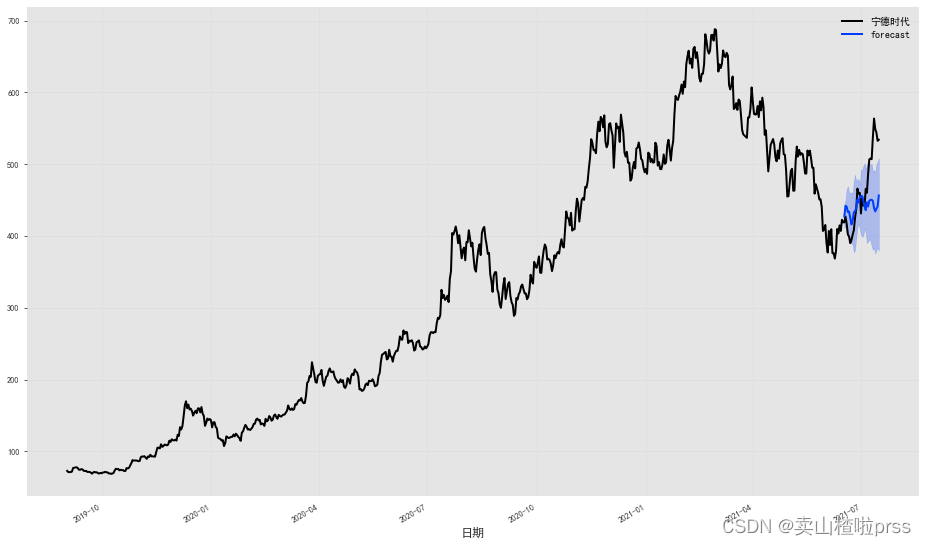
from darts.models import TCNModel
from darts.utils.likelihood_models import LaplaceLikelihood
model = TCNModel(
input_chunk_length=24,
output_chunk_length=12,
likelihood=LaplaceLikelihood(),
)
model.fit(train, epochs=50, verbose=True)

prediction = model.predict(len(val), num_samples=100)
# 绘制中位数、第 5 和第 95 个百分位数:
fig = plt.figure(figsize = (16,9))
series.plot()
prediction.plot(label='forecast', low_quantile=0.05, high_quantile=0.95)
plt.legend();
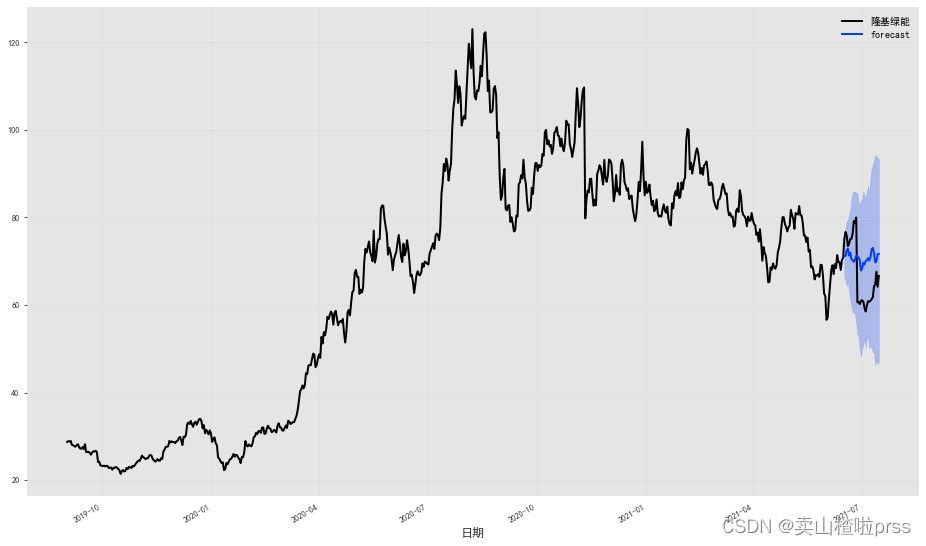
隆基绿能
#closeDf = closeDf.reset_index()
df = closeDf[['隆基绿能']]
df['日期'] = pd.date_range(start='2019-09-02',periods=684)
series = TimeSeries.from_dataframe(df, '日期', '隆基绿能',fill_missing_dates=True)
train, val = series[:-30], series[-30:]
# 拟合指数平滑模型,并对验证系列的持续时间进行(概率)预测:
model = ExponentialSmoothing()
model.fit(train)
prediction = model.predict(len(val), num_samples=50)
# 绘制中位数、第 5 和第 95 个百分位数:
fig = plt.figure(figsize = (16,9))
series.plot()
prediction.plot(label='forecast', low_quantile=0.05, high_quantile=0.95)
plt.legend()
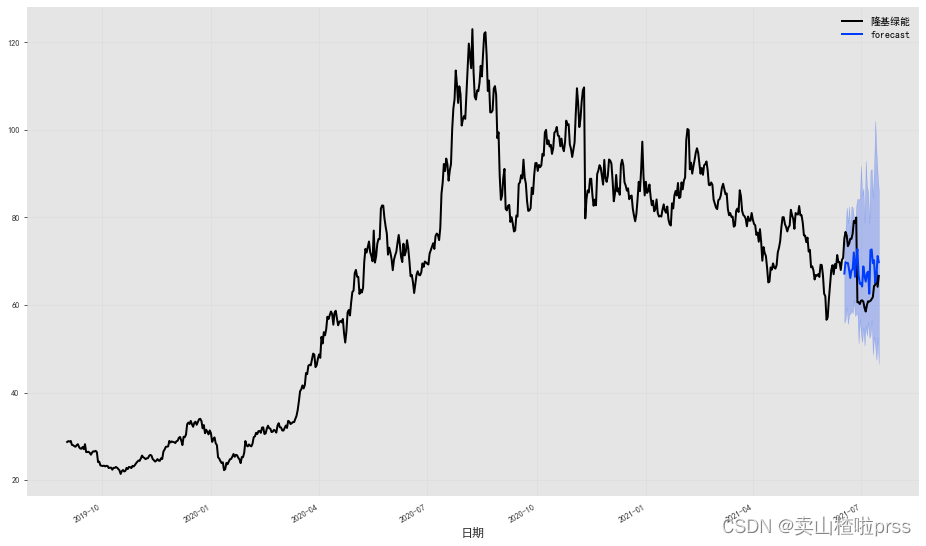
from darts.utils.likelihood_models import QuantileRegression
model2 = TCNModel(
input_chunk_length=24,
output_chunk_length=12,
likelihood=QuantileRegression([0.05, 0.1, 0.5, 0.9, 0.95]),
)
model2.fit(train, epochs=100, verbose=True);
prediction = model2.predict(len(val), num_samples=30)
# 绘制中位数、第 5 和第 95 个百分位数:
fig = plt.figure(figsize = (16,9))
series.plot()
prediction.plot(label='forecast', low_quantile=0.05, high_quantile=0.95)
plt.legend();
模型四
比亚迪
import pmdarima as pm
from pmdarima import model_selection
import matplotlib.pyplot as plt
import numpy as np
# 加载数据并将其拆分为单独的部分
data = closeDf['比亚迪']
train, test = model_selection.train_test_split(data, train_size=600)
# fit一些验证(cv)样本
arima = pm.auto_arima(train, start_p=1, start_q=1, d=0, max_p=5, max_q=5,
out_of_sample_size=60, suppress_warnings=True,
stepwise=True, error_action='ignore')
# 现在绘制测试集的结果和预测
preds, conf_int = arima.predict(n_periods=test.shape[0],
return_conf_int=True)
preds

fig, axes = plt.subplots(2, 1, figsize=(12, 8))
x_axis = np.arange(train.shape[0] + preds.shape[0])
axes[0].plot(x_axis[:train.shape[0]], train, alpha=0.75)
axes[0].scatter(x_axis[train.shape[0]:], preds, alpha=0.4, marker='o')
axes[0].scatter(x_axis[train.shape[0]:], test, alpha=0.4, marker='x')
axes[0].fill_between(x_axis[-preds.shape[0]:], conf_int[:, 0], conf_int[:, 1],
alpha=0.1, color='b')
# 填写在模型中"held out"样本的部分
axes[0].set_title("Train samples & forecasted test samples")
# 现在将实际样本添加到模型中并创建NEW预测
arima.update(test)
new_preds, new_conf_int = arima.predict(n_periods=10, return_conf_int=True)
new_x_axis = np.arange(data.shape[0] + 10)
axes[1].plot(new_x_axis[:data.shape[0]], data, alpha=0.75)
axes[1].scatter(new_x_axis[data.shape[0]:], new_preds, alpha=0.4, marker='o')
axes[1].fill_between(new_x_axis[-new_preds.shape[0]:],
new_conf_int[:, 0], new_conf_int[:, 1],
alpha=0.1, color='g')
axes[1].set_title("Added new observed values with new forecasts")
plt.show()







![[CKA]考试之Deployment管理pod扩缩容](https://img-blog.csdnimg.cn/ce4cf1dbf6c14d56add3248428b3bb7c.png)