300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
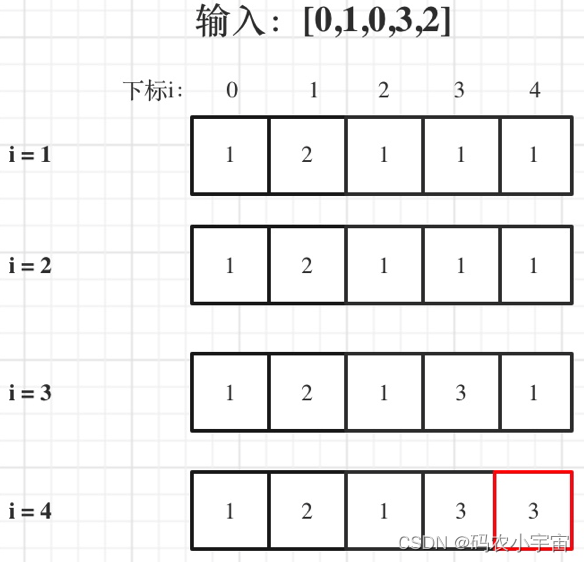
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
动归五部曲:
1. 确定dp数组和下标的含义
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
2. 状态转移方程
if(nums[i] > nums[j])dp[i] = max(dp[i], dp[j] + 1)
3. dp[i]初始化
任意dp[i]起始都是1
4. 确定遍历顺序
从前往后遍历
5. 举例推导dp数组
class Solution {
public int lengthOfLIS(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp,1);
for(int i = 0;i < nums.length;i ++){
for(int j = 0;j < i;j ++){
if(nums[i] > nums[j]){
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int res = 0;
for(int i = 0;i < dp.length;i ++){
res = Math.max(res, dp[i]);
}
return res;
}
}674. 最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
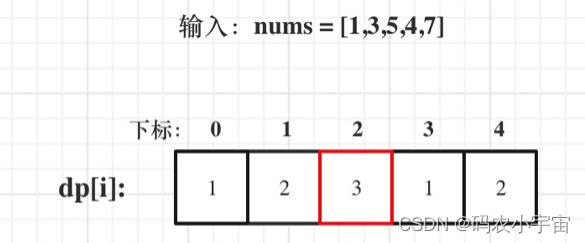
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。 尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。
动归五部曲:
1. 确定dp数组和下标的含义
dp[i]表示以下标i为结尾的连续递增的子序列的长度
2. 递推公式
dp[i] = dp[i - 1] + 1
3. dp数组初始化
dp[i]起始都为1
4. 遍历顺序
从前往后遍历
5. 举例推导dp数组
class Solution {
public int findLengthOfLCIS(int[] nums) {
int[] dp = new int[nums.length];
Arrays.fill(dp, 1);
for(int i = 0;i < nums.length - 1;i ++){
if(nums[i + 1] > nums[i]){
dp[i + 1] = dp[i] + 1;
}
}
int res = 0;
for(int i = 0;i < dp.length;i ++){
res = Math.max(res,dp[i]);
}
return res;
}
}718. 最长重复子数组
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3,2,1] 。
示例 2:
输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出:5
动归五部曲:
1. 确定dp数组和下标的含义
dp[i][j]表示以下标i-1结尾的序列和以下标j-1结尾的序列,最唱的公共子数组长度为dp[i][j]
2. 递推公式
dp[i][j] = dp[i - 1][j - 1] + 1
3. dp数组初始化
dp[i][j]起始全为1
4. 遍历顺序
从前往后
5. 举例推导dp数组
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int[][]dp = new int[nums1.length + 1][nums2.length + 1];
int res = 0;
for(int i = 1;i < nums1.length + 1;i ++){
for(int j = 1;j < nums2.length + 1;j ++){
if(nums1[i - 1] == nums2[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
res = Math.max(res, dp[i][j]);
}
}
}
return res;
}
}