前言

动态规划（Dynamic Programming，简称 DP）是一种解决多阶段决策过程最优化问题的方法。它是一种将复杂问题分解成重叠子问题的策略，通过维护每个子问题的最优解来推导出问题的最优解。

动态规划的主要思想是利用已求解的子问题的最优解来推导出更大问题的最优解，从而避免了重复计算。因此，动态规划通常采用自底向上的方式进行求解，先求解出小规模的问题，然后逐步推导出更大规模的问题，直到求解出整个问题的最优解。

动态规划通常包括以下几个基本步骤：

1. 定义状态：将问题划分为若干个子问题，并定义状态表示子问题的解；
2. 定义状态转移方程：根据子问题之间的关系，设计状态转移方程，即如何从已知状态推导出未知状态的计算过程；
3. 确定初始状态：定义最小的子问题的解；
4. 自底向上求解：按照状态转移方程，计算出所有状态的最优解；
5. 根据最优解构造问题的解。

动态规划可以解决许多实际问题，例如最短路径问题、背包问题、最长公共子序列问题、编辑距离问题等。同时，动态规划也是许多其他算法的核心思想，例如分治算法、贪心算法等。

动态规划是一种解决多阶段决策过程最优化问题的方法，它将复杂问题分解成重叠子问题，通过维护每个子问题的最优解来推导出问题的最优解。动态规划包括定义状态、设计状态转移方程、确定初始状态、自底向上求解和构造问题解等步骤。动态规划可以解决许多实际问题，也是其他算法的核心思想之一。

一、不同路径

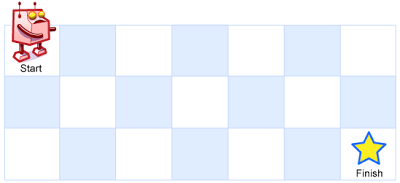
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

来源：力扣（LeetCode）。

1.1、思路

令 dp[i][j] 是到达 i, j 最多路径

动态方程：dp[i][j] = dp[i-1][j] + dp[i][j-1]

注意，对于第一行 dp[0][j]，或者第一列 dp[i][0]，由于都是在边界，所以只能为 1

时间复杂度：O(m∗n)

空间复杂度：O(m∗n)

优化：因为每次只需要 dp[i-1][j],dp[i][j-1]，所以只要记录这两个数。

1.2、代码实现

class Solution {
public:
    int uniquePaths(int m, int n) {
        long long ans = 1;
        for (int x = n, y = 1; y < m; ++x, ++y) {
            ans = ans * x / y;
        }
        return ans;
    }
};

二、不同路径 II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
   

示例2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

2.1、思路

递归思路：
假设我们定义到达右下角的走法数为 f(m,n), 因为右下角只能由它上方或者左方的格子走过去，因此可以很容易的写出递归求解式，即 f(m,n)=f(m−1,n)+f(m,n−1)，最后加上递归终止条件大功告成啦！

然而事情并木有结束～ 因为这样自底向上的递归会存在大量的重复计算，所以将其改写为在二维数组中自顶向下的递推即可，即 dp[i,j]=dp[i−1,j]+dp[i,j−1]。

1、状态定义：dp[i][j] 表示走到格子 (i,j) 的方法数。

2、状态转移：(i,j) 上有障碍物，则 dp[i][j] 值为 0，表示走到该格子的方法数为 0；否则网格 (i,j) 可以从网格 (i−1,j) 或者 网格 (i,j−1) 走过来，因此走到该格子的方法数为走到网格 (i−1,j) 和网格 (i,j−1) 的方法数之和，即 dp[i,j]=dp[i−1,j]+dp[i,j−1]。
状态转移方程如下：

3、初始条件：

• 第 1 列的格子只有从其上边格子走过去这一种走法，因此初始化 dp[i][0] 值为 1，存在障碍物时为 0；
• 第 1 行的格子只有从其左边格子走过去这一种走法，因此初始化 dp[0][j] 值为 1，存在障碍物时为 0。

2.2、代码实现

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int n = obstacleGrid.size(), m = obstacleGrid.at(0).size();
        vector <int> f(m);

        f[0] = (obstacleGrid[0][0] == 0);
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (obstacleGrid[i][j] == 1) {
                    f[j] = 0;
                    continue;
                }
                if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
                    f[j] += f[j - 1];
                }
            }
        }

        return f.back();
    }
};

时间复杂度：O(nm)，其中 n 为网格的行数，m 为网格的列数。我们只需要遍历所有网格一次即可。

空间复杂度：O(m)。利用滚动数组优化，我们可以只用 O(m) 大小的空间来记录当前行的 f 值。

三、最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

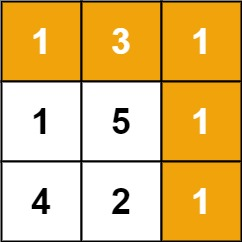
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

来源：力扣（LeetCode）。

3.1、思路

状态定义：设 dp 为大小 m×n 矩阵，其中 dp[i][j] 的值代表直到走到 (i,j) 的最小路径和。

由于路径的方向只能是向下或向右，因此网格的第一行的每个元素只能从左上角元素开始向右移动到达，网格的第一列的每个元素只能从左上角元素开始向下移动到达，此时的路径是唯一的，因此每个元素对应的最小路径和即为对应的路径上的数字总和。

对于不在第一行和第一列的元素，可以从其上方相邻元素向下移动一步到达，或者从其左方相邻元素向右移动一步到达，元素对应的最小路径和等于其上方相邻元素与其左方相邻元素两者对应的最小路径和中的最小值加上当前元素的值。由于每个元素对应的最小路径和与其相邻元素对应的最小路径和有关，因此可以使用动态规划求解。

创建二维数组 dp，与原始网格的大小相同，dpdp[i][j] 表示从左上角出发到 (i,j) 位置的最小路径和。显然，dp[0][0]=grid[0][0]。对于 dp 中的其余元素，通过以下状态转移方程计算元素值。

当 i>0 且 j=0 时，dp[i][0]=dp[i−1][0]+grid[i][0]。

当 i=0 且 j>0 时，dp[0][j]=dp[0][j−1]+grid[0][j]。

当 i>0 且 j>0 时，dp[i][j]=min(dp[i−1][j],dp[i][j−1])+grid[i][j]。

最后得到 dp[m−1][n−1] 的值即为从网格左上角到网格右下角的最小路径和。

3.3、代码实现

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        if (grid.size() == 0 || grid[0].size() == 0) {
            return 0;
        }
        int rows = grid.size(), columns = grid[0].size();
        auto dp = vector < vector <int> > (rows, vector <int> (columns));
        dp[0][0] = grid[0][0];
        for (int i = 1; i < rows; i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for (int j = 1; j < columns; j++) {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }
        for (int i = 1; i < rows; i++) {
            for (int j = 1; j < columns; j++) {
                dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[rows - 1][columns - 1];
    }
};

时间复杂度：O(mn)。

空间复杂度：O(mn)。

总结

动态规划（Dynamic Programming）是一种解决多阶段决策最优化问题的方法，它将复杂问题分解成重叠子问题并通过维护每个子问题的最优解来推导出问题的最优解。动态规划可以解决许多实际问题，例如最短路径问题、背包问题、最长公共子序列问题、编辑距离问题等。

动态规划的基本思想是利用已求解的子问题的最优解来推导出更大问题的最优解，从而避免了重复计算。它通常采用自底向上的方式进行求解，先求解出小规模的问题，然后逐步推导出更大规模的问题，直到求解出整个问题的最优解。

动态规划通常包括以下几个基本步骤：

1. 定义状态：将问题划分为若干个子问题，并定义状态表示子问题的解；
2. 定义状态转移方程：根据子问题之间的关系，设计状态转移方程，即如何从已知状态推导出未知状态的计算过程；
3. 确定初始状态：定义最小的子问题的解；
4. 自底向上求解：按照状态转移方程，计算出所有状态的最优解；
5. 根据最优解构造问题的解。

动态规划的时间复杂度通常为$O(n^2)$或$O(n^3)$，空间复杂度为O(n)，其中n表示问题规模。在实际应用中，为了减少空间复杂度，通常可以使用滚动数组等技巧来优化动态规划算法。