动态规划中级阶段

前言
一、最长回文子串
- 1.1、思路
- 1.2、代码实现
二、括号生成
- 2.1、思路
- 2.2、代码实现
三、跳跃游戏 II
- 3.2、思路
- 3.2、代码实现
总结

前言

动态规划（Dynamic Programming，简称 DP）是一种解决多阶段决策过程最优化问题的方法。它是一种将复杂问题分解成重叠子问题的策略，通过维护每个子问题的最优解来推导出问题的最优解。

动态规划的主要思想是利用已求解的子问题的最优解来推导出更大问题的最优解，从而避免了重复计算。因此，动态规划通常采用自底向上的方式进行求解，先求解出小规模的问题，然后逐步推导出更大规模的问题，直到求解出整个问题的最优解。

动态规划通常包括以下几个基本步骤：

定义状态：将问题划分为若干个子问题，并定义状态表示子问题的解；
定义状态转移方程：根据子问题之间的关系，设计状态转移方程，即如何从已知状态推导出未知状态的计算过程；
确定初始状态：定义最小的子问题的解；
自底向上求解：按照状态转移方程，计算出所有状态的最优解；
根据最优解构造问题的解。

动态规划可以解决许多实际问题，例如最短路径问题、背包问题、最长公共子序列问题、编辑距离问题等。同时，动态规划也是许多其他算法的核心思想，例如分治算法、贪心算法等。

动态规划是一种解决多阶段决策过程最优化问题的方法，它将复杂问题分解成重叠子问题，通过维护每个子问题的最优解来推导出问题的最优解。动态规划包括定义状态、设计状态转移方程、确定初始状态、自底向上求解和构造问题解等步骤。动态规划可以解决许多实际问题，也是其他算法的核心思想之一。

一、最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案。

示例 2：

输入：s = “cbbd”
输出：“bb”

来源：力扣（LeetCode）。

1.1、思路

对于一个子串而言，如果它是回文串，并且长度大于 2，那么将它首尾的两个字母去除之后，它仍然是个回文串。例如对于字符串 “ababa”，如果我们已经知道 “bab” 是回文串，那么 “ababa” 一定是回文串，这是因为它的首尾两个字母都是 “a”。

根据这样的思路，就可以用动态规划的方法解决本题。用 P(i,j) 表示字符串 s 的第 i 到 j 个字母组成的串（下文表示成 s[i:j]）是否为回文串：
在这里插入图片描述

这里的「其它情况」包含两种可能性：

s[i,j] 本身不是一个回文串；
i>j，此时 s[i,j] 本身不合法。

那么就可以写出动态规划的状态转移方程：
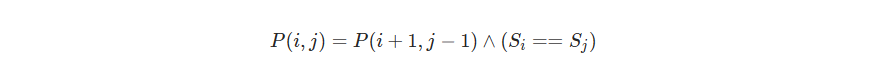
在这里插入图片描述
也就是说，只有 s[i+1:j−1] 是回文串，并且 s 的第 i 和 j 个字母相同时，s[i:j] 才会是回文串。

上文的所有讨论是建立在子串长度大于 2 的前提之上的，我们还需要考虑动态规划中的边界条件，即子串的长度为 1 或 2。对于长度为 1 的子串，它显然是个回文串；对于长度为 2 的子串，只要它的两个字母相同，它就是一个回文串。因此我们就可以写出动态规划的边界条件：

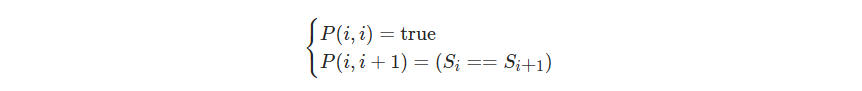
在这里插入图片描述

根据这个思路，我们就可以完成动态规划了，最终的答案即为所有 P(i,j)=true 中 j−i+1（即子串长度）的最大值。注意：在状态转移方程中，我们是从长度较短的字符串向长度较长的字符串进行转移的，因此一定要注意动态规划的循环顺序。

1.2、代码实现

#include <iostream>
#include <string>
#include <vector>

using namespace std;

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        if (n < 2) {
            return s;
        }

        int maxLen = 1;
        int begin = 0;
        // dp[i][j] 表示 s[i..j] 是否是回文串
        vector<vector<int>> dp(n, vector<int>(n));
        // 初始化：所有长度为 1 的子串都是回文串
        for (int i = 0; i < n; i++) {
            dp[i][i] = true;
        }
        // 递推开始
        // 先枚举子串长度
        for (int L = 2; L <= n; L++) {
            // 枚举左边界，左边界的上限设置可以宽松一些
            for (int i = 0; i < n; i++) {
                // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
                int j = L + i - 1;
                // 如果右边界越界，就可以退出当前循环
                if (j >= n) {
                    break;
                }

                if (s[i] != s[j]) {
                    dp[i][j] = false;
                } else {
                    if (j - i < 3) {
                        dp[i][j] = true;
                    } else {
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }

                // 只要 dp[i][L] == true 成立，就表示子串 s[i..L] 是回文，此时记录回文长度和起始位置
                if (dp[i][j] && j - i + 1 > maxLen) {
                    maxLen = j - i + 1;
                    begin = i;
                }
            }
        }
        return s.substr(begin, maxLen);
    }
};

时间复杂度： $O(n^2)$ 。
空间复杂度： $O(n^2)$

二、括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且有效的括号组合。

示例 1：

输入：n = 3
输出：[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”]

示例 2：

输入：n = 1
输出：[“()”]

来源：力扣（LeetCode）。

2.1、思路

当我们清楚所有 i<n 时括号的可能生成排列后，对与 i=n 的情况，我们考虑整个括号排列中最左边的括号。
它一定是一个左括号，那么它可以和它对应的右括号组成一组完整的括号 “( )”，我们认为这一组是相比 n-1 增加进来的括号。

那么，剩下 n-1 组括号有可能在哪呢？剩下的括号要么在这一组新增的括号内部，要么在这一组新增括号的外部（右侧）。

既然知道了 i<n 的情况，那我们就可以对所有情况进行遍历：

“(” + 【i=p时所有括号的排列组合】 + “)” + 【i=q时所有括号的排列组合】

其中 p + q = n-1，且 p q 均为非负整数。

事实上，当上述 p 从 0 取到 n-1，q 从 n-1 取到 0 后，所有情况就遍历完了。

注意：上述遍历是没有重复情况出现的，即当 (p1,q1)≠(p2,q2) 时，按上述方式取的括号组合一定不同。

2.2、代码实现

class Solution {
public:
    vector<string> generateParenthesis(int n) {
        //这里dp[i]表示的是i对括号形成的一堆合法的括号序列
        vector<vector<string>> dp(n + 1);
        // unordered_map<string, bool> f;
        //初始化
        dp[1].push_back("()");
        dp[0].push_back("");

        //从2开始计算
        for(int i = 2; i <= n; i ++)
        {
            // j从0开始枚举
            for(int j = 0; j < i; j ++)
            {
                for(auto s1: dp[j])
                {
                    string s4 = "(" + s1;
                    for(auto s2 : dp[i - 1 - j])
                    {
                        string s3 = s4 + ")" + s2;
                        dp[i].push_back(s3);
                    }
                }
            }
        }
        return dp[n];
    }
};

三、跳跃游戏 II

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

3.2、思路

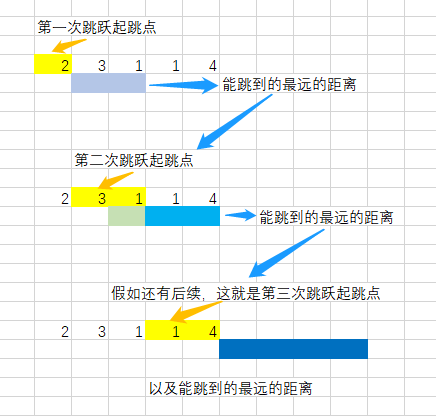
如果某一个作为起跳点的格子可以跳跃的距离是 3，那么表示后面 3 个格子都可以作为起跳点。可以对每一个能作为起跳点的格子都尝试跳一次，把能跳到最远的距离不断更新。
如果从这个起跳点起跳叫做第 1 次跳跃，那么从后面 3 个格子起跳都可以叫做第 2 次跳跃。
所以，当一次跳跃结束时，从下一个格子开始，到现在能跳到最远的距离，都是下一次跳跃的起跳点。对每一次跳跃用 for 循环来模拟；跳完一次之后，更新下一次起跳点的范围；在新的范围内跳，更新能跳到最远的距离。
记录跳跃次数，如果跳到了终点，就得到了结果。

3.2、代码实现

int jump(vector<int> &nums)
{
    int ans = 0;
    int start = 0;
    int end = 1;
    while (end < nums.size())
    {
        int maxPos = 0;
        for (int i = start; i < end; i++)
        {
            // 能跳到最远的距离
            maxPos = max(maxPos, i + nums[i]);
        }
        start = end;      // 下一次起跳点范围开始的格子
        end = maxPos + 1; // 下一次起跳点范围结束的格子
        ans++;            // 跳跃次数
    }
    return ans;
}

优化：

从上面代码观察发现，其实被 while 包含的 for 循环中，i 是从头跑到尾的。
只需要在一次跳跃完成时，更新下一次能跳到最远的距离。
并以此刻作为时机来更新跳跃次数。
就可以在一次 for 循环中处理。

int jump(vector<int>& nums)
{
    int ans = 0;
    int end = 0;
    int maxPos = 0;
    for (int i = 0; i < nums.size() - 1; i++)
    {
        maxPos = max(nums[i] + i, maxPos);
        if (i == end)
        {
            end = maxPos;
            ans++;
        }
    }
    return ans;
}