目录

最大似然估计

概念

最大似然估计原理

应用

最优化理论介绍 

最优化问题

迭代求解

---

最大似然估计

概念

最大似然估计（Maximum Likelihood Estimation，MLE）是统计学中一种常用的参数估计方法。它基于观测数据，通过寻找最大化参数的似然函数来估计参数的值。

最大似然估计法是由德国数学家高斯在1821年提出的 。 然而，这个方法常归功于英国统计学家费歇。因为费歇在1922年重新发现了这一方法，并首先研究了这种方法的一些性质。

在最大似然估计中，假设我们有一组观测数据，我们希望通过这些数据来估计一个未知参数的值。我们首先要建立一个参数化模型，该模型的形式取决于我们要估计的参数。然后，我们通过最大化似然函数来找到使观测数据出现的概率最大的参数值。

似然函数是指给定观测数据的条件下，参数取某个值的概率密度函数（连续型数据）或概率质量函数（离散型数据）。最大似然估计的核心思想是寻找使观测数据出现的概率最大化的参数值，也就是找到使似然函数取得最大值的参数。

具体而言，我们假设观测数据是独立同分布的，即每个观测值的产生不受其他观测值的影响，并且来自同一个分布。在最大似然估计中，我们将观测数据视为固定的，而参数是可变的。通过最大化似然函数，我们可以找到最有可能产生观测数据的参数值。

最大似然估计原理

最大似然估计通过已知结果去反推最大概率导致该结果的参数。

比如，现在已经得到样本值a1,a2,...an了，这表明取到这一样本值的概率比较大，而取到其

他样本值概率比较小。它提供了一种给定观察数据来评估模型参数的方法，即 “模型已定，

参数未知”，通过若干次试验，观察其结果，利用实验结果得到某些参数值能够使样本出现

的概率为最大。

应用

1. 参数估计：最大似然估计用于估计参数的值。通过最大化似然函数，我们可以找到在给定模型和观测数据下，最有可能生成观测数据的参数值。最大似然估计提供了一种基于数据的方法来推断未知参数的取值。

2. 假设检验：最大似然估计可以用于假设检验。我们可以通过比较两个具有不同参数值的模型的似然函数，来评估哪个模型更符合观测数据。通常，我们会计算似然比（likelihood ratio）作为比较的指标。较高的似然比表明一个模型相对于另一个模型更好地解释观测数据。

3. 模型选择：最大似然估计可以用于选择最合适的模型。假设我们有多个具有不同参数的模型，我们可以通过比较它们的似然函数或似然比来确定哪个模型最能解释观测数据。最大似然估计提供了一种准则来选择最优模型。

4. 预测与推断：最大似然估计可以用于预测和推断。通过估计模型的参数，我们可以使用模型来进行预测和推断。例如，在线性回归中，我们可以使用最大似然估计来估计回归系数，然后利用估计的模型进行未来观测值的预测。

最优化理论介绍 

最优化问题

最优化问题就是求 f(x)的最大值或者最小值，往往求最小值（比如损失函数的最小值），然

后找出对应的模型参数

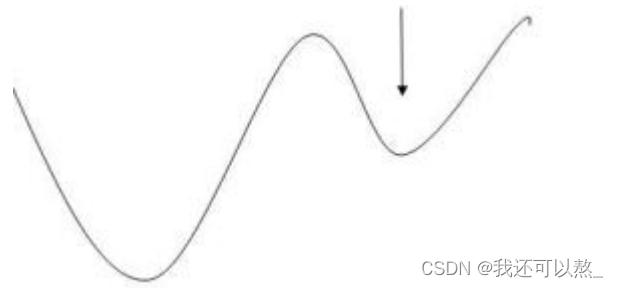
比如上面这个损失函数的图像，有两个局部最小值(也叫极小值)，我们需要找到的是最小

值，于是就分为两个步骤：

1. 先找到所有的局部最小值
2. 对所有的局部最小值再次进行比较，找到一个最小的，就是全局最小值了
3. 找出全局最小值位置对应的模型参数

迭代求解

如何从当前一个点移动到下一个点上面去，也就是怎么从 x~k~ 到 x~k+1~，迭代法是我们计

算数学中经常采用的一种方法。迭代的关键就是选择合适的搜索方向, 然后再确定步长，从

当前位置移动到下一个位置，判断损失函数是否达到最小值，从而找到对应的模型参数。