参考资料:
- https://zhuanlan.zhihu.com/p/114538417
- https://www.cnblogs.com/pinard/p/7243513.html
1 背景知识
1.1 统计语言模型
统计语言模型是基于语料库构建的概率模型,用来计算一个词串
W
=
(
w
1
,
w
2
,
⋯
,
w
T
)
W=(w_1,w_2,\cdots,w_T)
W=(w1,w2,⋯,wT) 构成句子的概率:
p
(
W
)
=
p
(
w
1
,
w
2
,
⋯
.
w
T
)
=
p
(
w
1
)
p
(
w
2
∣
w
1
)
⋯
p
(
w
T
∣
w
1
,
w
2
,
⋯
,
w
T
−
1
)
(乘法公式)
\begin{align} p(W)&=p(w_1,w_2,\cdots.w_T)\\ &=p(w_1)p(w_2|w_1)\cdots p(w_T|w_1,w_2,\cdots,w_{T-1})(乘法公式) \end{align}
p(W)=p(w1,w2,⋯.wT)=p(w1)p(w2∣w1)⋯p(wT∣w1,w2,⋯,wT−1)(乘法公式)
p
(
W
)
p(W)
p(W) 被称为语言模型,(2)式中的每个因子即为语言模型的参数。理论上,只要我们根据语料库计算出所有的模型参数,就能对很方便地计算出任意词串构成句子的概率,但由于参数过多,这种方法是不现实的。
1.2 N-gram模型
N-gram 模型的基本思想是做
n
−
1
n-1
n−1 阶 Markov 假设,即认为:
p
(
w
k
∣
w
1
,
w
2
,
⋯
,
w
k
−
1
)
=
p
(
w
k
∣
w
k
−
n
+
1
⋯
,
w
k
−
1
)
≈
c
o
u
n
t
(
w
k
−
n
+
1
⋯
,
w
k
−
1
,
w
k
)
c
o
u
n
t
(
w
k
−
n
+
1
⋯
,
w
k
−
1
)
(大数定律)
\begin{align} p(w_k|w_1,w_2,\cdots,w_{k-1})&=p(w_k|w_{k-n+1}\cdots,w_{k-1})\\ &\approx\frac{count(w_{k-n+1}\cdots,w_{k-1},w_k)}{count(w_{k-n+1}\cdots,w_{k-1})}(大数定律) \end{align}
p(wk∣w1,w2,⋯,wk−1)=p(wk∣wk−n+1⋯,wk−1)≈count(wk−n+1⋯,wk−1)count(wk−n+1⋯,wk−1,wk)(大数定律)
其中,
c
o
u
n
t
(
W
)
count(W)
count(W) 表示词串
W
W
W 在语料库中出现的次数。
需要注意的是:根据实际意义,即使 c o u n t ( w k − n + 1 ⋯ , w k − 1 , w k ) = 0 count(w_{k-n+1}\cdots,w_{k-1},w_k)=0 count(wk−n+1⋯,wk−1,wk)=0,也不能认为 p ( w k ∣ w k − n + 1 ⋯ , w k − 1 ) = 0 p(w_k|w_{k-n+1}\cdots,w_{k-1})=0 p(wk∣wk−n+1⋯,wk−1)=0 ;同理,即使 c o u n t ( w k − n + 1 ⋯ , w k − 1 , w k ) = c o u n t ( w k − n + 1 ⋯ , w k − 1 ) {count(w_{k-n+1}\cdots,w_{k-1},w_k)}={count(w_{k-n+1}\cdots,w_{k-1})} count(wk−n+1⋯,wk−1,wk)=count(wk−n+1⋯,wk−1),也不能认为 p ( w k ∣ w k − n + 1 ⋯ , w k − 1 ) = 1 p(w_k|w_{k-n+1}\cdots,w_{k-1})=1 p(wk∣wk−n+1⋯,wk−1)=1,故 N-gram 模型往往需要进行平滑处理。
但这种方法的参数仍然很多,所以我们可以考虑构建一个函数
F
=
(
w
,
c
o
n
t
e
x
t
(
w
)
,
θ
)
F=(w,{\rm context}(w),\theta)
F=(w,context(w),θ),通过极大似然估计的方式估计出参数
θ
\theta
θ:
L
(
θ
)
=
∑
w
∈
C
log
p
(
w
∣
c
o
n
t
e
x
t
(
w
)
,
θ
)
L(\theta)=\sum\limits_{w\in C}\log p(w|{\rm context}(w),\theta)
L(θ)=w∈C∑logp(w∣context(w),θ)
其中 C 为语料库。这样以来,所有条件概率的计算都可以通过计算
F
(
w
,
c
o
n
t
e
x
t
(
w
)
,
θ
^
)
F(w,{\rm context}(w),\hat\theta)
F(w,context(w),θ^) 来完成。显然,如何构建
F
F
F 成为了这一方法的关键问题。
直白地说,就是从语料库中选择词及其上下文,让由上下文通过模型推出词的概率最大。
2 词向量
词向量:对词典中的任意词 w w w,指定一个固定长度的向量 v ( w ) ∈ R m v(w)\in\mathbb R^m v(w)∈Rm。
2.1 独热编码
One-Hot 编码的向量长度为词典大小,向量中只有一个 1 1 1 ,位置与该词在词典中的位置相对应。
这样的编码主要有如下问题:
- 向量维数过大。
- 无法表现词之间的相关性。
2.2 Distributed Representation
基本想法:将词映射到一个向量空间,并在向量空间中引入“距离”,用以刻画词之间的关联程度。
Word2Vec 就是生成词向量的经典模型。
3 Word2Vec
Word2Vec 是轻量级的神经网络,其模型仅仅包括输入层、隐藏层和输出层,主要包括 CBOW 和 Skip-gram 模型
3.1 Simple CBOW Model
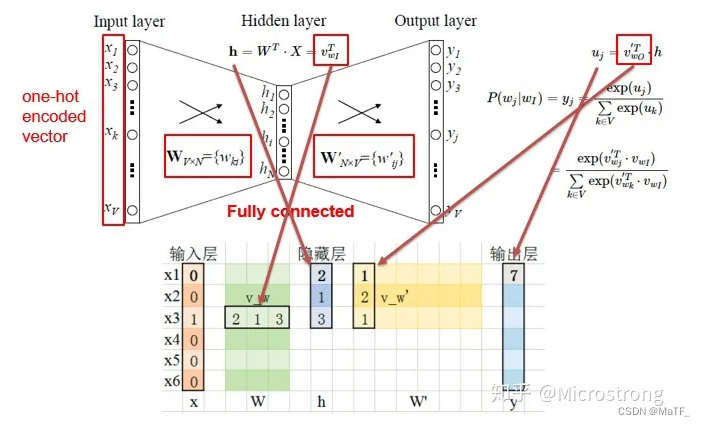
如上图所示:
- 输入为单词的独热编码,与输入层与隐藏层之间的权重矩阵相乘( W T X W^TX WTX ),相当于得到权重矩阵中某一行的转置。
- 隐藏层再和隐藏层与输出层之间的权重矩阵相乘( ( W ′ ) T h (W')^{T}h (W′)Th ),得到输出层 u u u
- 将输出向量的每一个分量经过 sotfmax 函数归一化,令概率最大的那个分量为 1 ,其余为 0 ,得到的向量即为预测词的独热编码。
由于该模型在输出层需要对每一个分量进行 softmax 函数归一化,而输出层的分量数由于词典的词数相同,故其计算量很大。
3.2 基于Hierarchical Softmax的CBOW
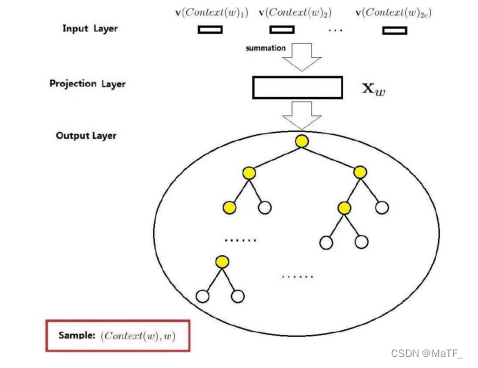
这部分建议直接看参考资料 2