Sunday 算法

Sunday算法是Daniel M.Sunday于1990年提出的字符串模式匹配。其核心思想是：在匹配过程中，模式串发现不匹配时，算法能跳过尽可能多的字符以进行下一步的匹配，从而提高了匹配效率。

一、匹配机制

匹配机制非常容易理解：

目标字符串 String
模式串 Pattern
当前查询索引 idx （初始为 0）
待匹配字符串 str_cut : String [ idx : idx + len(Pattern) ]

每次匹配都会从 目标字符串中 提取 待匹配字符串 与 模式串 进行匹配：

若匹配，则返回当前 idx
不匹配，则查看 待匹配字符串 的后一位字符 c：
1. 若 c 存在于 Pattern 中，则 idx = idx + 偏移表[c]
2. 否则，idx = idx + len(pattern)

循环上述匹配过程直到 idx + len(pattern) > len(String)

二、偏移表

偏移表的作用是存储每一个在 模式串 中出现的字符，在 模式串 中出现的最右位置到尾部的距离 +1，例如 aab：

a 的偏移位就是 len(pattern)-1 = 2
b 的偏移位就是 len(pattern)-2 = 1
其他的均为 len(pattern)+1 = 4

综合一下：

$\begin{cases}m-max\{i<m|p[i]=w\}\quad \text {if w is in P[0..m-1]} \\ m+1\quad \text{otherwise} \end{cases}$

三、举例

String: checkthisout Pattern: this

Step 1:
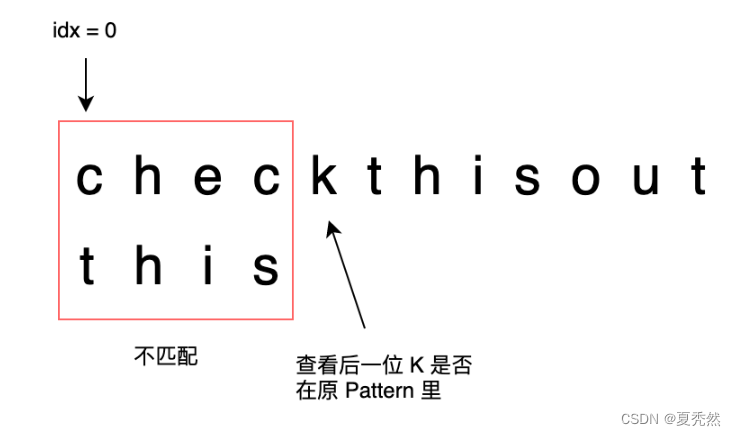
在这里插入图片描述

idx = 0
待匹配字符串为：chec
因为 chec != this
所以查看 chec 的下一个字符 k
k 不在 Pattern 里
所以查看 偏移表，idx = idx + 5

Step 2:
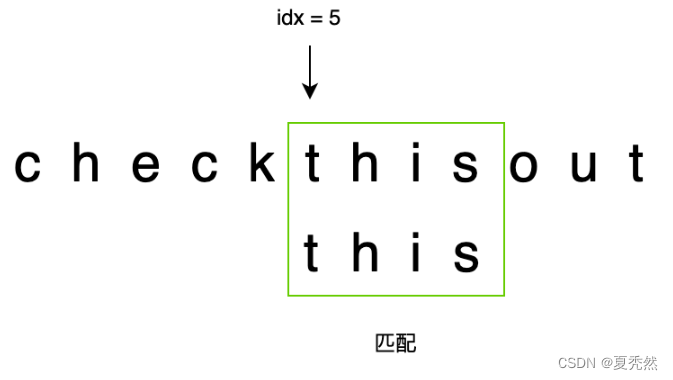
在这里插入图片描述

idx = 5
待匹配字符串为：this
因为 this == this
匹配，所以返回 5

四、算法分析

时间复杂度： 最坏情况 $O (n m)$ ，平均情况 $O (n)$
空间复杂度： $O (c)$ ，c为位移表长度

五、代码实现

class Solution:
    def strStr(self, haystack, needle):
        haystack_length = len(haystack)
        needle_length = len(needle)
        return self.sunday(haystack, haystack_length, needle, needle_length)

    def sunday(self, s, s_len, p, p_len):
        bc_move_dict = self.badChatMove(p, p_len)
        now = 0
        # 如果匹配字符的位置到达两字符串长度的差值，则不可能存在匹配字串，则退出循环
        while now <= s_len - p_len:
        	# 比对当前位置的子串是否和模式串匹配
            if s[now: now+p_len] == p:
                return now
            # 如果以及到达两字符串长度的差值，那么这将是最后一个可能匹配到的子串
            # 经过上面的比对没有匹配的话，直接返回-1
            if now == s_len - p_len:
                return -1
            # 更新下标，如果模式串不包含匹配串后面的第一个字符，则移动 p_len+1 个位数
            now += bc_move_dict.get(s[now+p_len], p_len+1)
        return -1
	
	# 坏字符移动数量计算
    def badChatMove(self, p, p_len):
        bc_move_dict = dict()
        for i in range(p_len):
        	# 记录该字符在模式串中出现的最右位置到尾部的距离+1
            bc_move_dict[p[i]] = p_len - i
        return bc_move_dict