文章目录
CSDN提示我字数太多,一篇发不下,只好拆分开x2。。。
关于
- 标准DH模型
- 改进DH模型
- 机器人正运动学
的相关内容详见第一篇文章:
→→→【工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(一)】
关于
- 机器人逆运动学求解 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2、 θ 3 \theta_3 θ3
的内容详见第二篇文章
→→→【工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(二)】
❤ 2023.6.27 ❤
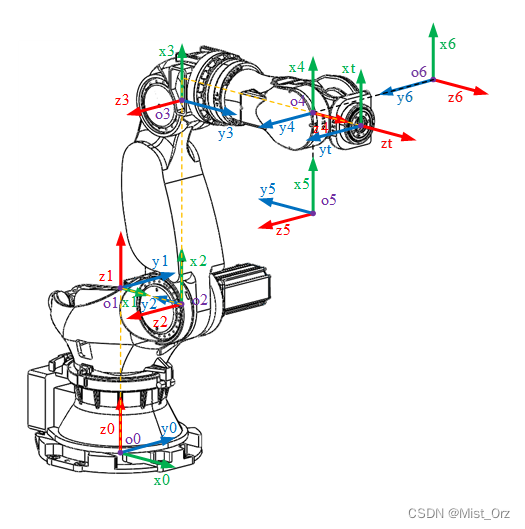
机器人逆运动学
△ 代数解求 θ 4 \theta_4 θ4、 θ 5 \theta_5 θ5、 θ 6 \theta_6 θ6
○ 求解 θ 4 \theta_4 θ4
将式末端位姿描述矩阵两边同时左
3
2
T
−
1
2
1
T
−
1
1
0
T
−
1
{{_3^2}T}^{-1}\ {{_2^1}T}^{-1}\ {{_1^0}T}^{-1}
32T−1 21T−1 10T−1得:
3
2
T
−
1
2
1
T
−
1
1
0
T
−
1
6
0
T
=
4
3
T
(
θ
4
)
5
4
T
(
θ
5
)
6
5
T
(
θ
6
)
\ {{_3^2}T}^{-1}\ {{_2^1}T}^{-1}\ {{_1^0}T}^{-1}\ _6^0T=_4^3T\left(\theta_4\right)\ _5^4T\left(\theta_5\right)\ _6^5T\left(\theta_6\right)
32T−1 21T−1 10T−1 60T=43T(θ4) 54T(θ5) 65T(θ6)
其中:
3
2
T
−
1
2
1
T
−
1
1
0
T
−
1
=
[
c
1
c
23
s
1
c
23
s
23
−
a
1
c
23
−
d
1
s
23
−
a
2
c
3
−
c
1
s
23
−
s
1
s
23
c
23
a
1
s
23
−
d
1
c
23
+
a
2
s
3
s
1
−
c
1
0
0
0
0
0
1
]
\ {{_3^2}T}^{-1}\ {{_2^1}T}^{-1}\ {{_1^0}T}^{-1}=\left[\begin{matrix}c_1c_{23}&s_1c_{23}&s_{23}&-a_1c_{23}-d_1s_{23}-a_2c_3\\-c_1s_{23}&-s_1s_{23}&c_{23}&a_1s_{23}-d_1c_{23}+a_2s_3\\s_1&-c_1&0&0\\0&0&0&1\\\end{matrix}\right]
32T−1 21T−1 10T−1=
c1c23−c1s23s10s1c23−s1s23−c10s23c2300−a1c23−d1s23−a2c3a1s23−d1c23+a2s301
4
3
T
(
θ
4
)
5
4
T
(
θ
5
)
6
5
T
(
θ
6
)
=
[
c
4
c
5
c
6
−
s
4
s
6
−
c
6
s
4
−
c
4
c
5
s
6
c
4
s
5
a
3
c
6
s
5
−
s
5
s
6
−
c
5
−
d
4
c
4
s
6
+
c
5
c
6
s
4
c
4
c
6
−
c
5
s
4
s
6
s
4
s
5
0
0
0
0
1
]
{_4^3}T\left(\theta_4\right)\ _5^4T\left(\theta_5\right)\ _6^5T\left(\theta_6\right)=\left[\begin{matrix}c_4c_5c_6-s_4s_6&-c_6s_4-c_4c_5s_6&c_4s_5&a_3\\c_6s_5&-s_5s_6&-c_5&-d_4\\c_4s_6+c_5c_6s_4&c_4c_6-c_5s_4s_6&s_4s_5&0\\0&0&0&1\\\end{matrix}\right]
43T(θ4) 54T(θ5) 65T(θ6)=
c4c5c6−s4s6c6s5c4s6+c5c6s40−c6s4−c4c5s6−s5s6c4c6−c5s4s60c4s5−c5s4s50a3−d401
- ※ 计算过程
syms Q1 Q2 Q3 Q4 Q5 Q6 d1 d4 dt a1 a2 a3 nx ny nz ox oy oz ax ay az px py pz
%ZK-500连杆间齐次变换矩阵
T_01 =[ cos(Q1), -sin(Q1), 0, 0
sin(Q1), cos(Q1), 0, 0
0, 0, 1, d1
0, 0, 0, 1];
T_12 =[ cos(Q2), -sin(Q2), 0, a1
0, 0, -1, 0
sin(Q2), cos(Q2), 0, 0
0, 0, 0, 1];
T_23 =[ cos(Q3), -sin(Q3), 0, a2
sin(Q3), cos(Q3), 0, 0
0, 0, 1, 0
0, 0, 0, 1];
T_34 =[ cos(Q4), -sin(Q4), 0, a3
0, 0, -1, -d4
sin(Q4), cos(Q4), 0, 0
0, 0, 0, 1];
T_45 =[ cos(Q5), -sin(Q5), 0, 0
0, 0, 1, 0
-sin(Q5), -cos(Q5), 0, 0
0, 0, 0, 1];
T_56 =[ cos(Q6), -sin(Q6), 0, 0
0, 0, -1, 0
sin(Q6), cos(Q6), 0, 0
0, 0, 0, 1];
T_6t=[ 1 0 0 0
0 1 0 0
0 0 1 dt
0 0 0 1];
% 计算T_06和T_16的逆矩阵
T_06=[nx ox ax px;ny oy ay py;nz oz az pz;0 0 0 1];
T_03=T_01*T_12*T_23;
T_36=T_34*T_45*T_56;
% 计算T_01的逆矩阵
T_03_inv = inv(T_03);
T_03_inv=simplify(T_03_inv)
T_36=simplify(T_36)
结果
T_03_inv =
[ cos(Q2 + Q3)*cos(Q1), cos(Q2 + Q3)*sin(Q1), sin(Q2 + Q3), - a1*cos(Q2 + Q3) - d1*sin(Q2 + Q3) - a2*cos(Q3)]
[-sin(Q2 + Q3)*cos(Q1), -sin(Q2 + Q3)*sin(Q1), cos(Q2 + Q3), a1*sin(Q2 + Q3) - d1*cos(Q2 + Q3) + a2*sin(Q3)]
[ sin(Q1), -cos(Q1), 0, 0]
[ 0, 0, 0, 1]
T_36 =
[cos(Q4)*cos(Q5)*cos(Q6) - sin(Q4)*sin(Q6), - cos(Q6)*sin(Q4) - cos(Q4)*cos(Q5)*sin(Q6), cos(Q4)*sin(Q5), a3]
[ cos(Q6)*sin(Q5), -sin(Q5)*sin(Q6), -cos(Q5), -d4]
[cos(Q4)*sin(Q6) + cos(Q5)*cos(Q6)*sin(Q4), cos(Q4)*cos(Q6) - cos(Q5)*sin(Q4)*sin(Q6), sin(Q4)*sin(Q5), 0]
[ 0, 0, 0, 1]
matlab真好用。。。。
令元素(1,3)和(3,3)等号左右相等得到:
a
x
c
1
c
23
+
a
y
s
1
c
23
+
a
z
s
23
=
c
4
s
5
a
x
s
1
−
a
y
c
1
=
s
4
s
5
a_xc_1c_{23}+a_ys_1c_{23}+a_zs_{23}=c_4s_5\\ a_xs_1-a_yc_1=s_4s_5
axc1c23+ays1c23+azs23=c4s5axs1−ayc1=s4s5
计算过程见前面求 θ 2 \theta_2 θ2的内容
→→→跳转到 计算过程
化简是手动化简的。。。
记
h
1
=
a
x
c
1
c
23
+
a
y
s
1
c
23
+
a
z
s
23
h
2
=
a
x
s
1
−
a
y
c
1
h_1=a_xc_1c_{23}+a_ys_1c_{23}+a_zs_{23}\\ h_2=a_xs_1-a_yc_1
h1=axc1c23+ays1c23+azs23h2=axs1−ayc1
将式()等号两边取平方和可得
s
5
2
=
h
1
2
+
h
2
2
s_5^2=h_1^2+h_2^2
s52=h12+h22
虽然这里通过
θ 5 = arcsin ( ± ( h 1 2 + h 2 2 ) ) \theta_5=\arcsin{\left(\pm\sqrt{\left(h_1^2+h_2^2\right)}\right)} θ5=arcsin(±(h12+h22))
就能求出 θ 5 \theta_5 θ5但是根据前面的说法,最好用atan2()函数来求解,所以这里的结果只用来判断 θ 5 \theta_5 θ5是不是趋向于0
根据程序验证,当 θ 5 \theta_5 θ5取值为0时,由于电脑的舍入误差的影响,经过计算的 θ 5 \theta_5 θ5的数值并不为0,而是一个极小的值。
如果直接判断 θ 5 \theta_5 θ5是否为零,则不但会使判断失效,还会影响 θ 4 \theta_4 θ4的取值,因此这里虽然写作判断 θ 5 \theta_5 θ5是否为0,但在程序中是判断 s 5 2 s_5^2 s52的是否小于某一特定值。
当
θ
5
≠
0
\theta_5\neq0
θ5=0时
θ
4
=
A
t
a
n
2
(
h
2
,
h
1
)
\theta_4=\mathrm{Atan}2\left(h_2,h_1\right)
θ4=Atan2(h2,h1)
当
θ
5
=
0
\theta_5=0
θ5=0时,机械臂处于奇异位形,关节4和关节6重合成一条直线,此时所有解都是
θ
4
\theta_4
θ4与
θ
6
\theta_6
θ6的和或差。在这种情况下
θ
4
\theta_4
θ4可以任意取值,但一般选择保持其当前值。
- matlab代码实现
%% theta4求解
h1=ax*cos(theta1)*cos(theta2+theta3)+ay*sin(theta1)*cos(theta2+theta3)+az*sin(theta2+theta3);
h2=ax*sin(theta1)-ay*cos(theta1);
s5sq=h1^2+h2^2; % 用sin(theta5)的平方作为判断机械臂是否处于奇异位形
% 需要判断theta5是否为0
% 这里判断theta5是否为0其实有点问题,因为当theta5接近0的时候就会出问题,所以这里选择判断sin(theta5)的平方是否小于某一特定值,若小于则认为theta5为0
% 当theta5=0时,theta4保持不变
% 当theta5≠0时,根据theta4可能取到两组值
if s5sq<0.0000001
theta4=q_r(4); %q_r(4)是上一步theta4的值
else
theta4_1=atan2(h2,h1);
theta4_2=atan2(-h2,-h1);
end
○ 求解 θ 5 \theta_5 θ5
将末端位姿描述矩阵写成
4
3
T
−
1
3
2
T
−
1
2
1
T
−
1
1
0
T
−
1
6
0
T
=
6
5
T
(
θ
6
)
5
4
T
(
θ
6
)
\ \ {{_4^3}T}^{-1}\ {{_3^2}T}^{-1}\ {{_2^1}T}^{-1}\ {{_1^0}T}^{-1}\ _6^0T=_6^5T\left(\theta_6\right)\ {_5^4}T\left(\theta_6\right)
43T−1 32T−1 21T−1 10T−1 60T=65T(θ6) 54T(θ6)
则
4
3
T
−
1
3
2
T
−
1
2
1
T
−
1
1
0
T
−
1
=
[
s
1
s
4
+
c
1
c
4
c
23
s
1
c
4
c
23
−
c
1
s
4
c
4
s
23
−
a
1
c
4
c
23
−
a
2
c
3
c
4
−
a
3
c
4
−
d
1
c
4
s
23
s
1
c
4
−
c
1
s
4
c
23
−
s
1
s
4
c
23
−
c
1
c
4
−
s
4
s
23
a
1
s
4
c
23
+
a
2
c
3
c
4
+
a
3
s
4
+
d
1
s
4
s
23
c
1
s
23
s
1
s
23
−
c
23
−
a
1
s
23
−
a
2
s
3
+
d
1
c
23
−
d
4
0
0
0
1
]
\ {{_4^3}T}^{-1}\ {{_3^2}T}^{-1}\ {{_2^1}T}^{-1}\ {{_1^0}T}^{-1}=\\\left[\begin{matrix}s_1s_4+c_1c_4c_{23}&s_1c_4c_{23}-c_1s_4&c_4s_{23}&-a_1c_4c_{23}-a_2c_3c_4-a_3c_4-d_1c_4s_{23}\\s_1c_4-c_1s_4c_{23}&-s_1s_4c_{23}-c_1c_4&-s_4s_{23}&a_1s_4c_{23}+a_2c_3c_4+a_3s_4+d_1s_4s_{23}\\c_1s_{23}&s_1s_{23}&-c_{23}&-a_1s_{23}-a_2s_3+d_1c_{23}-d_4\\0&0&0&1\\\end{matrix}\right]
43T−1 32T−1 21T−1 10T−1=
s1s4+c1c4c23s1c4−c1s4c23c1s230s1c4c23−c1s4−s1s4c23−c1c4s1s230c4s23−s4s23−c230−a1c4c23−a2c3c4−a3c4−d1c4s23a1s4c23+a2c3c4+a3s4+d1s4s23−a1s23−a2s3+d1c23−d41
5
4
T
(
θ
5
)
6
5
T
(
θ
6
)
=
[
c
5
c
6
−
c
5
s
6
s
5
0
s
6
c
6
0
0
−
s
5
c
6
s
5
s
6
c
5
0
0
0
0
1
]
{_5^4}T\left(\theta_5\right)\ {_6^5}T\left(\theta_6\right)=\left[\begin{matrix}c_5c_6&-c_5s_6&s_5&0\\s_6&c_6&0&0\\-s_5c_6&s_5s_6&c_5&0\\0&0&0&1\\\end{matrix}\right]
54T(θ5) 65T(θ6)=
c5c6s6−s5c60−c5s6c6s5s60s50c500001
- 计算过程参考 θ 4 \theta_4 θ4的过程
结果如下
T_04_inv =
[
sin(Q1)*sin(Q4) + cos(Q1)*cos(Q2)*cos(Q3)*cos(Q4) - cos(Q1)*cos(Q4)*sin(Q2)*sin(Q3),
cos(Q2)*cos(Q3)*cos(Q4)*sin(Q1) - cos(Q1)*sin(Q4) - cos(Q4)*sin(Q1)*sin(Q2)*sin(Q3),
sin(Q2 + Q3)*cos(Q4),
-cos(Q4)*(a3 + a1*cos(Q2 + Q3) + d1*sin(Q2 + Q3) + a2*cos(Q3))
]
[
cos(Q4)*sin(Q1) - cos(Q1)*cos(Q2)*cos(Q3)*sin(Q4) + cos(Q1)*sin(Q2)*sin(Q3)*sin(Q4),
sin(Q1)*sin(Q2)*sin(Q3)*sin(Q4) - cos(Q2)*cos(Q3)*sin(Q1)*sin(Q4) - cos(Q1)*cos(Q4),
-sin(Q2 + Q3)*sin(Q4),
sin(Q4)*(a3 + a1*cos(Q2 + Q3) + d1*sin(Q2 + Q3) + a2*cos(Q3))
]
[
sin(Q2 + Q3)*cos(Q1),
sin(Q2 + Q3)*sin(Q1),
-cos(Q2 + Q3),
d1*cos(Q2 + Q3) - d4 - a1*sin(Q2 + Q3) - a2*sin(Q3)]
[0,0,0,1]
T_left =
[
nx*(sin(Q1)*sin(Q4) + cos(Q1)*cos(Q2)*cos(Q3)*cos(Q4) - cos(Q1)*cos(Q4)*sin(Q2)*sin(Q3)) - ny*(cos(Q1)*sin(Q4) - cos(Q2)*cos(Q3)*cos(Q4)*sin(Q1) + cos(Q4)*sin(Q1)*sin(Q2)*sin(Q3)) + nz*sin(Q2 + Q3)*cos(Q4),
ox*(sin(Q1)*sin(Q4) + cos(Q1)*cos(Q2)*cos(Q3)*cos(Q4) - cos(Q1)*cos(Q4)*sin(Q2)*sin(Q3)) - oy*(cos(Q1)*sin(Q4) - cos(Q2)*cos(Q3)*cos(Q4)*sin(Q1) + cos(Q4)*sin(Q1)*sin(Q2)*sin(Q3)) + oz*sin(Q2 + Q3)*cos(Q4),
ax*(sin(Q1)*sin(Q4) + cos(Q1)*cos(Q2)*cos(Q3)*cos(Q4) - cos(Q1)*cos(Q4)*sin(Q2)*sin(Q3)) - ay*(cos(Q1)*sin(Q4) - cos(Q2)*cos(Q3)*cos(Q4)*sin(Q1) + cos(Q4)*sin(Q1)*sin(Q2)*sin(Q3)) + az*sin(Q2 + Q3)*cos(Q4),
px*(sin(Q1)*sin(Q4) + cos(Q1)*cos(Q2)*cos(Q3)*cos(Q4) - cos(Q1)*cos(Q4)*sin(Q2)*sin(Q3)) - cos(Q4)*(a3 + a1*cos(Q2 + Q3) + d1*sin(Q2 + Q3) + a2*cos(Q3)) - py*(cos(Q1)*sin(Q4) - cos(Q2)*cos(Q3)*cos(Q4)*sin(Q1) + cos(Q4)*sin(Q1)*sin(Q2)*sin(Q3)) + pz*sin(Q2 + Q3)*cos(Q4)
]
[
nx*(cos(Q4)*sin(Q1) - cos(Q1)*cos(Q2)*cos(Q3)*sin(Q4) + cos(Q1)*sin(Q2)*sin(Q3)*sin(Q4)) - ny*(cos(Q1)*cos(Q4) + cos(Q2)*cos(Q3)*sin(Q1)*sin(Q4) - sin(Q1)*sin(Q2)*sin(Q3)*sin(Q4)) - nz*sin(Q2 + Q3)*sin(Q4),
ox*(cos(Q4)*sin(Q1) - cos(Q1)*cos(Q2)*cos(Q3)*sin(Q4) + cos(Q1)*sin(Q2)*sin(Q3)*sin(Q4)) - oy*(cos(Q1)*cos(Q4) + cos(Q2)*cos(Q3)*sin(Q1)*sin(Q4) - sin(Q1)*sin(Q2)*sin(Q3)*sin(Q4)) - oz*sin(Q2 + Q3)*sin(Q4),
ax*(cos(Q4)*sin(Q1) - cos(Q1)*cos(Q2)*cos(Q3)*sin(Q4) + cos(Q1)*sin(Q2)*sin(Q3)*sin(Q4)) - ay*(cos(Q1)*cos(Q4) + cos(Q2)*cos(Q3)*sin(Q1)*sin(Q4) - sin(Q1)*sin(Q2)*sin(Q3)*sin(Q4)) - az*sin(Q2 + Q3)*sin(Q4),
px*(cos(Q4)*sin(Q1) - cos(Q1)*cos(Q2)*cos(Q3)*sin(Q4) + cos(Q1)*sin(Q2)*sin(Q3)*sin(Q4)) + sin(Q4)*(a3 + a1*cos(Q2 + Q3) + d1*sin(Q2 + Q3) + a2*cos(Q3)) - py*(cos(Q1)*cos(Q4) + cos(Q2)*cos(Q3)*sin(Q1)*sin(Q4) - sin(Q1)*sin(Q2)*sin(Q3)*sin(Q4)) - pz*sin(Q2 + Q3)*sin(Q4)
]
[
ny*sin(Q2 + Q3)*sin(Q1) - nz*cos(Q2 + Q3) + nx*sin(Q2 + Q3)*cos(Q1),
oy*sin(Q2 + Q3)*sin(Q1) - oz*cos(Q2 + Q3) + ox*sin(Q2 + Q3)*cos(Q1),
ax*sin(Q2 + Q3)*cos(Q1) - az*cos(Q2 + Q3) + ay*sin(Q2 + Q3)*sin(Q1),
d1*cos(Q2 + Q3) - d4 - pz*cos(Q2 + Q3) - a1*sin(Q2 + Q3) - a2*sin(Q3) + py*sin(Q2 + Q3)*sin(Q1) + px*sin(Q2 + Q3)*cos(Q1)
]
[0,0,0,1]
T_46 =
[ cos(Q5)*cos(Q6), -cos(Q5)*sin(Q6), sin(Q5), 0]
[ sin(Q6), cos(Q6), 0, 0]
[-cos(Q6)*sin(Q5), sin(Q5)*sin(Q6), cos(Q5), 0]
[ 0, 0, 0, 1]
令元素(1,3)和(3,3)等号左右相等得到:
a
x
(
s
1
s
4
+
c
1
c
4
c
23
)
+
a
y
(
s
1
c
4
c
23
−
c
1
s
4
)
+
a
z
(
c
4
s
23
)
=
s
5
a
x
(
c
1
s
23
)
+
a
y
(
s
1
s
23
)
+
a
z
(
−
c
23
)
=
c
5
a_x\left(s_1s_4+c_1c_4c_{23}\right)+a_y\left(s_1c_4c_{23}-c_1s_4\right)+a_z\left(c_4s_{23}\right)=s_5\\ a_x\left(c_1s_{23}\right)+a_y\left(s_1s_{23}\right)+a_z\left(-c_{23}\right)=c_5
ax(s1s4+c1c4c23)+ay(s1c4c23−c1s4)+az(c4s23)=s5ax(c1s23)+ay(s1s23)+az(−c23)=c5
令
p
1
=
a
x
(
s
1
s
4
+
c
1
c
4
c
23
)
+
a
y
(
s
1
c
4
c
23
−
c
1
s
4
)
+
a
z
(
c
4
s
23
)
p
2
=
a
x
(
c
1
s
23
)
+
a
y
(
s
1
s
23
)
+
a
z
(
−
c
23
)
p_1=a_x\left(s_1s_4+c_1c_4c_{23}\right)+a_y\left(s_1c_4c_{23}-c_1s_4\right)+a_z\left(c_4s_{23}\right)\\ p_2=a_x\left(c_1s_{23}\right)+a_y\left(s_1s_{23}\right)+a_z\left(-c_{23}\right)
p1=ax(s1s4+c1c4c23)+ay(s1c4c23−c1s4)+az(c4s23)p2=ax(c1s23)+ay(s1s23)+az(−c23)
则
θ
5
=
A
t
a
n
2
(
p
1
,
p
2
)
\theta_5=\mathrm{Atan}2\left(p_1,p_2\right)
θ5=Atan2(p1,p2)
- matlab代码实现
p1=ax*(sin(theta1)*sin(theta4)+cos(theta1)*cos(theta4)*cos(theta2+theta3))+...
ay*(sin(theta1)*cos(theta4)*cos(theta2+theta3)-cos(theta1)*sin(theta4))+...
az*cos(theta4)*sin(theta2+theta3);
p2=ax*cos(theta1)*sin(theta2+theta3)+ay*sin(theta1)*sin(theta2+theta3)-az*cos(theta2+theta3);
theta5_1=atan2(p1,p2);
theta5_2=atan2(-p1,-p2);
○ 求解 θ 6 \theta_6 θ6
将等式写成
5
4
T
−
1
4
3
T
−
1
3
2
T
−
1
2
1
T
−
1
1
0
T
−
1
6
0
T
=
6
5
T
(
θ
6
)
\ {{_5^4}T}^{-1}\ {{_4^3}T}^{-1}\ {{_3^2}T}^{-1}\ {{_2^1}T}^{-1}\ {{_1^0}T}^{-1}\ _6^0T=_6^5T\left(\theta_6\right)
54T−1 43T−1 32T−1 21T−1 10T−1 60T=65T(θ6)
记
5
4
T
−
1
4
3
T
−
1
3
2
T
−
1
2
1
T
−
1
1
0
T
−
1
=
[
m
11
m
12
m
13
m
14
m
21
m
22
m
23
m
24
m
31
m
32
m
33
m
34
0
0
0
1
]
\ {{_5^4}T}^{-1}\ {{_4^3}T}^{-1}\ {{_3^2}T}^{-1}\ {{_2^1}T}^{-1}\ {{_1^0}T}^{-1}=\left[\begin{matrix}m_{11}&m_{12}&m_{13}&m_{14}\\m_{21}&m_{22}&m_{23}&m_{24}\\m_{31}&m_{32}&m_{33}&m_{34}\\0&0&0&1\\\end{matrix}\right]
54T−1 43T−1 32T−1 21T−1 10T−1=
m11m21m310m12m22m320m13m23m330m14m24m341
其中
m 11 = s 1 s 4 c 5 − c 1 s 5 s 23 + c 1 c 4 c 5 c 23 m 12 = − c 1 s 4 c 5 − s 1 s 5 s 23 + s 1 c 4 c 5 c 23 m 13 = s 5 c 23 + c 4 c 5 s 23 m 31 = s 1 c 4 − c 1 s 4 c 23 m 32 = − c 1 c 4 − s 1 s 4 c 23 m 33 = − s 4 s 23 \begin{aligned} m_{11}&=s_1s_4c_5-c_1s_5s_{23}+c_1c_4c_5c_{23}\\ m_{12}&=-c_1s_4c_5-s_1s_5s_{23}+s_1c_4c_5c_{23}\\ m_{13}&=s_5c_{23}+c_4c_5s_{23}\\ m_{31}&=s_1c_4-c_1s_4c_{23}\\ m_{32}&=-c_1c_4-s_1s_4c_{23}\\ m_{33}&=-s_4s_{23}\\ \end{aligned} m11m12m13m31m32m33=s1s4c5−c1s5s23+c1c4c5c23=−c1s4c5−s1s5s23+s1c4c5c23=s5c23+c4c5s23=s1c4−c1s4c23=−c1c4−s1s4c23=−s4s23
- 计算过程参考 θ 4 \theta_4 θ4的过程
结果如下
T_05_inv =
[
cos(Q5)*sin(Q1)*sin(Q4) - cos(Q1)*cos(Q2)*sin(Q3)*sin(Q5) - cos(Q1)*cos(Q3)*sin(Q2)*sin(Q5) - cos(Q1)*cos(Q4)*cos(Q5)*sin(Q2)*sin(Q3) + cos(Q1)*cos(Q2)*cos(Q3)*cos(Q4)*cos(Q5),
%=c5s1s4-c1c2s3s5-c1c3s2s5-c1c4c5s2s3+c1c2c3c4c5
%=c5s1s4-c1s5(c2s3+s2c3)+c1c4c5(c2c3-s2s3)
%=c5s1s4-c1s5s23+c1c4c5c23
cos(Q2)*cos(Q3)*cos(Q4)*cos(Q5)*sin(Q1) - cos(Q2)*sin(Q1)*sin(Q3)*sin(Q5) - cos(Q3)*sin(Q1)*sin(Q2)*sin(Q5) - cos(Q4)*cos(Q5)*sin(Q1)*sin(Q2)*sin(Q3) - cos(Q1)*cos(Q5)*sin(Q4),
%=c2c3c4c5s1-c2s1s3s5-c3s1s2s5-c4c5s1s2s3-c1c5s4
%=s1c4c5(c2c3-s2s3)-s1s5(s2c3+c2s3)-c1c5s4
%=s1c4c5c23-s1s5s23-c1c5s4
cos(Q2)*cos(Q3)*sin(Q5) - sin(Q2)*sin(Q3)*sin(Q5) + cos(Q2)*cos(Q4)*cos(Q5)*sin(Q3) + cos(Q3)*cos(Q4)*cos(Q5)*sin(Q2),
%=c2c3s5-s2s3s5+c2c4c5s3+c3c4c5s2
%=s5(c2c3-s2s3)+c4c5(c2s3+s2c3)
%=s5c23+c4c5s23
d4*sin(Q5) - a3*cos(Q4)*cos(Q5) + a2*sin(Q3)*sin(Q5) + d1*sin(Q2)*sin(Q3)*sin(Q5) - a2*cos(Q3)*cos(Q4)*cos(Q5) - d1*cos(Q2)*cos(Q3)*sin(Q5) + a1*cos(Q2)*sin(Q3)*sin(Q5) + a1*cos(Q3)*sin(Q2)*sin(Q5) - a1*cos(Q2)*cos(Q3)*cos(Q4)*cos(Q5) - d1*cos(Q2)*cos(Q4)*cos(Q5)*sin(Q3) - d1*cos(Q3)*cos(Q4)*cos(Q5)*sin(Q2) + a1*cos(Q4)*cos(Q5)*sin(Q2)*sin(Q3)
]
[
cos(Q1)*cos(Q4)*sin(Q2)*sin(Q3)*sin(Q5) - cos(Q1)*cos(Q2)*cos(Q5)*sin(Q3) - cos(Q1)*cos(Q3)*cos(Q5)*sin(Q2) - sin(Q1)*sin(Q4)*sin(Q5) - cos(Q1)*cos(Q2)*cos(Q3)*cos(Q4)*sin(Q5),
cos(Q1)*sin(Q4)*sin(Q5) - cos(Q2)*cos(Q5)*sin(Q1)*sin(Q3) - cos(Q3)*cos(Q5)*sin(Q1)*sin(Q2) - cos(Q2)*cos(Q3)*cos(Q4)*sin(Q1)*sin(Q5) + cos(Q4)*sin(Q1)*sin(Q2)*sin(Q3)*sin(Q5),
cos(Q2)*cos(Q3)*cos(Q5) - cos(Q5)*sin(Q2)*sin(Q3) - cos(Q2)*cos(Q4)*sin(Q3)*sin(Q5) - cos(Q3)*cos(Q4)*sin(Q2)*sin(Q5),
d4*cos(Q5) + a2*cos(Q5)*sin(Q3) + a3*cos(Q4)*sin(Q5) + d1*cos(Q5)*sin(Q2)*sin(Q3) - d1*cos(Q2)*cos(Q3)*cos(Q5) + a1*cos(Q2)*cos(Q5)*sin(Q3) + a1*cos(Q3)*cos(Q5)*sin(Q2) + a2*cos(Q3)*cos(Q4)*sin(Q5) + a1*cos(Q2)*cos(Q3)*cos(Q4)*sin(Q5) + d1*cos(Q2)*cos(Q4)*sin(Q3)*sin(Q5) + d1*cos(Q3)*cos(Q4)*sin(Q2)*sin(Q5) - a1*cos(Q4)*sin(Q2)*sin(Q3)*sin(Q5)
]
[
cos(Q4)*sin(Q1) - cos(Q1)*cos(Q2)*cos(Q3)*sin(Q4) + cos(Q1)*sin(Q2)*sin(Q3)*sin(Q4),
%=c4s1-c1c2c3s4+c1s2s3s4
%=s1c4-c1s4(c2c3-s2s3)
sin(Q1)*sin(Q2)*sin(Q3)*sin(Q4) - cos(Q2)*cos(Q3)*sin(Q1)*sin(Q4) - cos(Q1)*cos(Q4),
%=s1s2s3s4-c2c3s1s4-c1c4
%=-c1c4-s1s4c23
-sin(Q2 + Q3)*sin(Q4),
sin(Q4)*(a3 + a1*cos(Q2 + Q3) + d1*sin(Q2 + Q3) + a2*cos(Q3))
]
[0,0,0,1]
将以上结果带入()中,通过观察等式两边的矩阵,令元素(1,1)和(3,1)等号左右相等得到:
n x m 11 + n y m 12 + n z m 13 = c 6 n x m 31 + n y m 32 + n z m 33 = s 6 n_xm_{11}+n_ym_{12}+n_zm_{13}=c_6 n_xm_{31}+n_ym_{32}+n_zm_{33}=s_6 nxm11+nym12+nzm13=c6nxm31+nym32+nzm33=s6
这里就不放过程了
解得
θ 6 = A t a n 2 ( n x m 31 + n y m 32 + n z m 33 , n x m 11 + n y m 12 + n z m 13 ) \theta_6=\mathrm{Atan}2\left(n_xm_{31}+n_ym_{32}+n_zm_{33},n_xm_{11}+n_ym_{12}+n_zm_{13}\right) θ6=Atan2(nxm31+nym32+nzm33,nxm11+nym12+nzm13)
- matlab代码实现
%% theta6求解
m11=sin(theta1)*sin(theta4)*cos(theta5)-cos(theta1)*sin(theta5)*sin(theta2+theta3)+cos(theta1)*cos(theta4)*cos(theta5)*cos(theta2+theta3);
m12=-cos(theta1)*sin(theta4)*cos(theta5)-sin(theta1)*sin(theta5)*sin(theta2+theta3)+sin(theta1)*cos(theta4)*cos(theta5)*cos(theta2+theta3);
m13=sin(theta5)*cos(theta2+theta3)+cos(theta4)*cos(theta5)*sin(theta2+theta3);
m31=sin(theta1)*cos(theta4)-cos(theta1)*sin(theta4)*cos(theta2+theta3);
m32=-cos(theta1)*cos(theta4)-sin(theta1)*sin(theta4)*cos(theta2+theta3);
m33=-sin(theta4)*sin(theta2+theta3);
theta6_1=atan2(nx*m31+ny*m32+nz*m33,nx*m11+ny*m12+nz*m13);
theta6_2=atan2(-(nx*m31+ny*m32+nz*m33),-(nx*m11+ny*m12+nz*m13));