翻译：

 

D. 点

时间限制：3秒

内存限制：256兆字节

输入：标准输入

输出：标准输出

Anton和Dasha喜欢在棋盘纸上玩不同的游戏。到11年级时，他们成功玩过了所有这类游戏，并请程序员Vova想出一个新的游戏。Vova建议他们玩一个名为“点”的游戏，规则如下：

在棋盘纸上绘制一个坐标系。一个点最初放在位置(x, y)上。
移动是将一个点移动到预选向量中的一个。每个玩家还可以每局游戏对点相对于直线y = x进行对称反射一次。
Anton和Dasha轮流进行。Anton先行动。
如果在某个玩家的回合中，点到坐标原点的距离超过d，则该玩家输掉游戏。
帮助他们确定赢家。

输入

输入文件的第一行包含4个整数x，y，n，d（-200 ≤ x，y ≤ 200，1 ≤ d ≤ 200，1 ≤ n ≤ 20）-点的初始坐标，距离d和向量的数量。保证初始点距离坐标原点的距离小于d。接下来的n行每行包含两个非负整数xi和yi（0 ≤ xi，yi ≤ 200）-第i个向量的坐标。保证所有向量均为非零且不同。

输出

如果在两个玩家都按最佳方式进行游戏的情况下，获胜者是Anton，则输出“Anton”，否则输出“Dasha”。

示例

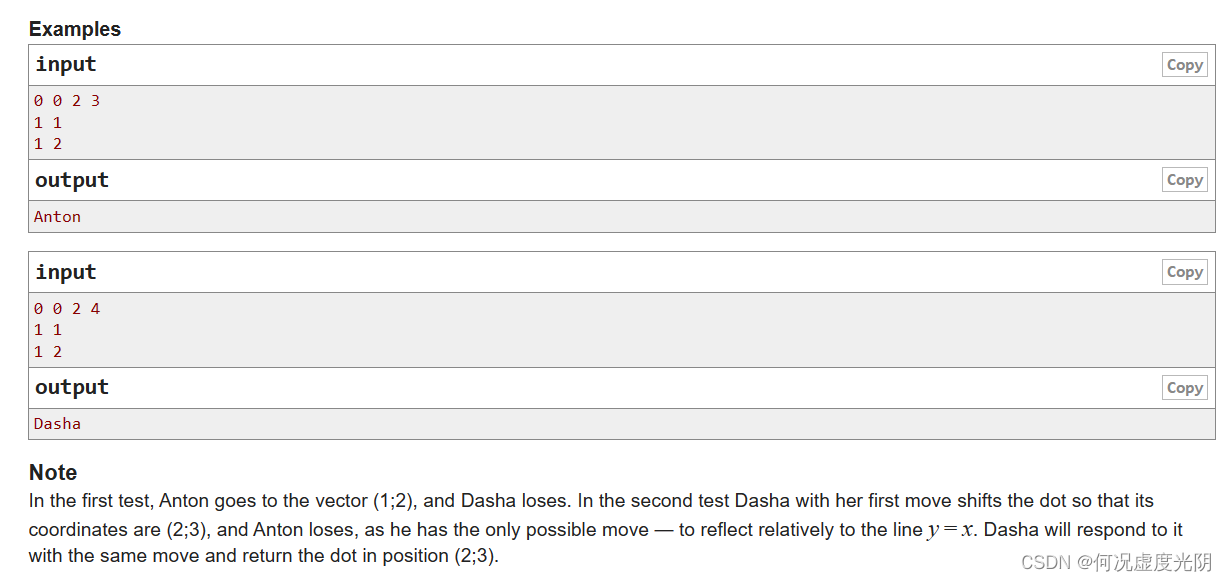
输入
0 0 2 3
1 1
1 2
输出
Anton

输入
0 0 2 4
1 1
1 2
输出
Dasha

注意
在第一个测试中，Anton选择向量（1, 2），Dasha输掉游戏。在第二个测试中，Dasha在她的第一次移动中将点移动到坐标（2, 3），Anton输掉游戏，因为他只有一种可能的移动方式-相对于直线y = x进行反射。Dasha将以相同的方式回应，并将点返回到位置（2, 3）。

思路：

这个问题可以通过模拟游戏的过程来解决。我们可以使用两个变量来追踪点的当前坐标，然后根据规则进行移动和反射操作。在每个玩家的回合，我们都会选择使得点移动到离原点更远的位置。首先我们进入游戏的循环，交替进行Anton和Dasha的回合，直到有一个玩家输掉游戏。在每个回合中，我们根据当前点的坐标和可用的向量，选择一个使得点移动到离原点更远的位置。如果没有可行的移动操作，即点已经超出了距离限制d，则当前玩家输掉游戏。除了移动操作之外，每个玩家还可以选择对点进行一次反射操作。反射操作将点的坐标相对于直线y = x进行对称反射。我们可以通过交换点的x坐标和y坐标来实现这个反射。最后，我们根据游戏的结果输出Anton或Dasha作为获胜者。

解法：

首先我们可以发现题目中的点可以移动到y=x的对称点这条件没用，因为一个人使用了这个条件，另一个人也可以使用它使点回到刚刚的位置。然后问题就转化为 给个初始点，然后两个人轮流移动一段距离，当点和原点的距离大于d时失败。记忆化搜索就行了。

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
const int INF=2e18;
int d,n;
struct node{
	int x,y; 
}a[N];
int f[500][500];
int get_dist(int a,int b){
	return (a-200)*(a-200)+(b-200)*(b-200)<=d*d;
}
int dfs(int x,int y){
	int xx,yy;
	if(f[x][y]) return f[x][y];
	for(int i=1;i<=n;i++){
		xx=x+a[i].x;
		yy=y+a[i].y;
		if(get_dist(xx,yy)){
			if(dfs(xx,yy)==2){
				return f[x][y]=1;
			}
		}
	}
	return f[x][y]=2;
}
void solve(){
	int x,y;
	cin>>x>>y>>n>>d;
	for(int i=1;i<=n;i++){
		cin>>a[i].x>>a[i].y;
	}
	if(dfs(x+200,y+200)==1) cout<<"Anton\n";
	else cout<<"Dasha\n";
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0); 
	int t=1;
	while(t--){
		solve();
	}
}