一、前言
此示例使用无限数组分析对大型有限数组进行建模。晶胞上的无限阵列分析揭示了特定频率下的扫描阻抗行为。此信息与隔离元件图案和阻抗的知识一起使用,以计算扫描元件图案。然后,使用数组中的每个元素都具有相同扫描元素模式的假设对大型有限数组进行建模。此示例需要天线工具箱。
二、定义单个元素
在本例中,我们选择X波段的中心作为设计频率。创建一个长度略小于的薄偶极子
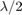
并将其作为激励器分配给无限大的反射器。
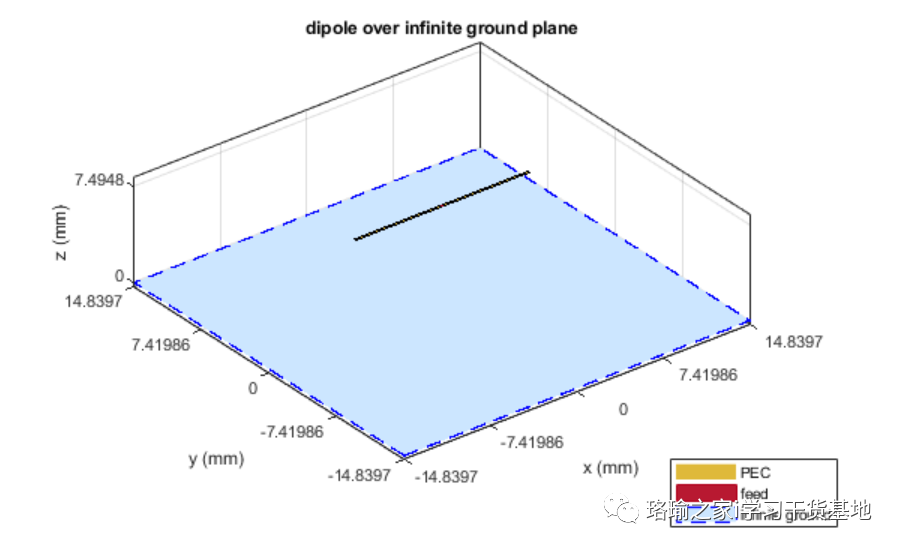
计算上述天线的隔离元件方向图和阻抗。这些结果将用于计算扫描元件图案(SEP)。该术语也称为数组元素模式 (AEP) 或嵌入式元素模式 (EEP)。
三、计算无限阵列扫描元素模式
晶胞在无限数组分析中,术语晶胞是指无限数组中的单个元素。单元元件需要接地层。没有接地层的天线需要由反射器支撑。每种情况的代表性示例是由反射器和微带贴片天线支持的偶极子。本例将使用由反射器支撑的偶极子,并分析10 GHz下的阻抗行为作为扫描角度的函数。晶胞将具有一个
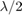
x
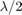
横截面。
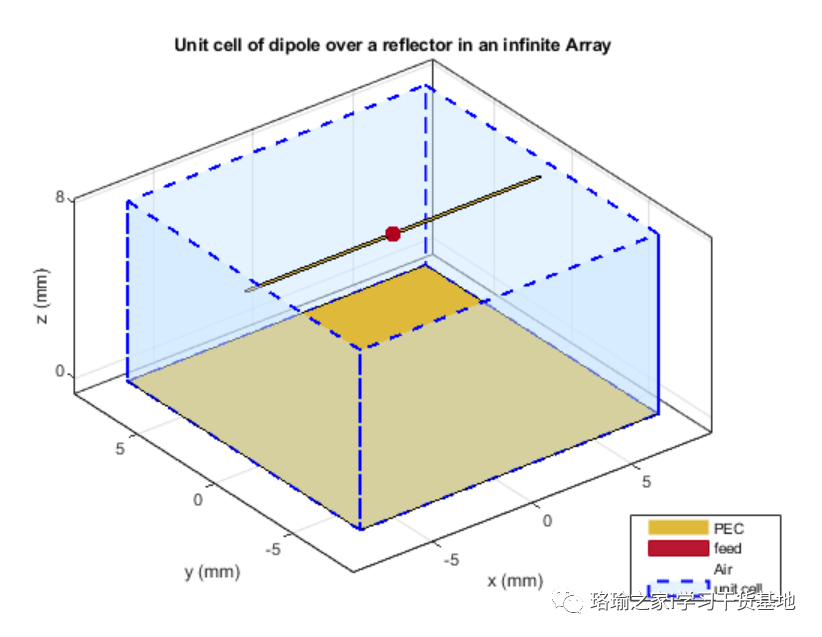
扫描阻抗单频和单扫描角度下的扫描阻抗如下所示。
在本例中,使用周期性格林函数的双重求和中的 50 项计算整个扫描体积的扫描阻抗,以改善收敛行为。
扫描元素图案/阵列元素图案/嵌入式元素图案扫描元件模式(SEP)由无限阵列扫描阻抗、隔离元件模式和隔离元件阻抗计算得出。使用的表达式如下所示[1],[2]:
四、构建自定义天线元素
表示功率模式的扫描元件图案用于构建自定义天线元件。
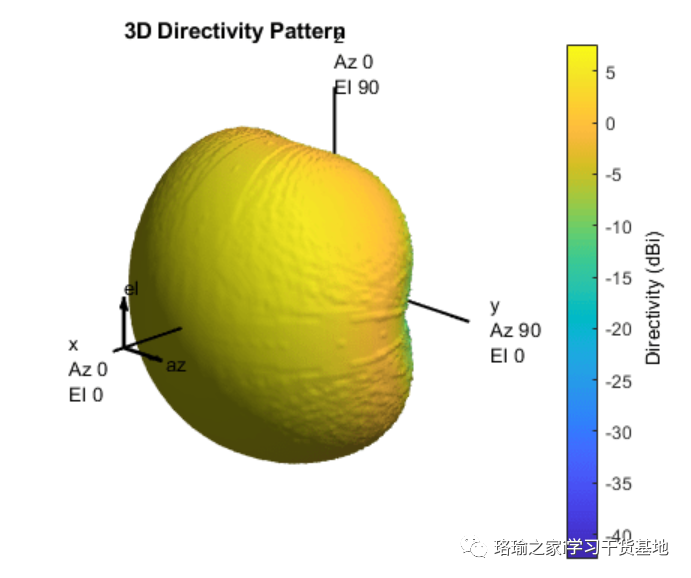
五、构建 21 X 21 URA
使用具有扫描元素模式的自定义天线元素创建统一的矩形阵列 (URA)。
六、在 E 平面和 H 平面中绘制切片
计算使用无限阵列分析构建的阵列的高程平面(由方位角 = 0 度指定,也称为 E 平面)和方位平面(由仰角 = 0 度指定,称为 H 平面)中的模式。

七、与全波有限阵列分析的比较
为了理解阵列有限尺寸的影响,我们对由无限反射器支持的21 X 21偶极子阵列进行了全波分析。还计算了 E 和 H 平面中的全波阵列图案切片以及中心元素嵌入的元素图案。此数据是从 MAT 文件加载的。在具有 630 GB 内存的 2.4 GHz 计算机上,此分析大约需要 32 秒。
加载全波数据并构建自定义天线加载有限阵列分析数据,并使用嵌入式单元模式构建自定义天线单元。请注意,来自全波分析的模式需要旋转 90 度,以便与在 YZ 平面上构建的 URA 模型对齐。
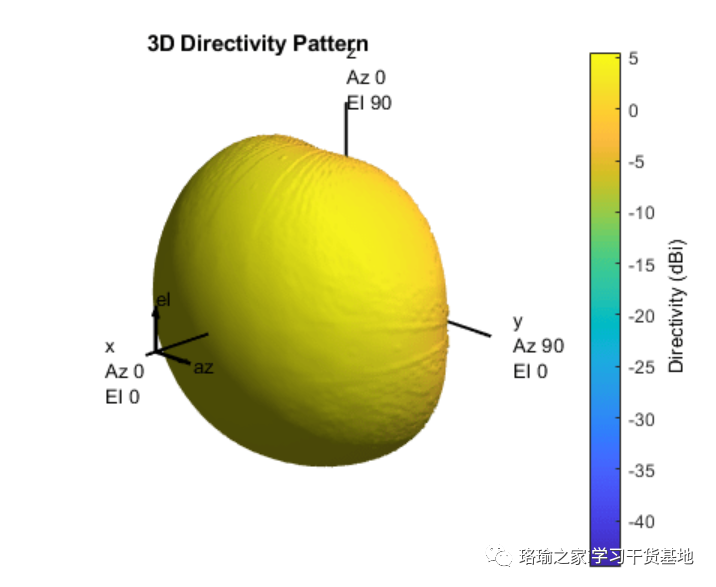
创建具有嵌入式元素模式的统一矩形数组如前所述,使用自定义天线元件创建一个统一的矩形阵列。
E 和 H 平面切片 - 具有嵌入式元素图案的阵列计算具有嵌入元素图案和嵌入元素图案本身的数组的两个正交平面 - E 和 H 中的图案切片。此外,由于数组模式的完整波数据也可用,因此使用它来比较结果。
E 和 H 平面切片 - 来自有限数组的嵌入式元素模式;E 和 H 平面切片 - 有限阵列的全波分析;数组模式的比较此处绘制了两个正交平面中的阵列模式。
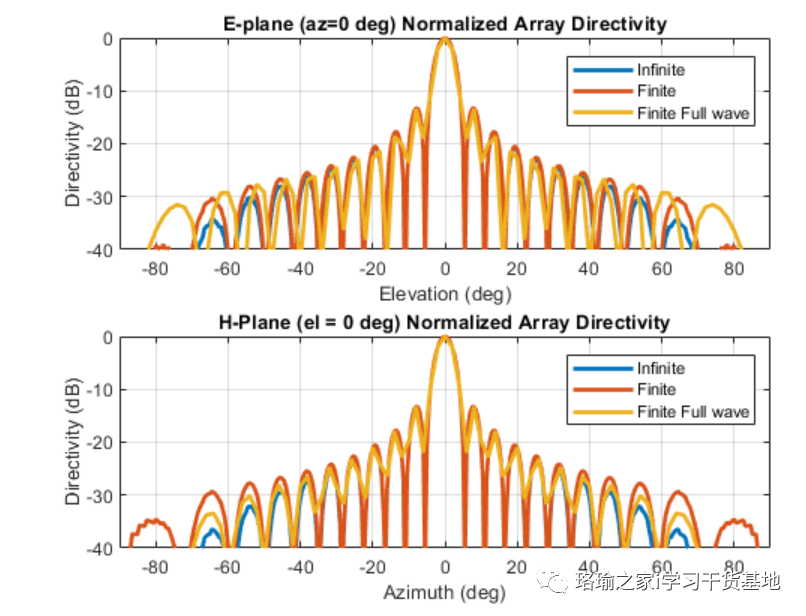
两个平面上的模式图显示,所有三种分析方法都表明,在距视线+/-40度时,行为相似。超出此范围,与有限阵列的全波分析相比,对URA中的所有元素使用扫描元件模式似乎低估了旁瓣水平。造成这种情况的一个可能原因可能是有限大小数组的边缘效应。
元素模式的比较这里比较了无限数组分析和有限数组分析的元素模式。
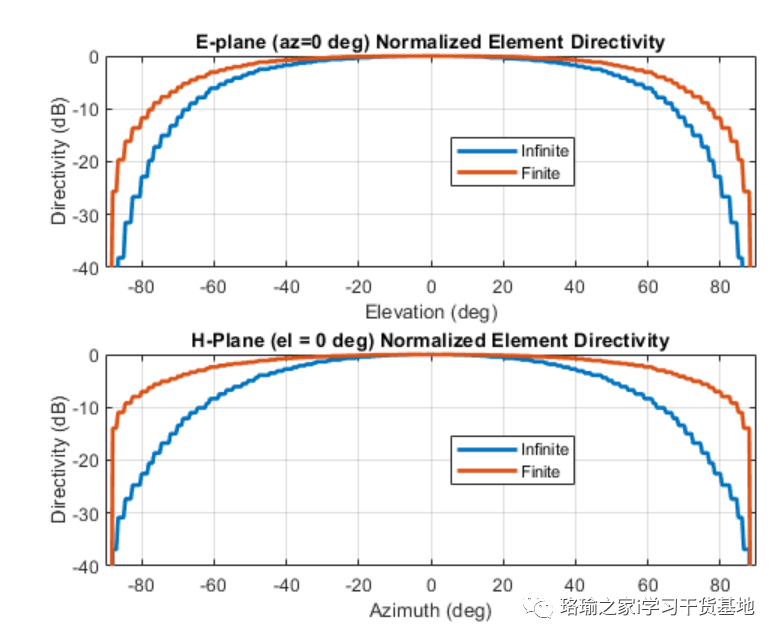
八、使用无限阵列扫描元素模式的扫描行为
根据方位角 = 0 度定义的高程平面中的无限阵列扫描元素图案扫描阵列,并绘制归一化方向性。此外,覆盖规范化扫描元素模式。
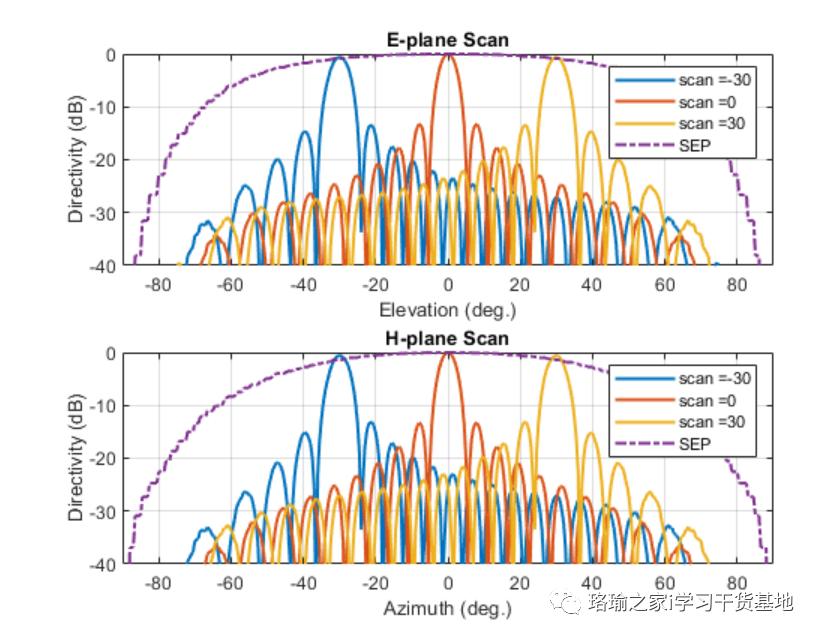
请注意,归一化阵列模式的整体形状大致遵循归一化扫描元素模式。这也可以通过模式乘法原理来预测。
九、结论
无限阵列分析是用于分析和设计大型有限数组的工具之一。分析假设所有元素都相同,边缘效应可以忽略并具有均匀的激励幅度 孤立的元素图案被替换为包含互耦效应的扫描元件图案。
十、程序
使用Matlab R2022b版本,点击打开。(版本过低,运行该程序可能会报错)
程序下载方式一: 基于matlab使用无限阵列分析对大型阵列中的互耦进行建模资源-CSDN文库
程序下载方式二:基于matlab使用无限阵列分析对大型阵列中的互耦进行建模