目录

题目描述

输入描述

输出描述

用例

题目解析

算法源码

---

题目描述

给一块n*m的地块，相当于n*m的二维数组，每个元素的值表示这个小地块的发电量；

求在这块地上建立正方形的边长为c的发电站，发电量满足目标电量k的地块数量。

输入描述

第一行为四个按空格分隔的正整数，分别表示n, m , c k

后面n行整数，表示每个地块的发电量

输出描述

输出满足条件的地块数量

用例

输入	2 5 2 6 1 3 4 5 8 2 3 6 7 1
输出	4
说明	无

题目解析

本题最直观地解法，请看下面代码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
let n, m, c, k;
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 1) {
    [n, m, c, k] = lines[0].split(" ").map(Number);
  }

  if (n && lines.length === n + 1) {
    const matrix = lines.slice(1).map((line) => line.split(" ").map(Number));

    console.log(getResult(matrix, n, m, c, k));

    lines.length = 0;
  }
});

function getResult(matrix, n, m, c, k) {
  let count = 0;

  if (n < c || m < c) return count;

  for (let i = 0; i <= n - c; i++) {
    for (let j = 0; j <= m - c; j++) {
      if (getSum(matrix, i, j, c) >= k) {
        count++;
      }
    }
  }

  return count;
}

function getSum(matrix, row, col, c) {
  let sum = 0;
  for (let i = row; i < row + c; i++) {
    for (let j = col; j < col + c; j++) {
      sum += matrix[i][j];
    }
  }
  return sum;
}

但是这种解法中，存在了大量地重复计算，比如

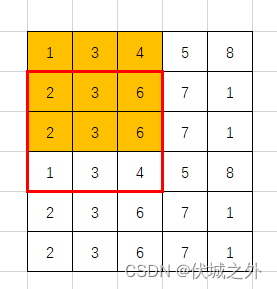
上面图示矩阵，如果从橙色正方形位置，下移一行，变动到红框正方形位置，按照上面逻辑需要对红框正方形中元素重新求和。

但是实际上，我们只需要基于橙色正方形（已经计算过和）减去 失去的一行，加上新增的一行即可。

可能这么看，计算量并没有节省多少，但是一旦正方形很大，则节省的计算量还是非常可观的。

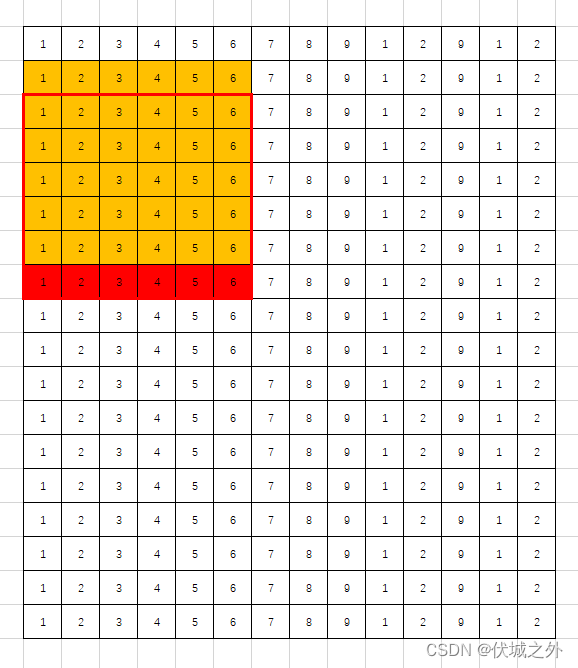
 并且我们还可以将“新增的行”计算得到的和缓存起来，因为如果数据量足够大，“新增的行”也会有变成“失去的行”的时候

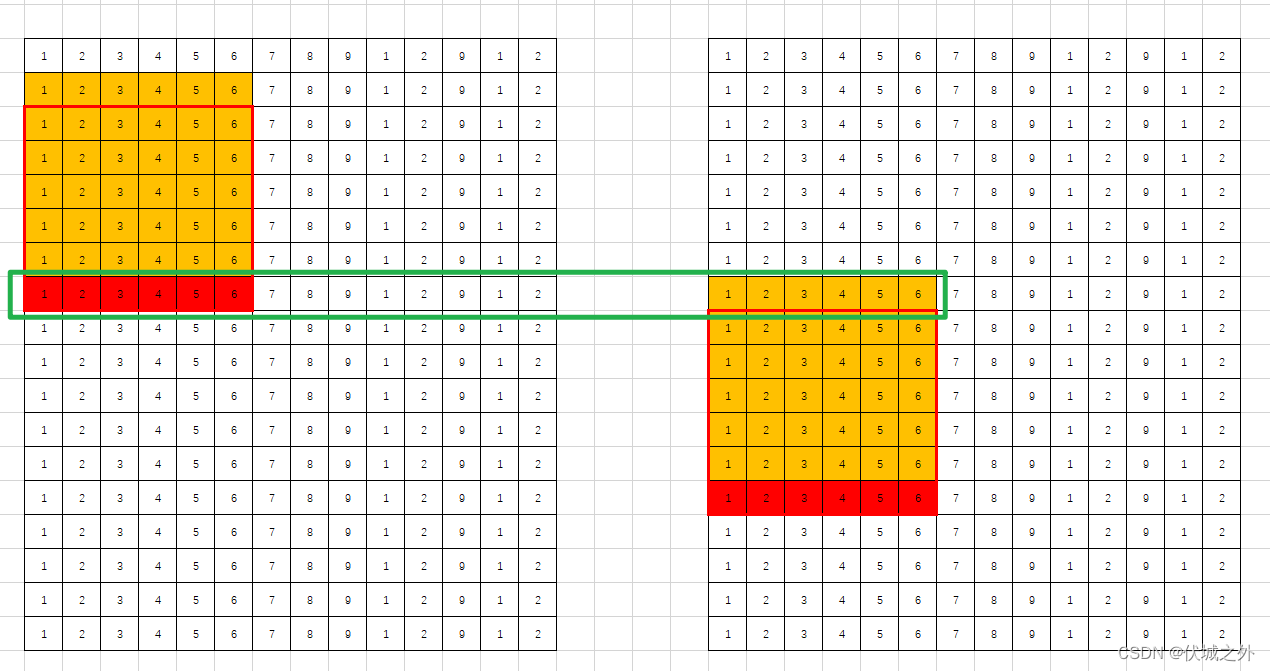
这样又可以节省一些计算量 。

算法源码

/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");

const rl = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});

const lines = [];
let n, m, c, k;
rl.on("line", (line) => {
  lines.push(line);

  if (lines.length === 1) {
    [n, m, c, k] = lines[0].split(" ").map(Number);
  }

  if (n && lines.length === n + 1) {
    const matrix = lines.slice(1).map((line) => line.split(" ").map(Number));

    console.log(getResult(matrix, n, m, c, k));

    lines.length = 0;
  }
});

function getResult(matrix, n, m, c, k) {
  let count = 0;

  if (n < c || m < c) return count;

  let sum = 0;
  for (let i = 0; i < c; i++) {
    for (let j = 0; j < c; j++) {
      sum += matrix[i][j];
    }
  }

  const rows = {};
  function zipR(row) {
    return rows[row]
      ? rows[row]
      : (rows[row] = matrix
          .slice(row, row + 1)
          .slice(0, c)
          .reduce((p, c) => p + c));
  }

  const cols = {};
  function zipC(row, col) {
    const key = `${row}-${col}`;

    return cols[key]
      ? cols[key]
      : (cols[key] = matrix
          .slice(row, row + c)
          .reduce((p, c) => p[col] + c[col]));
  }

  const dp = new Array(n - c + 1)
    .fill(0)
    .map(() => new Array(m - c + 1).fill(0));
  dp[0][0] = sum;

  if (dp[0][0] >= k) count++;

  let i = 0,
    j = 0;
  for (; i <= n - c; i++) {
    if (i !== 0) {
      dp[i][j] = dp[i - 1][j] - zipR(i - 1) + zipR(i + c - 1);
      if (dp[i][j] >= k) count++;
    }

    for (; j <= m - c; j++) {
      if (i === 0 && j === 0) continue;
      dp[i][j] = dp[i][j - 1] - zipC(i, j - 1) + zipC(i, j + c - 1);
      if (dp[i][j] >= k) count++;
    }
  }

  return count;
}