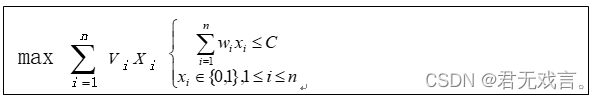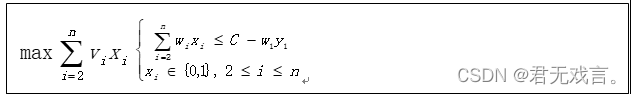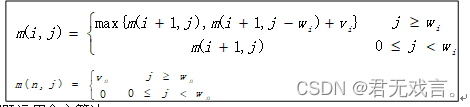| 一、实验目的: 理解并掌握利用-动态规划算法与贪心算法求解不同背包问题。 | |||||||||
给定n种物品和一个背包。物品i的重量是w[i],其价值为vi,背包的容量为C。问如何选择装入背包的物品,使得装入背包中物品的总价值最大? 在选择装入背包的物品时,对每种物品i只有两种选择,即装入背包或不装入背包。不能将物品装入背包多次,也不能只装入部分的物品,因此称之为0-1背包问题。 2. 小数背包问题 给定n种物品和一个背包。物品i的重量是w[i],其价值为vi,背包的容量为C。问如何选择装入背包的物品,使得装入背包中物品的总价值最大? 在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包。 程序代码:
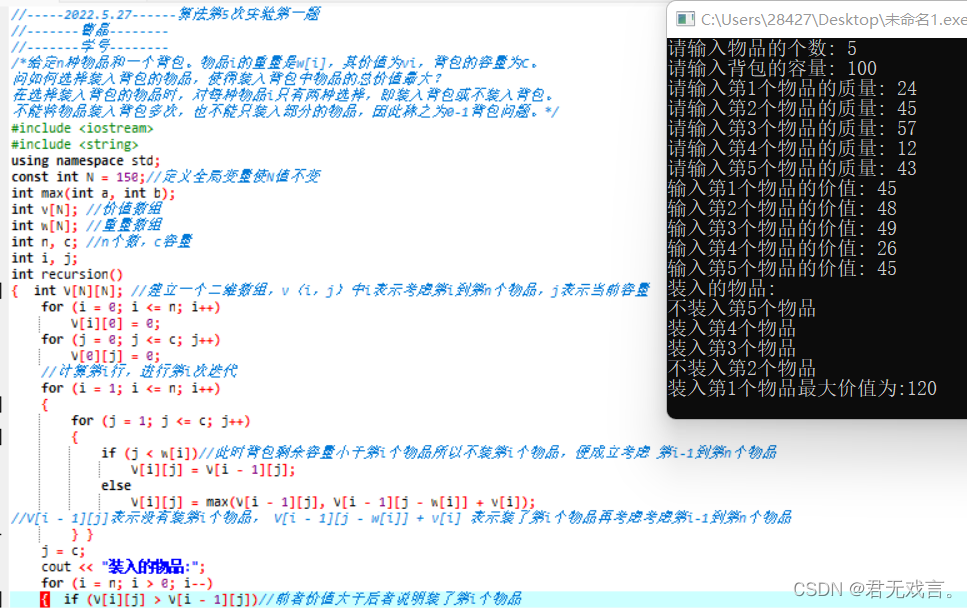
#include <iostream> #include <string> using namespace std; const int N = 150;//定义全局变量使N值不变 int max(int a, int b); int v[N]; //价值数组 int w[N]; //重量数组 int n, c; //n个数,c容量 int i, j; int recursion() { int V[N][N]; //建立一个二维数组,v(i,j)中i表示考虑第i到第n个物品,j表示当前容量 for (i = 0; i <= n; i++) V[i][0] = 0; for (j = 0; j <= c; j++) V[0][j] = 0; //计算第i行,进行第i次迭代 for (i = 1; i <= n; i++) { for (j = 1; j <= c; j++) { if (j < w[i])//此时背包剩余容量小于第i个物品所以不装第i个物品,便成立考虑 第i-1到第n个物品 V[i][j] = V[i - 1][j]; else V[i][j] = max(V[i - 1][j], V[i - 1][j - w[i]] + v[i]); //V[i - 1][j]表示没有装第i个物品, V[i - 1][j - w[i]] + v[i] 表示装了第i个物品再考虑考虑第i-1到第n个物品 } } j = c; cout << "装入的物品:"; for (i = n; i > 0; i--) { if (V[i][j] > V[i - 1][j])//前者价值大于后者说明装了第i个物品 { cout << "\n"; cout << "装入第" << i << "个物品"; j = j - w[i]; continue; } else cout << "\n"; cout << "不装入第" << i << "个物品"; } return V[n][c]; } int max(int a, int b) { if (a >= b) return a; else return b; } int input() { cout << "请输入物品的个数: "; cin >> n; cout << "请输入背包的容量: "; cin >> c; for (i = 1; i <= n; i++) { cout << "请输入第" << i << "个物品的质量: "; cin >> w[i]; } for (j = 1; j <= n; j++) { cout << "输入第" << j << "个物品的价值: "; cin >> v[j]; } } int main() { input(); cout << "最大价值为:" << recursion() << endl; return 0; }
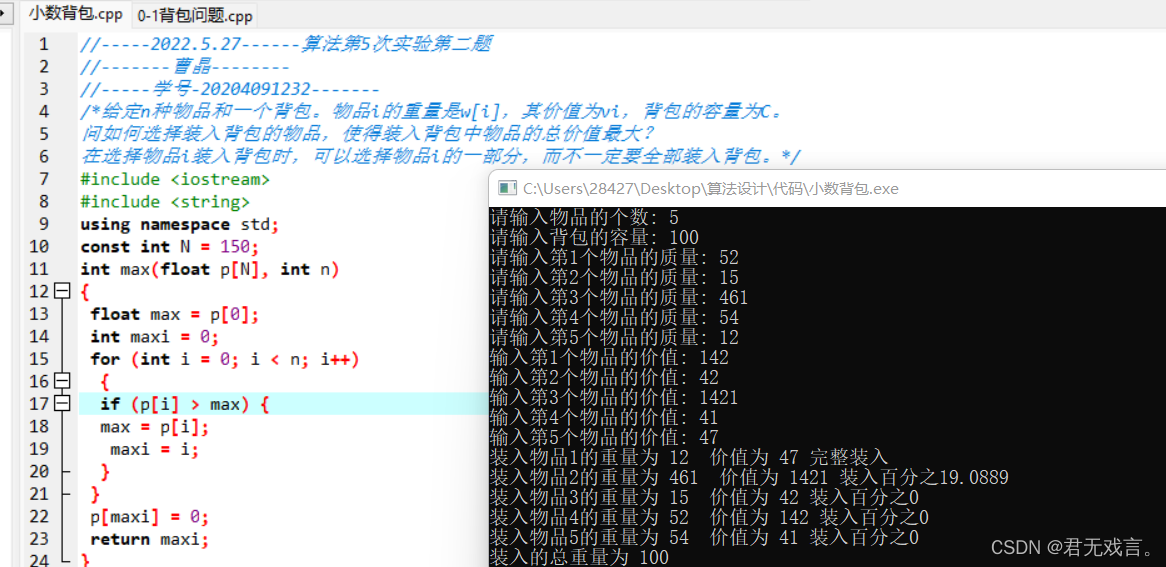
#include <iostream> #include <string> using namespace std; const int N = 150; int max(float p[N], int n) { float max = p[0]; int maxi = 0; for (int i = 0; i < n; i++) { if (p[i] > max) { max = p[i]; maxi = i; } } p[maxi] = 0; return maxi; } void traceback(int n, int c, int w[N], int v[N]) { float p[N];//价值权重 int i; int weight = 0;float value = 0;//总重量,总价值 for (i = 0; i < n; i++) //权重计算 p[i] = v[i] / (w[i]*1.0); for (i = 0; i < n; i++) { int num = max(p, n);//价值最高的下标 weight += w[num]; if (weight < c) { cout << "装入物品" << i+1 << "的重量为 " << w[num] << " 价值为 " << v[num] << " 完整装入" << endl; value += v[num]; } else if (weight > c) { float w1 = (c - (weight- w[num])) /( w[num]*1.0);//计算装入部分 cout << "装入物品" << i+1 << "的重量为 " << w[num] << " 价值为 " << v[num] << " 装入百分之" << w1*100 << endl; weight = c; value += w1 * v[num]; } else break; } cout << "装入的总重量为 " << weight << endl; cout << "装入的总价值为 " << value << endl; } int main() { int v[N]; int w[N]; int n, c; cout << "请输入物品的个数: "; cin >> n; cout << "请输入背包的容量: "; cin >> c; int i, j; for (i = 0; i < n; i++) { cout << "请输入第" << i + 1 << "个物品的质量: "; cin >> w[i]; } for (j = 0; j < n; j++) { cout << "输入第" << j + 1 << "个物品的价值: "; cin >> v[j]; } traceback(n, c, w, v); return 0; } 程序测试及运行结果: 01:
小数:
分析与讨论:
设
设子问题的最优值为其中是背包容量为,可选择物品为时0-1背包问题的最优值,就可以得到递推公式。
小数背包问题运用贪心算法 其算法与0-1背包大体相似,贪心算法解决小数背包问题与0-1背包的整数规划问题最大的不同小数背包问题需要算出每个物品的权重,通过比较权重大小,来判断放入背包的顺序,直到背包放满。 | |||||||||
算法程序设计 之 背包问题(5/8)
news2026/2/10 16:39:35
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/671802.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
CDH集群离线部署-6.3.1
1. 文件下载
CDH 安装使用到的相关文件:链接: https://pan.baidu.com/s/1xDQD1Sa8s47Qiu_EFYdhUA?pwd5mrt 提取码: 5mrt 2. 机器基础调整
所有机器都需要执行下面所有的步骤。
2.1. 准备机器
至少三台2核16G机器。
2.1.1. ECS 服务器
如果买的是 ECS 服务器&…
Apikit 自学日记:邀请成员一起协作
邀请成员一起协作
在 Apikit 中,所有的 API 接口都是以项目的方式进行管理,因此首先需要创建一个 API 管理项目。 除了创建 API 项目,还可以创建项目组来对项目进行分类或者设置统一的用户操作权限。 一、手动创建项目
进入 API 研发管理项…
有趣的笔试题——贪吃蛇游戏(确定不进来看看?)
原题 贪吃蛇游戏是一款耳熟能详的小游戏,通过上下左右控制蛇的方向,寻找吃的果子,每吃一口果子,蛇的身子会越吃越长,身子越长玩的难度就越大,不能碰墙,不能咬到自己的身体,更不能咬自…
关于springboot中前端传递多个数组以及其他参数及json在前后端转变方法技巧的记录
文末含一种json的动态解析方法,感兴趣的大佬记得看到最后评论交流 * 因公司GIS保密要求仅放部分代码在这儿
前端传输json的方法
json格式不再赘述
常规json传递
使用formData封装传递
好处就是当页面同时传递多个数组甚至是同时传递数组和参数到后台,可以自定义…
2023计算机组成原理复习【1-4】
第一章 计算机系统概述
1.计算机语言的分类:高级语言,低级语言(汇编语言与机器语言)。P8
高级语言是人类可读写的编程语言。低级语言包括汇编语言和机器语言两种。汇编语言是一种直接使用符号代替计算机指令的语言&a…
C++静态对象的移动问题
7.1返回普通的静态对象
MyString func(const char* p)
{static MyString tmp(p);return tmp;
}
int main()
{MyString s1("hello");s1func("helloworld");s1.Print();MyString s2;s2func("hello");s2.Print();return 0;
}
结果: 进…
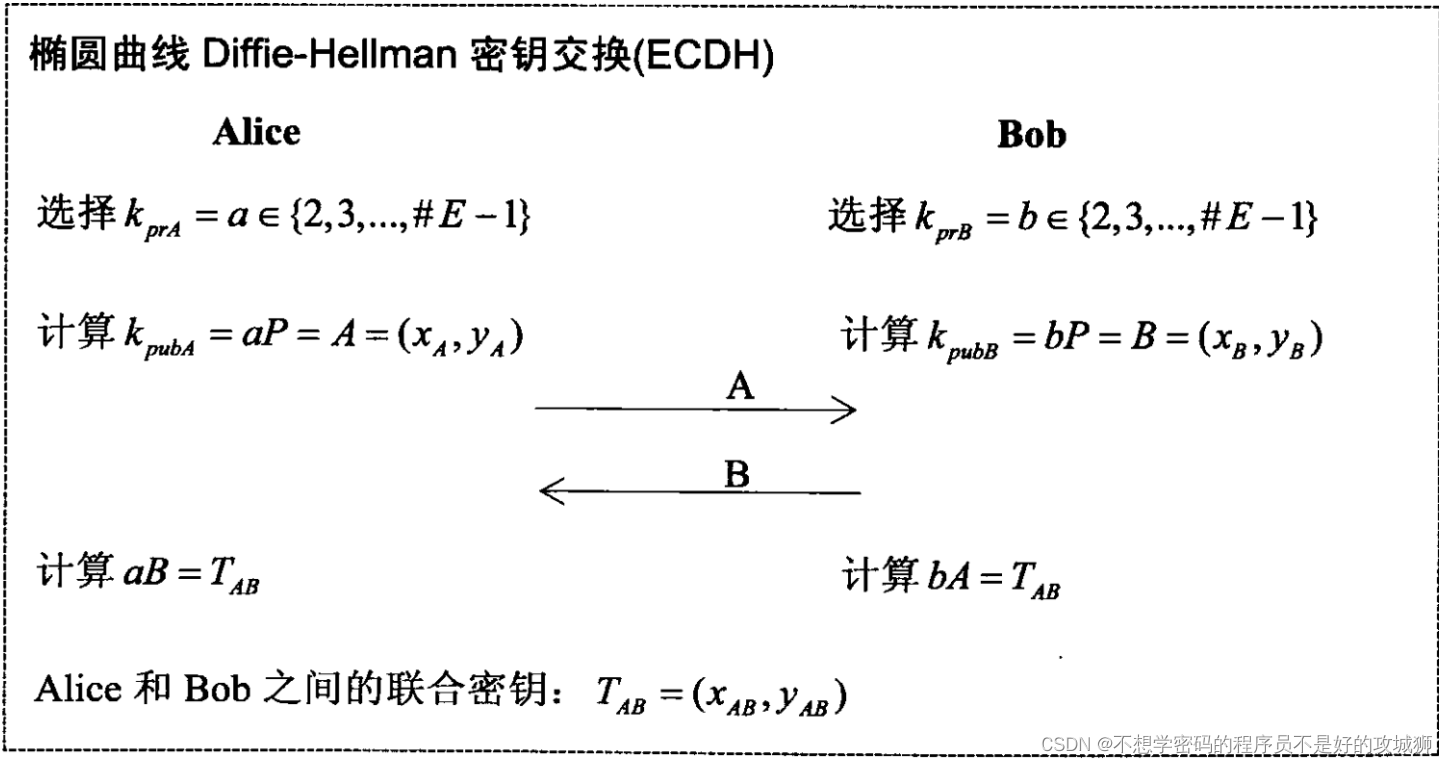
Elagamal和ECC
Elgamal加密方案 椭圆曲线加密体制
椭圆曲线应该是非奇异的,曲线的图不会自我相交或者没有顶点。
椭圆曲线的基本运运算
相异点相加PQ: 相同点相加PP: ## 椭圆曲线加解密
加解密原理:
Alice选取一个椭圆曲线 E p ( a , b ) E_p(a,b) Ep…
从0到1精通自动化测试,pytest自动化测试框架,生成html报告与html报告报错截图+失败重跑(五)
目录
一、生成html报告
1、pytest-html
2、html报告
3、指定报告路径
4、显示选项
5、更多功能
二、html报告报错截图失败重跑
1、conftest.py
2、报告展示
3、失败重试 一、生成html报告
1、pytest-html
pytest-HTML是一个插件,pytest用于生成测试结果…
C. Ranom Numbers(统计前缀)
Problem - C - Codeforces 不,不是“随机”数字。
Ranom 数字由大写拉丁字母 A 到 E 表示。此外,字母 A 的值为 1,B 为 10,C 为 100,D 为 1000,E 为 10000。
一个 Ranom 数字是一个 Ranom 数字序列。这个…
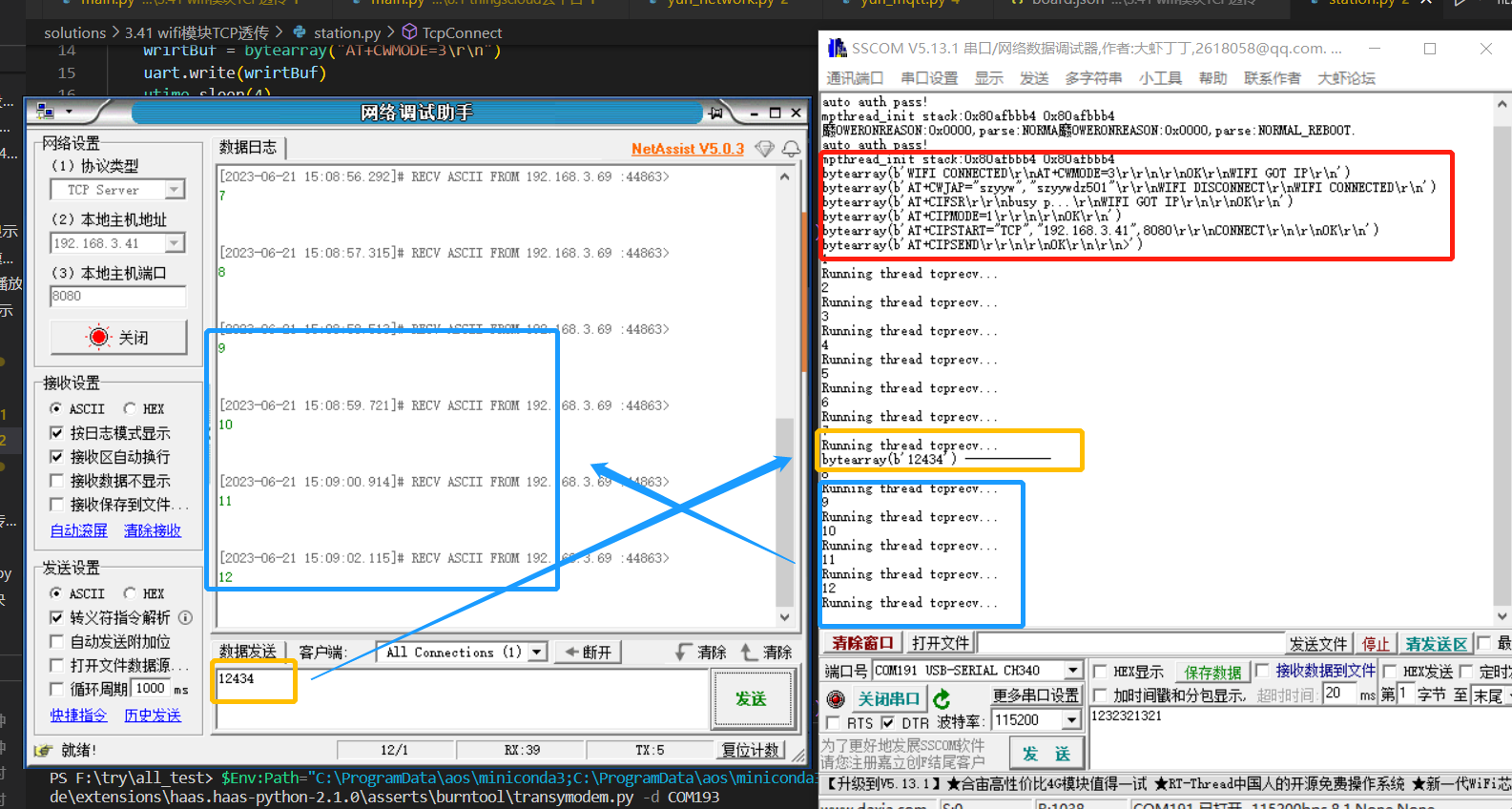
3.41 - haas506与esp8266-01s的串口通信(wifi模块)
haas506与esp8266-01s的串口通信 PC端调试wifi模块1.接线(与电脑通信)2.模式案例3.指令演示 开发板与wifi模块通信1.接线(TTL串口通信)2.代码测试 PC端调试wifi模块
esp8266-01s
1.接线(与电脑通信)
与电脑通信时引脚连接,wifi模块需要稳定3.3v供电,…
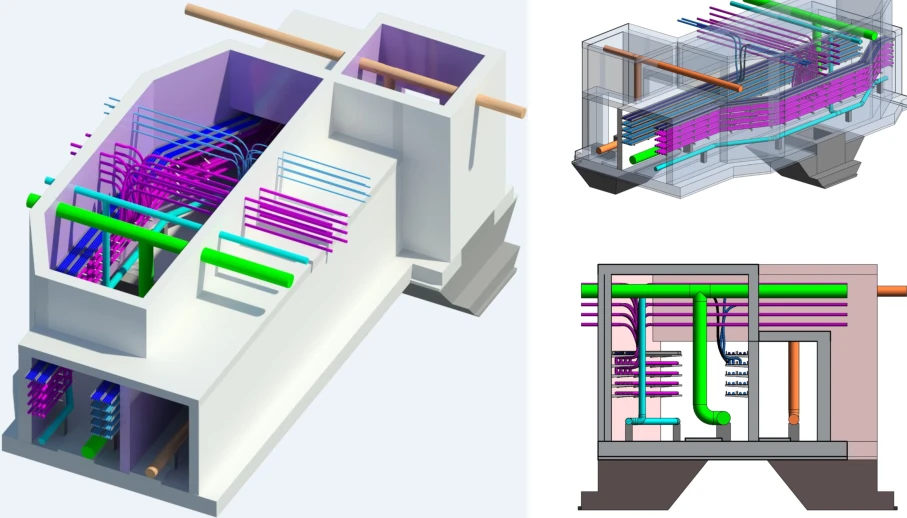
享好文 | 碰撞检查并不是BIM的目的
不知大家感觉到没有?中国很多行业都有一种惯性思维:只要是国外的就好,习惯了拿来主义。
比如前几年兴起的BIM,各种峰会论坛、培训吹得神乎其技,玩得不亦乐乎,什么协同管理、行业生态。
结果这么多年过去了…
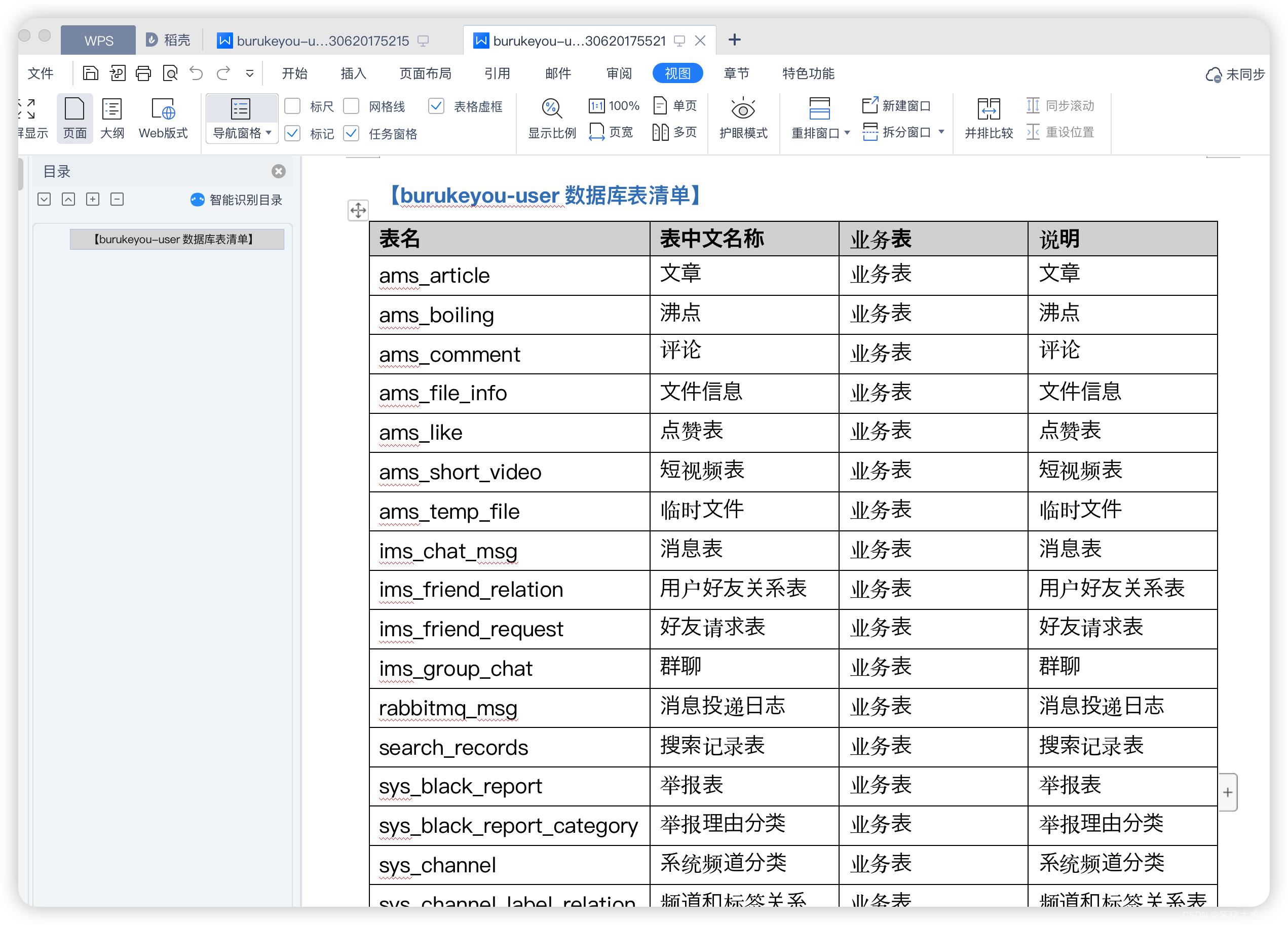
Python 动态生成系统数据库设计到word文档
背景
经常需要交付一些系统文档而且基本都是word的,其中又有系统数据库介绍模块, 看着数据库里的几百张表于是我开始怀疑人生, 所以咱手写一个
涉及知识
pymysql 操作数据库 -tkinter GUI图形库threading 线程queue 阻塞队列pandas python数据计算…
【数据结构(C++)】树型查找——二叉搜索树
目录
1. 二叉搜索树
1.1 二叉搜索树的概念
1.2 二叉搜索树类模板
1.3 二叉搜索树的操作
1.3.1 查找
1.3.2 插入
1.3.3 删除
1.4 二叉搜索树的性能分析
2. 平衡二叉树
2.1 平衡二叉树的概念
2.2 平衡二叉树类模板
2.3 二叉搜索树的插入
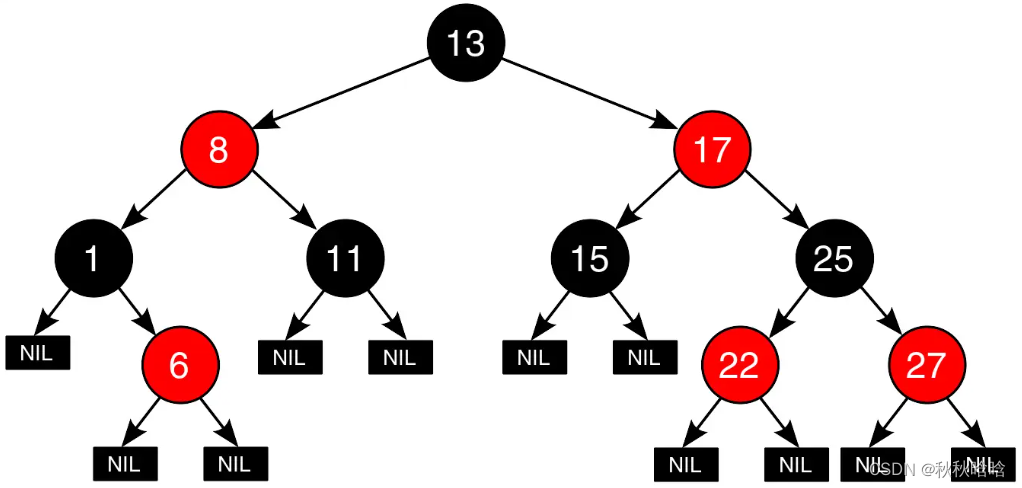
3. 红黑树
3.1 红黑树的概念…
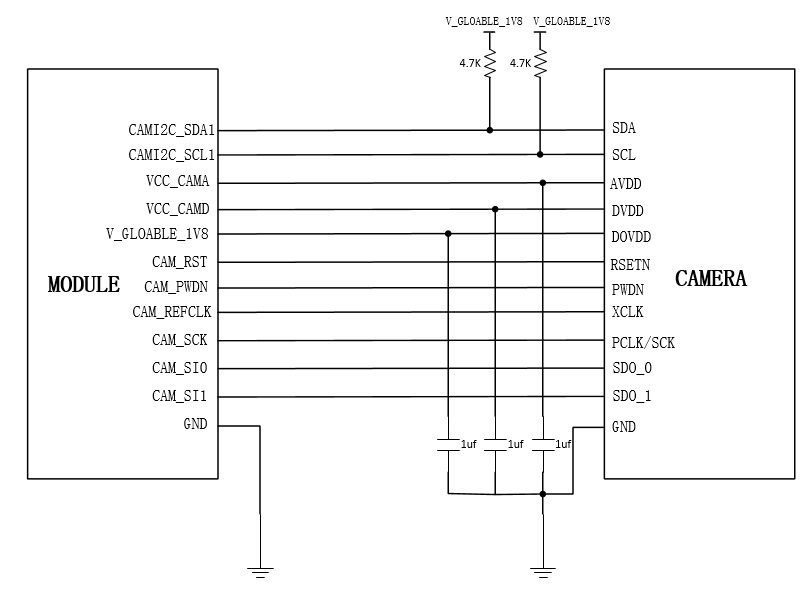
合宙Air724UG Cat.1模块硬件设计指南--Camera接口
Camera接口 简介 CAT.1模块支持一路摄像头接口,可以用于扫码,拍照应用。
特性 仅支持SPI接口实现 最高像素30W像素 支持数据格式YUV422, Y420, RAW8, RAW10 集成GC0310驱动 管脚功能 CAM_PWDN。关闭Camera,上电状态默认下拉输入。 CAM_RST。…
pg 绑定变量源码解析
pg 绑定变量相关源码解析
下面以callstmt 为例 说明一下绑定参数的执行流程(基于pg13)
整体架构 1. exec_parse_message
解析变量。 --> parse_analyze_varparams 解析绑定参数$id--->parse_variable_parameters , 把返回值paramTyp…
《Java黑皮书基础篇第10版》 第18章【习题】
Java语言程序设计 习题第十八章
18.2章节习题
18.1 什么是递归方法?什么是无限递归? 递归方法可以拆解为递和归。在Java中,大多数方法的执行都需要调用栈,来跟踪方法的调用和返回。在递的过程中,递归方法调用自身,把新的调用添…
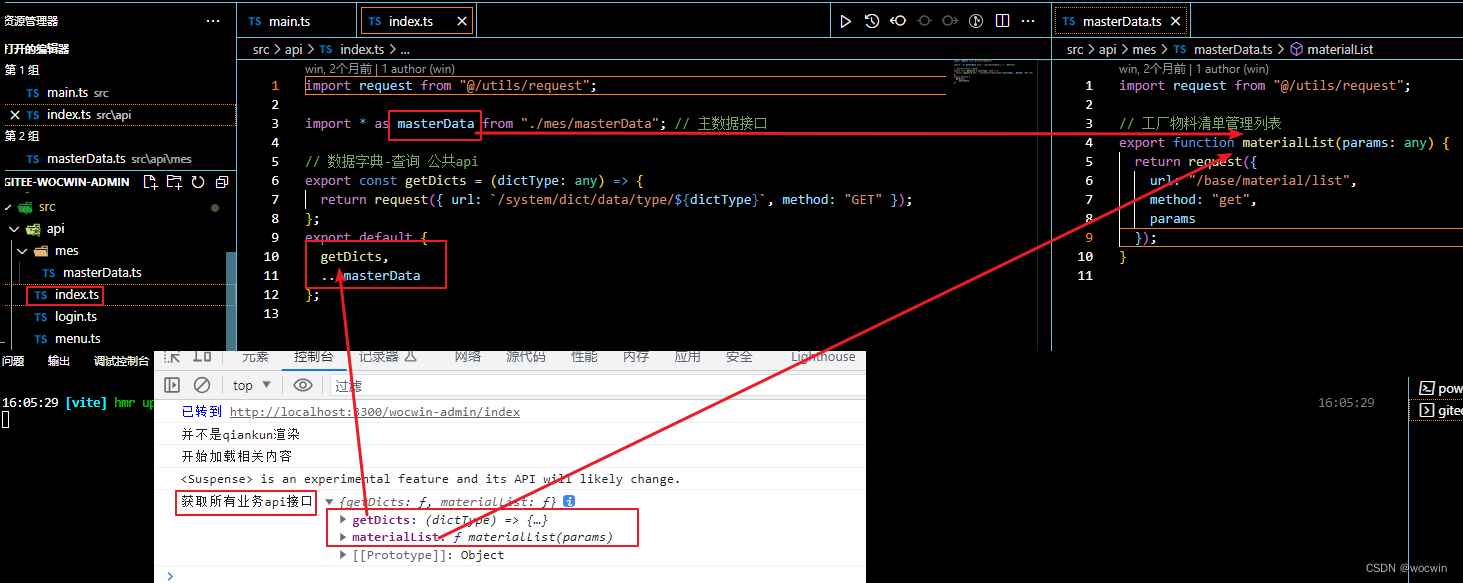
Vue3 开发语法使用总结(超详细、超基础)
前言 最近开源了一套后台管理模板Wocwin-Admin,是基于 Vue3.2、TypeScript、Vite4、Pinia、Element-Plus、Qiankun(微前端) 技术栈,借此归纳一下Vue3.2的新语法。 一、全局注册(属性/方法)
1、main.ts注册
import { createApp } from "vue";…
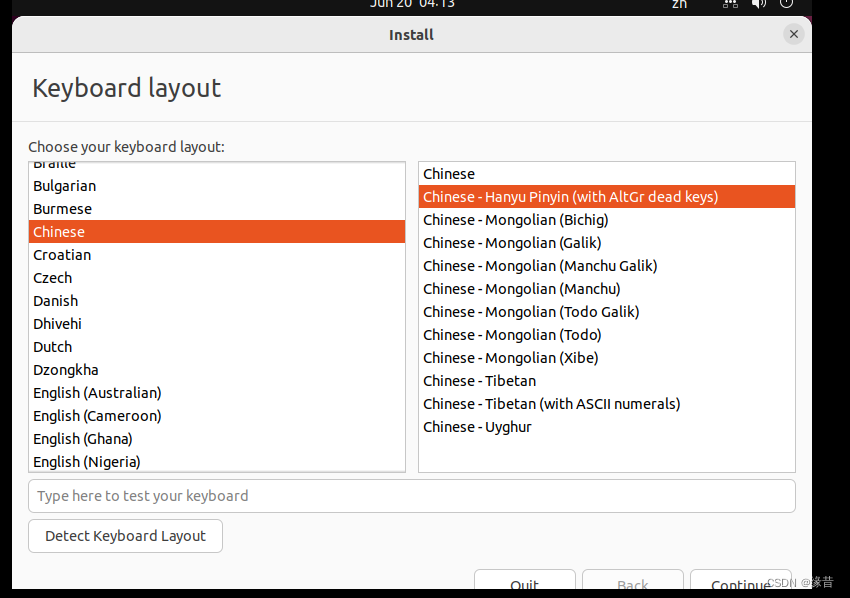
Ubuntu22 2023最新版安装教程
Ubuntu22安装教程 2023全网最新版
前置资源准备
如果选择使用虚拟机安装,那么需要准备VmwareWorkstation
在官网进行下载安装
VmwareWorkstation官网:https://www.vmware.com/products/workstation-pro/workstation-pro-evaluation.html
前置资源准备好后就可以…
【SpringCloud config分布式配置中心】—— 每天一点小知识
💧 S p r i n g C l o u d c o n f i g 分布式配置中心 \color{#FF1493}{SpringCloud config分布式配置中心} SpringCloudconfig分布式配置中心💧 🌷 仰望天空,妳我亦是行人.✨ 🦄 个人主页——微风撞见云的…