1. WarpPixelWise(求当前帧特征点位置)

1.1 函数功能

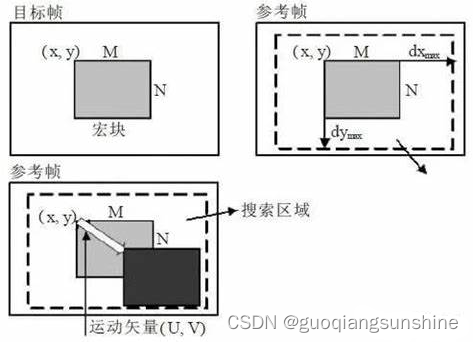
这个是将参考帧中的一个特征点周围的像素按照当前帧中的相机姿态投影到当前帧上，并将其像素值存储在一个给定的数组中。

1.2 函数输入输出

输入：函数的输入包括当前帧、参考帧、参考帧中的特征点、参考帧和当前帧的金字塔层级、半补丁尺寸
输出：一个指向输出像素值数组的指针。

1.3 算法步骤

1. 计算参考帧中特征点到参考帧相机的距离和到当前帧相机的距离；
2. 将特征点在参考帧相机坐标系下的坐标反投影到三维空间中，并根据到相机的距离缩放得到三维坐标；
3. 将三维坐标变换到当前帧相机坐标系下，并投影到当前帧图像上得到像素坐标；
4. 将像素坐标缩放到搜索层级，并对半补丁尺寸内的每个像素执行以下操作：
   • 将像素坐标变换到参考帧相机坐标系下的三维坐标；
   • 将三维坐标投影到参考帧图像上得到像素坐标；
   • 将像素坐标缩放到参考帧金字塔层级；
   • 根据双线性插值计算该像素在参考帧图像上的值，并将其存储在输出数组中。

数学公式描述如下：

$${\mathbf{p}}_{cur}={\mathbf{T}}_{cur}^{world}{\mathbf{T}}_{ref}^{worl{d}^{-1}}{\mathbf{p}}_{ref}$$

$${\mathbf{p}}_{ref}=\frac{d_{ref}}{\Vert {\mathbf{p}}_{ref}^{cam}\Vert }{\mathbf{p}}_{ref}^{cam}$$

$${\mathbf{p}}_{cur}^{search}=\frac{{\mathbf{p}}_{cur}}{2^{leve{l}_{cur}}}$$

$${\mathbf{p}}_{ele}^{search}={\mathbf{p}}_{ele}^{patch}+{\mathbf{p}}_{cur}^{search}$$

$${\mathbf{p}}_{ele}^{cam}=\frac{{\mathbf{p}}_{ele}^{search}}{2^{leve{l}_{cur}}}$$

$${\mathbf{p}}_{ele}^{world}={\mathbf{T}}_{ref}^{world}{\mathbf{T}}_{cur}^{worl{d}^{-1}}{\mathbf{p}}_{ele}^{cam}$$

$${\mathbf{p}}_{ele}^{ref}=\frac{1}{2^{leve{l}_{ref}}}{\mathbf{K}}_{ref}{\mathbf{p}}_{ele}^{cam}$$

$$\begin{gathered} I({\mathbf{p}}_{ele}^{ref})= \\ {w}_{00}I(\lfloor {\mathbf{p}}_{ele,x}\rfloor ,\lfloor {\mathbf{p}}_{ele,y}\rfloor )+w_{01}I(\lfloor {\mathbf{p}}_{ele,x}\rfloor ,\lfloor {\mathbf{p}}_{ele,y}\rfloor +1)+ \\ {w}_{10}I(\lfloor {\mathbf{p}}_{ele,x}\rfloor +1,\lfloor {\mathbf{p}}_{ele,y}\rfloor )+w_{11}I(\lfloor {\mathbf{p}}_{ele,x}\rfloor +1,\lfloor {\mathbf{p}}_{ele,y}\rfloor +1) \end{gathered}$$

其中，$\mathbf{T}$ 表示相机位姿，$\mathbf{p}$ 表示像素坐标，$d$ 表示距离，$\Vert \cdot \Vert$ 表示向量的模，$\mathbf{K}$ 表示相机内参矩阵，$I(\cdot )$ 表示图像上某个像素的值，$w_{00},w_{01},w_{10},w_{11}$ 表示双线性插值权重。

bool WarpPixelWise(const Frame& cur_frame, const Frame& ref_frame, const FeatureWrapper& ref_ftr,
    const int level_ref, const int level_cur, const int half_patch_size, uint8_t* patch) {
  double depth_ref = (ref_frame.pos() - ref_ftr.landmark->pos()).norm();
  double depth_cur = (cur_frame.pos() - ref_ftr.landmark->pos()).norm();

  // back project to 3D points in reference frame
  Eigen::Vector3d xyz_ref;
  ref_frame.cam()->backProject3(ref_ftr.px, &xyz_ref);
  xyz_ref = xyz_ref.normalized() * depth_ref;

  // project to current frame and convert to search level
  Eigen::Vector3d xyz_cur = cur_frame.T_cam_world() * (ref_frame.T_cam_world().inverse()) * xyz_ref;
  Eigen::Vector2d px_cur;
  cur_frame.cam()->project3(xyz_cur, &px_cur);
  Eigen::Vector2d px_cur_search = px_cur / (1 << level_cur);

  // for each pixel in the patch(on search level):
  // - convert to image level
  // - back project to 3D points
  // - project to ref frame and find pixel value in ref level
  uint8_t* patch_ptr = patch;
  const cv::Mat& img_ref = ref_frame.img_pyr_[level_ref];
  const int stride = img_ref.step.p[0];

  for (int y = -half_patch_size; y < half_patch_size; ++y) {
    for (int x = -half_patch_size; x < half_patch_size; ++x, ++patch_ptr) {
      const Eigen::Vector2d ele_patch(x, y);
      Eigen::Vector2d ele_search = ele_patch + px_cur_search;
      Eigen::Vector3d ele_xyz_cur;
      cur_frame.cam()->backProject3(ele_search * (1 << level_cur), &ele_xyz_cur);
      ele_xyz_cur = ele_xyz_cur.normalized() * depth_cur;
      Eigen::Vector3d ele_xyz_ref =
          ref_frame.T_cam_world() * (cur_frame.T_cam_world().inverse()) * ele_xyz_cur;
      Eigen::Vector2d ele_ref;
      ref_frame.cam()->project3(ele_xyz_ref, &ele_ref);
      ele_ref = ele_ref / (1 << level_ref);

      const int xi = std::floor(ele_ref[0]);
      const int yi = std::floor(ele_ref[1]);
      if (xi < 0 || yi < 0 || xi + 1 >= img_ref.cols || yi + 1 >= img_ref.rows) {
        VLOG(200) << "ref image: col-" << img_ref.cols << ", row-" << img_ref.rows;
        VLOG(200) << "xi: " << xi << ", "
                  << "yi: " << yi;
        return false;
      } else {
        const float subpix_x = ele_ref[0] - xi;
        const float subpix_y = ele_ref[1] - yi;
        const float w00 = (1.0f - subpix_x) * (1.0f - subpix_y);
        const float w01 = (1.0f - subpix_x) * subpix_y;
        const float w10 = subpix_x * (1.0f - subpix_y);
        const float w11 = 1.0f - w00 - w01 - w10;
        const uint8_t* const ptr = img_ref.data + yi * stride + xi;
        *patch_ptr = static_cast<uint8_t>(
            w00 * ptr[0] + w01 * ptr[stride] + w10 * ptr[1] + w11 * ptr[stride + 1]);
      }
    }
  }

  return true;
}

2. GetWarpMatrixAffine(计算 当前帧->参考帧 仿射变换矩阵)

2.1 函数功能

函数作用是计算从当前帧到参考帧的仿射变换矩阵，使得参考帧中的一个特征点在当前帧中的投影与当前帧中的相应补丁重合。

2.2 函数输入输出

输入：函数的输入包括参考帧和当前帧的相机参数、参考帧中的特征点、特征点的方向向量、特征点到参考帧相机的距离、当前帧和参考帧之间的位姿变换、参考帧的金字塔层级。
输出：一个指向输出仿射变换矩阵的指针。

2.3 算法步骤

函数的实施步骤如下：

1. 根据特征点的方向向量和距离计算三维坐标；
2. 在参考帧中沿着水平和垂直方向各移动半个补丁大小，将移动后的像素坐标反投影到三维空间中得到两个方向上的三维向量；
3. 将三维向量变换到当前帧相机坐标系下，并将其投影到当前帧上得到三个像素坐标；
4. 根据三个像素坐标计算仿射变换矩阵。

数学公式描述如下：

$$\begin{array}{rl}{\mathbf{x}}_{ref}& ={\mathbf{f}}_{ref}{d}_{ref}\\ {\mathbf{x}}_{du,ref}& ={\mathbf{J}}_{du,ref}{\mathbf{x}}_{ref}\\ {\mathbf{x}}_{dv,ref}& ={\mathbf{J}}_{dv,ref}{\mathbf{x}}_{ref}\\ {\mathbf{x}}_{cur}& =T_{cur\_ref}{\mathbf{x}}_{ref}\\ {\mathbf{x}}_{du,cur}& =T_{cur\_ref}{\mathbf{x}}_{du,ref}\\ {\mathbf{x}}_{dv,cur}& =T_{cur\_ref}{\mathbf{x}}_{dv,ref}\\ {\mathbf{A}}_{cur\_ref}& =\left[\begin{array}{cc}\frac{{\mathbf{x}}_{du,cur}-{\mathbf{x}}_{cur}}{kHalfPatchSize}& \frac{{\mathbf{x}}_{dv,cur}-{\mathbf{x}}_{cur}}{kHalfPatchSize}\end{array}\right]\end{array}$$

其中，${\mathbf{f}}_{ref}$ 表示特征点的方向向量，$d_{ref}$ 表示特征点到参考帧相机的距离，${\mathbf{x}}_{ref}$ 表示特征点在参考帧相机坐标系下的三维坐标，${\mathbf{x}}_{du,ref}$ 和 ${\mathbf{x}}_{dv,ref}$ 表示在水平和垂直方向上移动半个补丁尺寸后在参考帧中的三维坐标，${\mathbf{J}}_{du,ref}$ 和 ${\mathbf{J}}_{dv,ref}$ 分别表示在水平和垂直方向上移动半个补丁尺寸后对应的像素坐标在参考帧相机坐标系下对应的三维向量，$T_{cur\_ref}$ 表示当前帧到参考帧之间的位姿变换，${\mathbf{x}}_{cur}$、${\mathbf{x}}_{du,cur}$ 和 ${\mathbf{x}}_{dv,cur}$ 分别表示将 ${\mathbf{x}}_{ref}$、${\mathbf{x}}_{du,ref}$ 和 ${\mathbf{x}}_{dv,ref}$ 变换到当前帧相机坐标系下后得到的三维坐标，$\frac{{\mathbf{x}}_{du,cur}-{\mathbf{x}}_{cur}}{kHalfPatchSize}$ 和 $\frac{{\mathbf{x}}_{dv,cur}-{\mathbf{x}}_{cur}}{kHalfPatchSize}$ 分别表示在水平和垂直方向上移动半个补丁尺寸后对应像素坐标在当前帧相机坐标系下对应的三维向量，${\mathbf{A}}_{cur\_ref}$ 表示从当前帧到参考帧的仿射变换矩阵。

void GetWarpMatrixAffine(const CameraPtr& cam_ref, const CameraPtr& cam_cur,
    const Eigen::Ref<Keypoint>& px_ref, const Eigen::Ref<BearingVector>& f_ref,
    const double depth_ref, const Transformation& T_cur_ref, const int level_ref,
    AffineTransform* A_cur_ref) {
  CHECK_NOTNULL(A_cur_ref);

  // Compute affine warp matrix A_ref_cur
  const int kHalfPatchSize = 5;
  const Position xyz_ref = f_ref * depth_ref;
  Position xyz_du_ref, xyz_dv_ref;
  // NOTE: project3 has no guarantee that the returned vector is unit length
  // - for pinhole: z component is 1 (unit plane)
  // - for omnicam: norm is 1 (unit sphere)
  cam_ref->backProject3(
      px_ref + Eigen::Vector2d(kHalfPatchSize, 0) * (1 << level_ref), &xyz_du_ref);
  cam_ref->backProject3(
      px_ref + Eigen::Vector2d(0, kHalfPatchSize) * (1 << level_ref), &xyz_dv_ref);
  if (cam_ref->getType() == Camera::Type::kPinhole) {
    xyz_du_ref *= xyz_ref[2];
    xyz_dv_ref *= xyz_ref[2];
  } else {
    xyz_du_ref.normalize();
    xyz_dv_ref.normalize();
    xyz_du_ref *= depth_ref;
    xyz_dv_ref *= depth_ref;
  }

  Keypoint px_cur, px_du_cur, px_dv_cur;
  cam_cur->project3(T_cur_ref * xyz_ref, &px_cur);
  cam_cur->project3(T_cur_ref * xyz_du_ref, &px_du_cur);
  cam_cur->project3(T_cur_ref * xyz_dv_ref, &px_dv_cur);
  A_cur_ref->col(0) = (px_du_cur - px_cur) / kHalfPatchSize;
  A_cur_ref->col(1) = (px_dv_cur - px_cur) / kHalfPatchSize;
}

3. GetWarpMatrixAffine(计算 当前帧->参考帧 仿射变换矩阵)

3.1 函数功能

这个函数的作用是计算在哪个金字塔层级上搜索匹配点可以获得最佳性能。

3.2 函数输入输出

输入：它的输入包括一个仿射变换矩阵和一个最大金字塔层级。
输出：输出为一个金字塔层级。

3.3 算法步骤

1. 计算仿射变换矩阵的行列式D；
2. 如果D大于3.0并且搜索层级小于最大金字塔层级，则将搜索层级加1，同时将D乘以0.25，直到D小于等于3.0或者搜索层级达到最大金字塔层级。

数学公式描述如下：

s e a r c h _ l e v e l = min ⁡ ( max ⁡ _ l e v e l , max ⁡ { n ∣ D ( A c u r _ r e f ) > 3. 0 n } ) search\_level = \min(\max\_level, \max\{n|D(A_{cur\_ref}) > 3.0^n\}) search_level=min(max_level,max{n∣D(Acur_ref​)>3.0n})

其中，$D(A_{cur\_ref})$ 表示仿射变换矩阵 $A_{cur\_ref}$ 的行列式。

这个函数的原理是根据仿射变换矩阵的不确定性来选择搜索的金字塔层级。当仿射变换矩阵越不确定时，需要在更高的金字塔层级上进行搜索，以获得更好的匹配性能。而当仿射变换矩阵越确定时，可以在更低的金字塔层级上进行搜索，以提高计算效率。

int GetBestSearchLevel(const AffineTransform& A_cur_ref, const int max_level) {
  // Compute patch level in other image
  int search_level = 0;
  double D = A_cur_ref.determinant();
  while (D > 3.0 && search_level < max_level) {
    search_level += 1;
    D *= 0.25;
  }
  return search_level;
}