论文题目：重新思考注意力在时间序列预测任务中应用

作者单位：亚马逊访问学者、亚马逊云科技

摘要：

基于Transformer的一系列方法在长时间序列预测任务中很有效，除了在时域部分学习注意力外，最近的工作也在频域中探索注意力的学习，（使用傅立叶变换、小波变换）。使得模型能够学习季节性的特征。本文试图去理解注意力模型之间的关系，即使这些模型被应用在不同的时域和频域中。理论上，注意力机制在不同的域是等效的，因为，使用的是相同的线性核。实验结果证明，本文分析了注意力模型在不同的域中有着不同的表现，这些表现也是通过接入不同的合成实验，季节、趋势、噪声，并且特别强调了softmax操作的重要性。也是通过结合理论和实验的分析，本文提出了TDformer，趋势分解的Transformer。第一次使用季节趋势分解，然后结合多层感知机，用于预测傅立叶注意力的趋势组成，而傅立叶注意力是用来预测季节成分从而获取最终的预测结果。在benchmark 的时间序列数据集上的实验显示 TDFormr实现了sota的结果，与现有的注意力模型相比。

季节可以理解为周期

引言

Transformer在时间序列预测任务中表现很棒，它从自然语言处理到CV迁移到时间序列预测，长距离依赖的获取能力使得它在时间序列预测任务中表现也很棒。部分工作使用的是原始的Transformer机制，在时域上进行计算，而最近出现的各种不同的Transformer的变体都是在频域上进行计算。（傅立叶域或者是小波域），用于更好的建模全局特征。

尽管它很棒，但仍然缺乏首屈一指的规则来选择在哪个域，哪个注意力是最好的。本文更好的理解了以下几个问题：在某个域内，注意力学习是否比其他的方式提供了更丰富的特征表征？如果是这样的，怎样实现的呢？本文中显示了数学公式化的线性条件，使得时间域和频域中的注意力学习有着相同的表征能力。接着，由于softmax的非线性映射和正则化，理论上的线性相等并不成立。更特别的是，注意力模型在不同域上表现出不同的实验优势。这个发现揭示了面对不同的任务场景如何选择更好的注意力模型。基于这些insight结果，证明方法的sota。

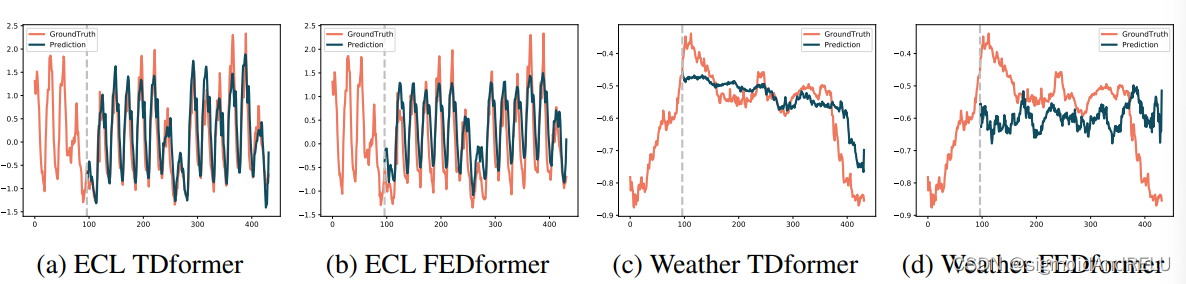
可视化第一张图，显示了TDFormer同FEDformer的性能对比，在Weather数据集上有着更优的效果。

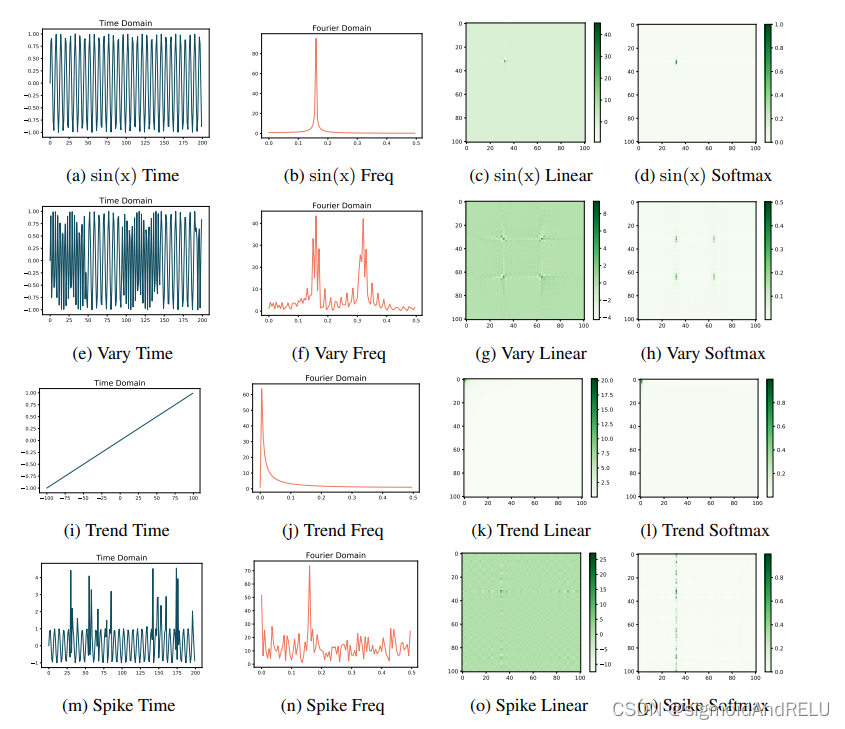
更具体的，三个发现：
（1）具有强季节性的数据，频域注意力模型的能力较时域注意力模型而言更为好用，因为softmax将傅立叶空间的频域的主频信号做了放大。
（2）对于有趋势的数据，注意力模型通常表现出较差的泛化能力，这是因为注意力是通过内插进行建模，而非向外推断上下文。所以积极探索趋势型数据的季节趋势非常有必要。
（3）对于具有噪声尖峰的数据集，频域注意力模型会更加的robust，因为尖峰数据的高频幅值小，通过sofrmax操作可以将它滤掉。

所以，多样化的注意力模块在季节型和趋势型的数据上表现不同，所以TDformer在最开始就将context 时间序列分解为趋势和季节，两部分。使用多层感知机预测未来趋势，使用傅立叶注意力机制预测有季节性的部分数据，将这两部分预测结果融合为一体，得到最后的预测结果。
综上，本文的贡献如下：
（1）理论上证明注意力机制在线性条件下，时域和频域上有着相同的表征能力。
（2）实验分析了注意力模型在不同的合成数据特征的不同域中，softmax的非线性作用很重要。使得级联网络需要分解信号，按照不同种类使用不同方法处理。
（3）提出的TDformer使用MLP+Fourier attention 实现了sota效果。

不同域中注意力的线性相等

来个经典自注意力：
$o(q,k,v)=\sigma(\frac{qk^{T}}{\sqrt{d_q}})v$
这里考虑激活函数 $\sigma()$ 如果是softmax函数，称为softmax注意力，若是线性层，就变成线性注意力，
定义3.1：时间域的注意力机制，所有的qkv都在时间域内打转。
定义3.2：傅立叶频域的注意力机制，所有的qkv都通过傅立叶变换来求取，最后使用傅立叶反变换将数据从频域转回时间域。
看公式较为清楚：
$o(q,k,v)=F^-1((\sigma(\frac{F(q) \overline{F(k)}^T)}{\sqrt{d_q}})F(v))$
定义3.3：小波域中的注意力机制，这个得，看公式吧
$o(q,k,v)=W^-1((\sigma(\frac{W(q) \overline{W(k)}^T)}{\sqrt{d_q}})W(v))$
其中F，W指的是傅立叶变换，小波变换，而-1指代逆变换，其实二者只是基底不同。