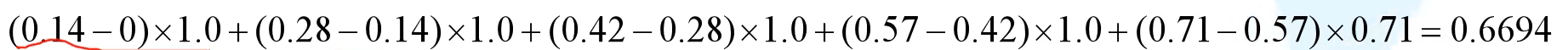下面把构建神经网络的“层”实现为一个类。这里所说的“层”是神经网络中功能的单位。

下面先从一些简单的层开始介绍

乘法层的实现

层的实现中有两个共通的方法(接口)forward()和backward()。
forward() 对应正向传播
backward() 对应反向传播

现在来实现乘法层。看下面代码

class MulLayer:
	def __init__(self):
		self.x = None
		self.y = None
	
	def forward(self, x, y):
		self.x = x
		self.y = y
		out = x * y
		return out

	def backward(self, dout):
		dx = dout*self.y # 翻转x和y
		dy = dout*self.x

		return dx,dy

backward()将从上游传来的导数(dout)乘以正向传播的翻转值，然后传给下游。

下面就使用MulLayer实现前面的购买的例子(2个苹果和消费税)。看图：

通过乘乘法层，上图的正向传播可以像下面这样实现：

apple = 100
apple_num = 2
tax = 1.1

# layer
mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()

#forward
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price ,tax)
print(price)

求各个变量的导数可由backward()求出

#backward
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

print(dapple, dapple_num, dtax)

此外，要注意backward()的参数中需要输入“关于正向传播时的输出变量的导数”。

加法层的实现

下面来实现加法节点的加法层

class AddLayer:
	def __init__(self):
		pass

	def forward(self, x, y):
		out = x+y
		return out

	def backward(self, dout):
		dx = dout*1
		dy = dout*1
		return dx,dy

下面使用加法层和乘法层，实现下图的例子：

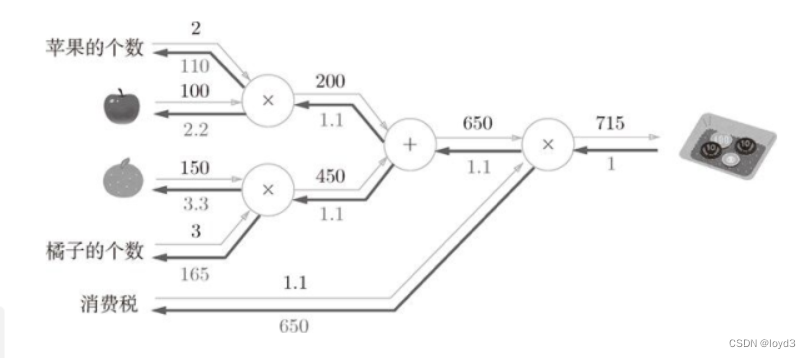
实现代码如下：

apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1

# layer
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
orange_price = mul_orange_layer.forward(orange, orange_num)
all_price = add_apple_orange_layer.forward(apple_price, orange_price)
price = mul_tax_layer.forward(all_price, tax)

#backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)
dorange, dorange_num = nul_orange_layer.backward(dorange_price)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

print(price)
print(dapple_num, dapple, dorange, dorange_num, dtax)

综上，计算图中层的实现非常简单，使用这些层可以进行复杂的导数计算。

激活函数层的实现

这里把构成神经网络的层实现为一个类。先来实现激活函数的ReLU层和Sigmoid层。

现在来实现ReLU层。在神经网络的层的实现中，一般假定 forward()和tackerd0 的参数是NumPy数组。代码如下：

class Relu:
	def __init__(self):
		self.mask = None

	def forward(self, x):
		self.mask = (x <= 0)
		out = x.copy()
		out[self.mask] = 0

		return out

	def backward(self, dout):
		dout[self.mask] = 0
		dx = dout
		
		return dx
	

Relu类有实例变量mask。这个变量mask是由True/False构成的NumPy数组，它会把正向传播时的输人x的元素中小于等于0的地方保存为True，其他地方(大于0的元素)保存为False。如下例所示，mask变量保存了由True/False构成的NumPy数组

>>> x= np.array( [[1.0,-0.5],[-2.0，3.0]] )
>>>print(x)
[[1. -0.5]
[-2、 3.]]
>>>mask=(x<=0)
>>>print(mask)
[[False True]
[True False]]

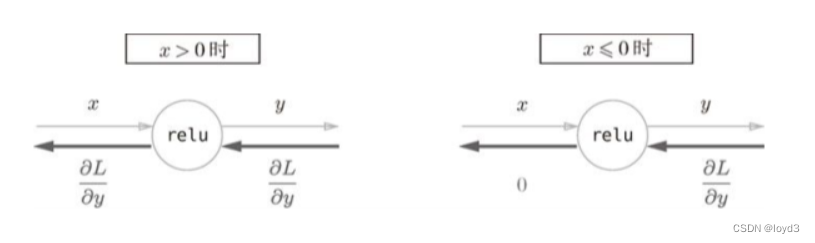
如果正向传播时的输入值小于等于0, 则反向传播的值为0,
反向传播中会使用正向传播时保存的mask，
将从上游传来的dout的mask中的元素为True的地方设为0。 (关键思路）

Sigmoid层

计算图表示的话，如下：

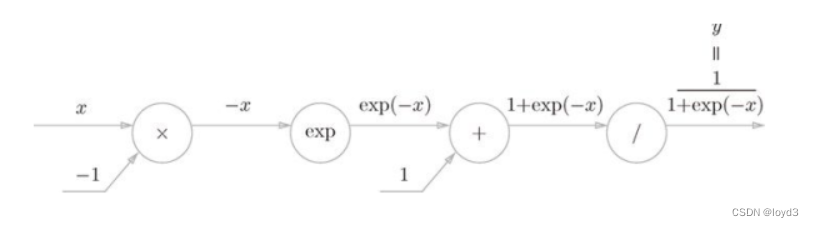
Sigmoid层包括反向传播的计算图如下：

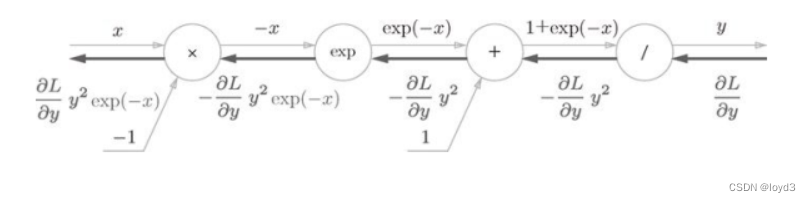
上面可以简化为

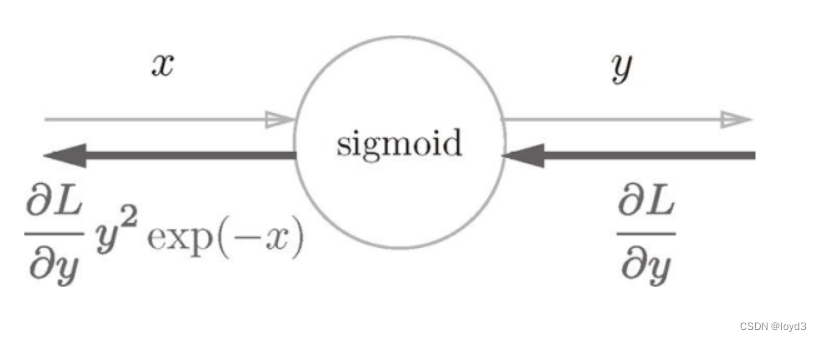
这样通过对节点进行集约化，可以不用在意Sigmoid层中琐碎的细节，而只需要专注它的输入和输出

另外，该结果可以进一步整理如下：

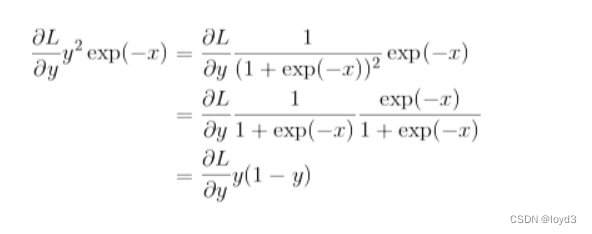
下面用Python来实现Sigmoid层，代码如下：

class Sigmoid:
	def __init__(self):
		self.out = None

	def forward(self,x):
		out = 1 / (1+np.exp(-x))
		self.out = out
		return out

	def backward(self, dout):
		dx = dout * (1.0 - self.out)*self.out
		return dx