前言

2023-6-19 15:49:17

以下内容源自《网络安全》
仅供学习交流使用

推荐

第2章 作业（2456）【网络安全】

第3章 作业

2

3.2什么是MAC?

MAC：消息认证码，一种认证技术利用私销产生一小块数据，将其附到消息上。

6

3.6公钥密码系统的基本组成元素是什么?

公钥密码系统的基本组成元素：
①明文（算法的输入）②加密算法（加密解法对明文进行各种形式变换。③公钥和私钥（算法的输入）
④密文（算法的输出）⑤解密算法（接收密文和匹配的密钥）

8

3.8私钥和密钥之间有什么区别?

密钥：传统密码算法中使用的密钥
公私钥：用于公钥密码的两个密钥被称为公钥和私钥．

E

3.14如图3.9所示,对下列值使用RSA算法进行加密和解密:

a. 	p=3;		q=11，	c=7;		M=5
b.	p=5;		q=11，	e=3:		M=9
e.	p=17;		q=31，	e=7;		M=2

提示:解密并不像你想象的那么困难,可以使用一些技巧。

a .( p=3,q=11, e=7, M = 5 )
加密： n = pq =3×11=33
 c =M^e( mod n )=5^7(mod33)=14
解密：Φ(n)=(p -1)(q-1)=2x10=20
 de mod Φ(n)=1 => d =3 
 M = c^d mod n =14^3 mod 33=5 
 b.(p =5.q=11, e =3, M =9)
加密： n =pq=55
c= M^e(mod n)=9^3(mod55)=14
解密：Φ(n=( p -1)(q-1)=4x10=40
 de mod Φ(n)=1 => d =27 
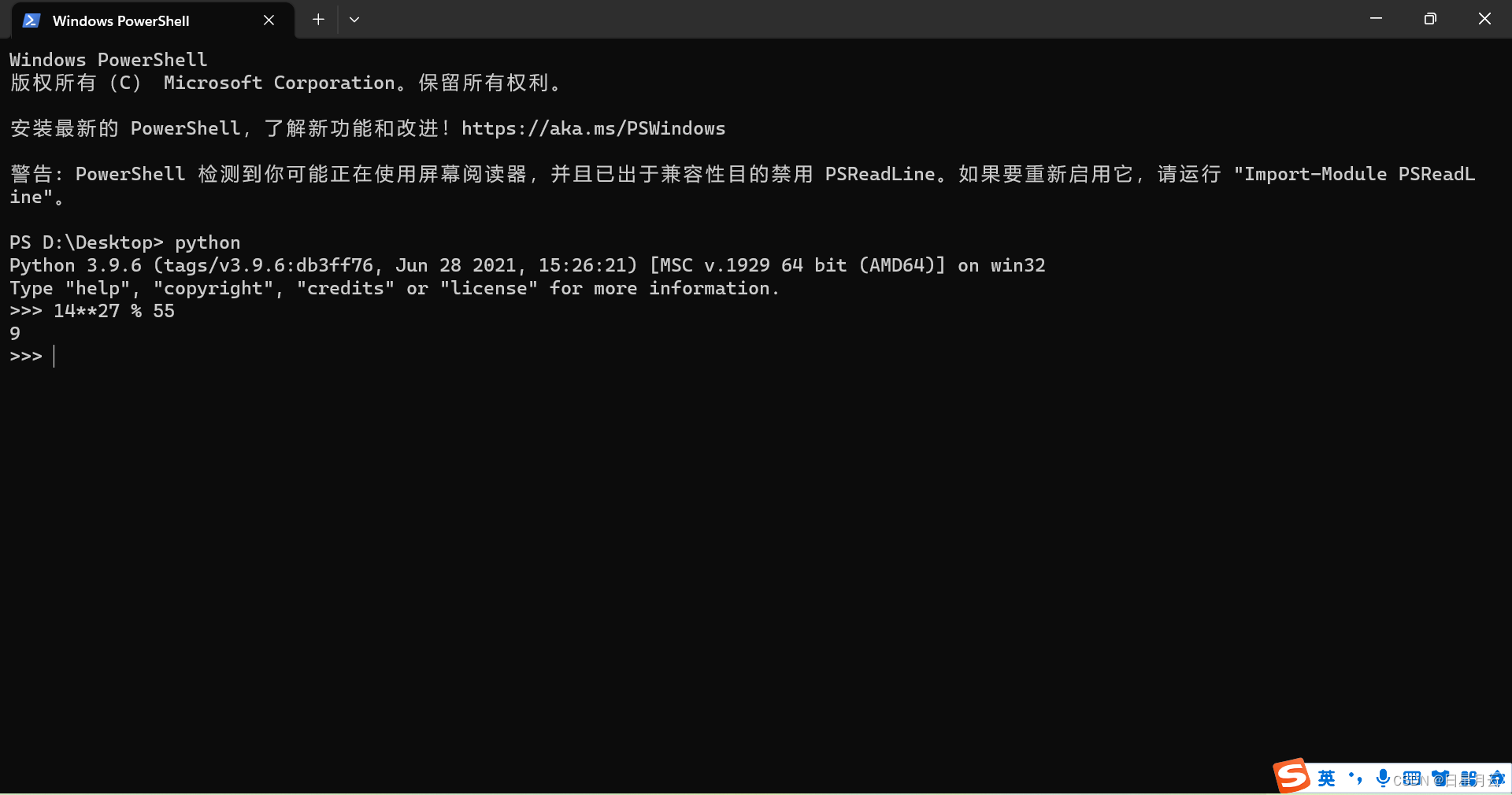
 M = c^d mod n =14^27 mod 55=9 
 e .(p =17, q =31, e =7, M =2)
 加密：n = pq =17x31=527
 c = M^e ( mod n )=2^7(mod 57)=128
解密：Φ(n)=( p -1)(q+1)=16x30=480
 de mod Φ(n)=1=>  d =343
 M = c^d mod n =128^343 mod 527=2

F

3.15在使用RSA的公钥系统中，你可截获发送给用户的密文C=10，并且已知他的公钥是e=5，n=35。明文M是什么?

3.15 c =10.e=5.n=35
 n = pq =35 p =5.q=7
Φ(n)=(p-1)(1-1)=4x6=24 
de moΦ(n)=1 => d =5
 M = c^d mod n =10^5 mod 35=5

如何不用计算机计算求模

主要利用以下公式

	(a * b) mod n 
=	[(a mod n) * (b mod n)] mod n

	(a + b) mod n 
=	[(a mod n) + (b mod n)] mod n

计算：M = c^d mod n
举例：14²⁷ mod 55=9

计算起来也是比较麻烦的
乘法只要计算2位数的，不需要计算太大的数
特别难算的就别计算了

	14^27 mod 55
=	[(14^2 mod 55)^13 * (14 mod 55)] mod 55
=	(31^13*14) mod 55
=	[(31^2 mod 55)^6 31*14) mod 55  		//31**2%55=26
=`	(26^6 mod 55 * 434 mod 55 )mod 55
=	[(26^2 mod 55)^3 * 49] mod 55			//26**2%55=26
=	(16^3 mod 55 * 49) mod 55
=	(256 mod 55 * 16*49 mod 55) mod 55
=	(36*14) mod 55
=	504 mod 55
=	9

每一次计算后，都有mod n
因为结果必须是小于n
小学知识：余数必须比除数小

结果：9

计算：de mod Φ(n)=1=> d =？
举例： de mod Φ(n)=1=> d =343（e=7 Φ(n)=480)

d*7 mod 480=1
(d*7-1) mod 480=0
(d*7-1)=480z //z是整数
d=(480z+1)/7
z用枚举法举例即可
z=1,d=68.7
z=2,d=137.2
z=3,d=205.8
z=4,d=274.4
z=5,d=343

d=343

最后

2023-6-19 16:55:26

你对我百般注视，
并不能构成万分之一的我，
却是一览无余的你。

祝大家逢考必过
点赞收藏关注哦