题目：

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

题解：

class solution {
public:
    int getdepth(TreeNode* node) {
        if (node == NULL) return 0;
        int leftdepth = getdepth(node->left);       // 左
        int rightdepth = getdepth(node->right);     // 右
        int depth = 1 + max(leftdepth, rightdepth); // 中
        return depth;
    }
    int maxDepth(TreeNode* root) {
        return getdepth(root);
    }
};

题目：

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

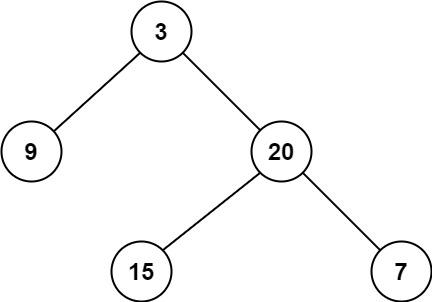
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

树中节点数的范围在 [0, 105] 内
-1000 <= Node.val <= 1000

题解：

class Solution {
public:
    int getDepth(TreeNode* node) {
        if (node == NULL) return 0;
        int leftDepth = getDepth(node->left);           // 左
        int rightDepth = getDepth(node->right);         // 右
                                                        // 中
        // 当一个左子树为空，右不为空，这时并不是最低点
        if (node->left == NULL && node->right != NULL) { 
            return 1 + rightDepth;
        }   
        // 当一个右子树为空，左不为空，这时并不是最低点
        if (node->left != NULL && node->right == NULL) { 
            return 1 + leftDepth;
        }
        int result = 1 + min(leftDepth, rightDepth);
        return result;
    }

    int minDepth(TreeNode* root) {
        return getDepth(root);
    }
};

题目：

222. 完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

输入：root = [1,2,3,4,5,6]
输出：6

示例 2：

输入：root = []
输出：0

示例 3：

输入：root = [1]
输出：1

提示：

树中节点的数目范围是[0, 5 * 104]
0 <= Node.val <= 5 * 104
题目数据保证输入的树是 完全二叉树

题解：

class Solution {
private:
    int getNodesNum(TreeNode* cur) {
        if (cur == NULL) return 0;
        int leftNum = getNodesNum(cur->left);      // 左
        int rightNum = getNodesNum(cur->right);    // 右
        int treeNum = leftNum + rightNum + 1;      // 中
        return treeNum;
    }
public:
    int countNodes(TreeNode* root) {
        return getNodesNum(root);
    }
};

欢迎点赞，收藏，评论，你的鼓励就是我创作的最大动力！(๑╹◡╹)ﾉ"""