1.问题描述

整数数组按升序排列，数组中的值互不相同。

假设数组在预先未知的某个点上进行了旋转。

如数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2]。

搜索一个给定的目标值，如果数组中存在目标值，则返回它的索引，否则返回 -1 。

算法时间复杂度必须是 O(logn) 级别。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

2.难度等级

medium。

3.热门指数

★★★★☆

出题公司：腾讯音乐。

4.解题思路

思路

本题是数组，而且要求时间复杂度为 O(logn) 。应该能够自然想到二分查找。

但是直接使用二分查找行不行呢？我们看一看下面这个例子：

在数组 [3 4 5 6 7 8 0 1 2 3] 中使用二分查找 0。

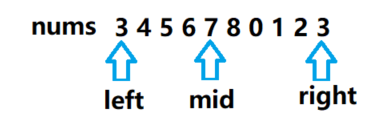
在这里插入图片描述
第一次循环时，left = 0，right = 9，得到 mid = 4，此时nums[mid] = 7，target < nums[mid] ，所以应该有 right = mid - 1。因此得到

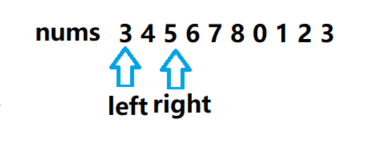
很明显，target 不在 [left,right]。因此直接使用二分法不行。

这是因为该数组在预先未知的某个点上进行了旋转，已不再是一个完全的升序数组。

首先理解以下这个旋转特性。

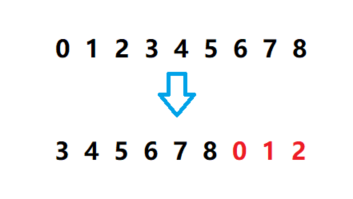
在这里插入图片描述
可以看到，旋转就是将一个有序数组从某两个元素的中间切了一刀，形成了两个有序子数组，然后将第一个有序子数组放到了第二个有序子数组之后。

那么应该如何将这一特性与二分查找结合呢？

这道题中，数组本身不是有序的，进行旋转后只保证了数组的局部是有序的，这还能进行二分查找吗？答案是可以的。

将旋转排序数组均分，一定有一部分的数组是有序的。

拿示例来看，我们从 6 这个位置分开以后数组变成了 [4, 5, 6] 和 [7, 0, 1, 2] 两个部分，其中左边 [4, 5, 6] 这个部分的数组是有序的，其他也是如此。

这启示我们可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的，并根据有序的那个部分确定我们该如何改变二分查找的上下界，因为我们能够根据有序的那部分判断出 target 在不在这个部分。

如果 [l, mid-1] 是有序数组，且 target 大小满足 [nums[l],nums[mid])，则将搜索范围缩小至 [l, mid-1]，否则在 [mid+1, r] 中寻找。
如果 [mid, r] 是有序数组，且 target 大小满足 (nums[mid],nums[r]]，则将搜索范围缩小至 [mid+1, r]，否则在 [l, mid-1] 中寻找。

也就是说，将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。

此时有序部分用二分法查找。无序部分再一分为二，其中一个一定有序，另一个可能有序，可能无序。

就这样循环。

复杂度分析

时间复杂度：O(logn)，其中 n 为 nums 数组的长度。整个算法时间复杂度即为二分查找的时间复杂度。

空间复杂度：O(1)。我们只需要常数级别的空间存放变量。

5.实现示例

下面以 Golang 为例，给出实现示例。

func search(nums []int, target int) int {
l, r := 0, len(nums)-1
	for l <= r {
		mid := (l + r) / 2
		if nums[mid] == target {
			return mid
		}
		// 左区间是有序的。
		if nums[l] <= nums[mid] {
			// target 在左区间
			if target >= nums[l] && target < nums[mid] {
				r = mid - 1
				continue
			}
			// target 在右区间
			l = mid + 1
			continue
		}
		// 右区间是有序的。
		if nums[mid] <= nums[r] {
			// target 在右区间
			if target > nums[mid] && target <= nums[r] {
				l = mid + 1
				continue
			}
			// target 在左区间
			r = mid - 1
			continue
		}
	}
	return -1
}

运行示例：

package main

import (
	"fmt"
)

func main() {
	fmt.Println(search([]int{4, 5, 6, 7, 0, 1, 2}, 0))
	fmt.Println(search([]int{4, 5, 6, 7, 0, 1, 2}, 3))
	fmt.Println(search([]int{1}, 0))
}