一、线段树概念

  线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。它的主要优势是对于区间求和、区间求最大值、区间修改和单点修改的速度快，时间复杂度能达到$O(logN)$。
  若以常规的方法在数组中进行区间求和等操作，时间复杂度会达到$O(n)$，若操作的次数量非常大，那么就很容易超时。线段树的优势就体现出来了
  线段树的实现基于一维数组，用数组下标 $2\ast k+1$ 的元素代表左儿子，用下标 $2\ast k+2$ 的元素代表右儿子来进行树的模拟

对于本文有不理解的小伙伴，建议看B站的这个视频：线段树

二、线段树模板

1.建树

• 线段树建树的操作跟二叉树的建树操作很类似，都利用递归，构建左儿子和右儿子。
• 任意一个结点 $k$，它的左儿子为第 $2\ast k+1$ 个元素，右儿子为第 $2\ast k+2$ 个元素。本例根结点存储的是左儿子和右儿子的和，可应用于区间求和的场景
• 建树时，需要声明一个新的一维数组来存储树的元素，这个数组的大小一般设为原数组长度的4倍及以上
• static int[] arr = {1,3,5,7,9,11};
  static int[] tree = new int[4 * arr.length];

代码：

	/**
	 * @param node 当前结点
	 * @param l 当前结点对应的区间为l~r
	 * @param r
	 */
	public static void build(int node, int l, int r) {
		if (l == r) {
			tree[node] = arr[l];
			return;
		}
		int mid = (l + r) >> 1;
		int l_child = 2 * node + 1;
		int r_child = 2 * node + 2;
		build(l_child, l, mid);	//构建左儿子
		build(r_child, mid + 1, r);	//构建右儿子
		//子树构建好后，更新父结点元素
		tree[node] = tree[l_child] + tree[r_child];
	}

下面画个图理解建立好的树

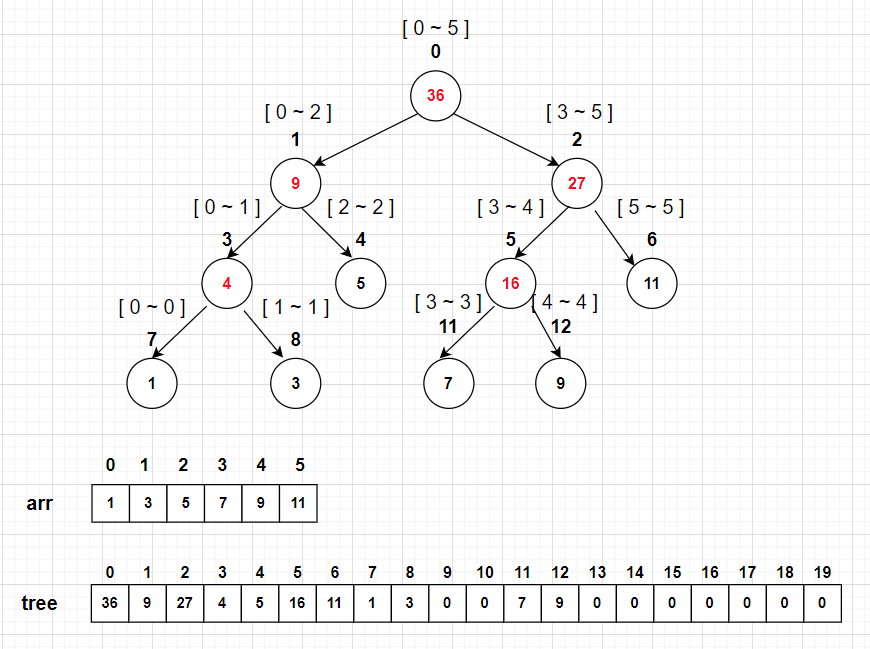
可以看出：

• 叶节点存储原数组的元素，父节点存储左儿子和右儿子的区间和。（对于不同场景，父节点存储元素的意义不同，比如区间求最大值，父节点也可以左儿子和右儿子的区间最大值）
• 线段树采用的是空间换时间，从建树后的tree数组可以看出，有很多空间都没有利用。

2. 单点修改

• 判断修改的点在左子树的区间还是右子树，若在左子树，递归左子树，修改对应的点，反之递归右子树
• 修改后，更新父节点的值

代码：

	/**
	 * @param node 	当前结点
	 * @param l		当前结点对应的区间为l~r
	 * @param r
	 * @param idx	需更新点的下标（原数组下标）
	 * @param val	更新为什么值
	 */
	public static void update(int node, int l, int r, int idx, int val) {
		if (l == r) {	//l=r的时候，表示找到了idx对应的结点
			tree[node] = val;	//更新树的结点
			arr[idx] = val;		//更新原数组的值
			return;
		}
		int mid = (l + r) >> 1;
		int l_child = 2 * node + 1;
		int r_child = 2 * node + 2;
		if (idx <= mid) {
			update(l_child, l, mid, idx, val);
		}else {
			update(r_child, mid + 1, r, idx, val);
		}
		//对应元素更新好后，更新父节点的值
		tree[node] = tree[l_child] + tree[r_child];
	}

例如，更新 4 号元素为 6，更新后的树如下图

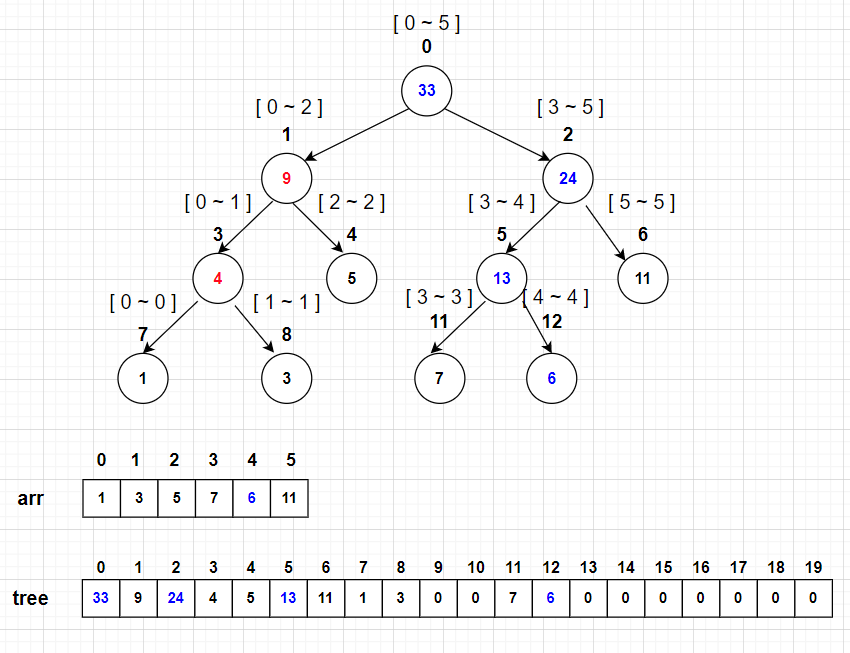
3.区间查询

• 当前结点对应的区间若不在查询的范围内，返回 0
• 查询范围包含了当前结点对应区间的范围，直接返回当前结点的元素

代码：

	/**
	 * @param node	当前结点
	 * @param l		当前结点对应的区间为l~r
	 * @param r
	 * @param start 查询区间的范围为start~end
	 * @param end
	 * @return
	 */
	public static int query(int node, int l, int r, int start, int end) {
		if (start > r || end < l) {	//不在查询的范围
			return 0;
		}
		if (start <= l&& end >= r) {//在查询范围，直接返回
			return tree[node];
		}
		int mid = (l + r) >> 1;
		int l_child = node * 2 + 1;
		int r_child  = node * 2 + 2;
		int l_sum = query(l_child, l, mid, start, end);		//左子树的和
		int r_sum = query(r_child, mid + 1, r, start, end);	//右子树的和
		//返回左子树加右子树的和
		return l_sum + r_sum;
	}

例如查更新后的树的 2~5 号元素的区间和：

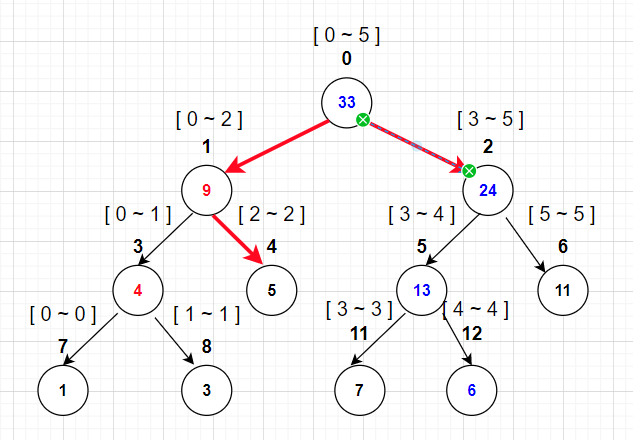
• 1.查询左子树$[0,2]$，再查询到其右子树$[2,2]$，在查询的区间内，直接返回 5
• 2.查询右子树$[3,5]$，在查询的区间内，直接返回 24.
• 3.计算左子树和右子树的和 $5+24=29$

线段树的其他区间求最大值、区间修改的方式，与本文的方法类似，就不再赘述，有兴趣的小伙伴可以自行实现

4.完整代码及测试

public class 线段树 {
	static int[] arr = {1,3,5,7,9,11};
	static int[] tree = new int[4 * arr.length];
	public static void main(String[] args) {
		build(0, 0, arr.length - 1);
		for (int i = 0; i < 4 * arr.length; i++) {
			System.out.print(tree[i] + " ");
		}
		System.out.println();
		update(0, 0, arr.length - 1, 4, 6);
		for (int i = 0; i < 4 * arr.length; i++) {
			System.out.print(tree[i] + " ");
		}
		int s = query(0,0,arr.length - 1, 2 , 5);
		System.out.println("\n" + s);
	}
	/**
	 * @param node 当前结点
	 * @param l l和r表示当前的范围
	 * @param r
	 */
	public static void build(int node, int l, int r) {
		if (l == r) {
			tree[node] = arr[l];
			return;
		}
		int mid = (l + r) >> 1;
		int l_child = 2 * node + 1;
		int r_child = 2 * node + 2;
		build(l_child, l, mid);
		build(r_child, mid + 1, r);
		tree[node] = tree[l_child] + tree[r_child];
	}
	/**
	 * @param node 	当前结点
	 * @param l		当前结点对应的区间为l~r
	 * @param r
	 * @param idx	需更新点的下标（原数组下标）
	 * @param val	更新为什么值
	 */
	public static void update(int node, int l, int r, int idx, int val) {
		if (l == r) {	//l=r的时候，表示找到了idx对应的结点
			tree[node] = val;	//更新树的结点
			arr[idx] = val;		//更新原数组的值
			return;
		}
		int mid = (l + r) >> 1;
		int l_child = 2 * node + 1;
		int r_child = 2 * node + 2;
		if (idx <= mid) {
			update(l_child, l, mid, idx, val);
		}else {
			update(r_child, mid + 1, r, idx, val);
		}
		//更新父节点的值
		tree[node] = tree[l_child] + tree[r_child];
	}
	
	/**
	 * @param node	当前结点
	 * @param l		当前结点对应的区间为l~r
	 * @param r
	 * @param start 查询区间的范围为start~end
	 * @param end
	 * @return
	 */
	public static int query(int node, int l, int r, int start, int end) {
		if (start > r || end < l) {	//不在查询的范围
			return 0;
		}
		if (start <= l&& end >= r) {//在查询范围，直接返回
			return tree[node];
		}
		int mid = (l + r) >> 1;
		int l_child = node * 2 + 1;
		int r_child  = node * 2 + 2;
		int l_sum = query(l_child, l, mid, start, end);		//左子树的和
		int r_sum = query(r_child, mid + 1, r, start, end);	//右子树的和
		//返回左子树加右子树的和
		return l_sum + r_sum;
	}
}

测试截图：