✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，matlab项目合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

更多Matlab仿真内容点击👇

智能优化算法  神经网络预测 雷达通信  无线传感器

信号处理 图像处理 路径规划 元胞自动机 无人机  电力系统

⛄ 内容介绍

旅行商问题是一个经典的NP完全问题,多人旅行商问题的求解则更具挑战性.以往对求解多人旅行商问题的研究局限于以所有成员路径总和最小为优化标准,而对以所有成员路径最大值最小为优化标准的另一类多人旅行商问题却未加注意.文章给出了这两类多人旅行商问题的形式化描述,探讨了利用遗传算法求解这固定的开放式多旅行推销员问题(M-TSP)的基本思想和具体方案,进行了仿真实验验证.仿真实验数据表明,这是一种高效而且适应性强的多入旅行商问题求解方法.

⛄ 部分代码

clc;

clear all;

close all

xy = 100*rand(29,2);%坐标

N = size(xy,1);%城市数量

dmat = xlsread('1.xlsx','Sheet1','B2:AD30');%距离

min_tour = 4;%最小时间限制

pop_size = 200;%种群数量

num_iter = 1000;%迭代次数

n = N - 1; % 减去起点

for salesmen=2:7%旅行商个数循环

    

    % 线路断点选择的初始化

    num_brks = salesmen-1;

    % 初始化种群

    pop_rte = zeros(pop_size,n);          %路径初始化

    pop_brk = zeros(pop_size,num_brks);   % population of breaks

            for k = 1:8 % Generate New Solutions

                tmp_pop_rte(k,:) = best_of_8_rte;

                tmp_pop_brk(k,:) = best_of_8_brk;

                switch k

                    case 2 % Flip

                        tmp_pop_rte(k,I:J) = fliplr(tmp_pop_rte(k,I:J));

                    case 3 % Swap

                        tmp_pop_rte(k,[I J]) = tmp_pop_rte(k,[J I]);

                    case 4 % Slide

                        tmp_pop_rte(k,I:J) = tmp_pop_rte(k,[I+1:J I]);

                    case 5 % Modify Breaks

                        tmp_pop_brk(k,:) = randbreaks(min_tour,n,num_brks,cum_prob);

                    case 6 % Flip, Modify Breaks

                        tmp_pop_rte(k,I:J) = fliplr(tmp_pop_rte(k,I:J));

                        tmp_pop_brk(k,:) = randbreaks(min_tour,n,num_brks,cum_prob);

                    case 7 % Swap, Modify Breaks

                        tmp_pop_rte(k,[I J]) = tmp_pop_rte(k,[J I]);

                        tmp_pop_brk(k,:) = randbreaks(min_tour,n,num_brks,cum_prob);

                    case 8 % Slide, Modify Breaks

                        tmp_pop_rte(k,I:J) = tmp_pop_rte(k,[I+1:J I]);

                        tmp_pop_brk(k,:) = randbreaks(min_tour,n,num_brks,cum_prob);

                    otherwise % Do Nothing

                end

            end

            new_pop_rte(p-7:p,:) = tmp_pop_rte;

            new_pop_brk(p-7:p,:) = tmp_pop_brk;

        end

        pop_rte = new_pop_rte;

        pop_brk = new_pop_brk;

    end

    %     if global_min<100%如果＜200则跳出循环

    

    ds=zeros(s,1);

    flg=0;

    for s = 1:salesmen

        %         disp(['旅行商',num2str(s),'的路径：'])

        

        ds(s) = ds(s) + dmat(1,opt_rte(rng(s,1))); % 计算起点到旅行商第一个城市的距离

        rte = [1 opt_rte(rng(s,1):rng(s,2))];

        for i=1:length(rte)-1

            ds(s) = ds(s) + dmat(rte(i),rte(i+1)); % 计算起点到旅行商第一个城市的距离

        end

        if ds(s)>22

            flg=flg+1;

        end

    end

    if flg==0

        disp(['最少旅行商数量为',num2str(salesmen)]);

        %         disp(['最短路径为：',num2str(min_dist)])

        

        ds=zeros(s,1);

        for s = 1:salesmen

            disp(['旅行商',num2str(s),'的路径：'])

            d(s) = d(s) + dmat(1,opt_rte(rng(s,1))); % 计算起点到旅行商第一个城市的距离

            rte = [1 opt_rte(rng(s,1):rng(s,2))]

            for i=1:length(rte)-1

                ds(s) = ds(s) + dmat(rte(i),rte(i+1)); % 计算起点到旅行商第一个城市的距离

            end

            ds(s)

        end

        break;

    end

    

end

disp('总路程')

disp(sum(ds));

% Plot the Best Route

figure(1);%显示城市分布图

for s = 1:salesmen

    rte = [1 opt_rte(rng(s,1):rng(s,2))];

    plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:));

    title(sprintf('Total Distance = %1.4f, Iteration = %d',min_dist,iter));

    hold on

end

plot(xy(1,1),xy(1,2),'ko');

hold off

% Plots

figure('Name','MTSPOFS_GA | Results','Numbertitle','off');%距离矩阵，没啥用

subplot(2,2,1);

plot(xy(:,1),xy(:,2),'k.');

title('City Locations');

subplot(2,2,2);

imagesc(dmat([1 opt_rte],[1 opt_rte]));

title('Distance Matrix');

subplot(2,2,3);%显示路径规划图

rng = [[1 opt_brk+1];[opt_brk n]]';

for s = 1:salesmen

    rte = [1 opt_rte(rng(s,1):rng(s,2))];

    plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:));

    title(sprintf('Total Distance = %1.4f',min_dist));

    hold on;

end

plot(xy(1,1),xy(1,2),'ko');

subplot(2,2,4);%显示迭代图

plot(dist_history,'b','LineWidth',2);

title('Best Solution History');

set(gca,'XLim',[0 num_iter+1],'YLim',[0 200]);

% Generate Random Set of Break Points

⛄ 运行结果

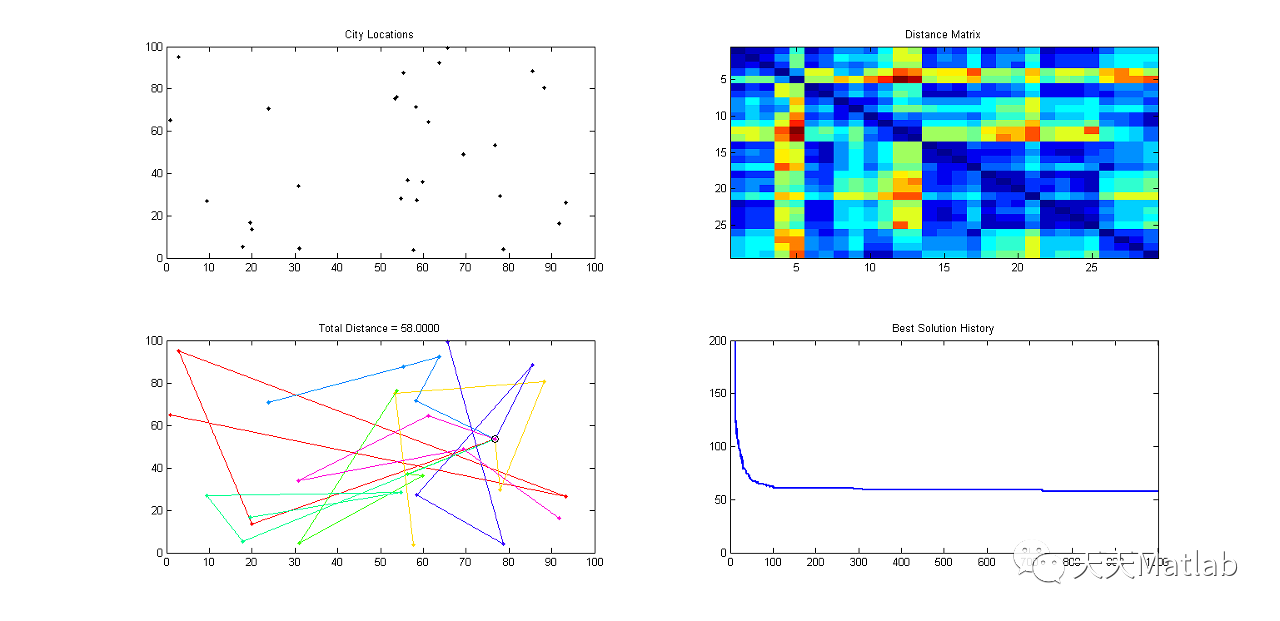
⛄ 参考文献

[2]温清芳. 遗传算法求解TSP问题的MATLAB实现[J]. 秦关学院学报, 2007, 28(6):5.

⛄ Matlab代码关注

❤️部分理论引用网络文献，若有侵权联系博主删除

❤️ 关注我领取海量matlab电子书和数学建模资料