A Swift and Brutal Introduction to Linear Algebra

Garphics’ Dependencies(图形学的依赖)

Basic mathematics(基础的数学)

• Linear alrebra, calculus, statistics

Basic physics(基础的物理)

• Optics, Mechanics

Misc(杂项)

• Signal processing
• Numerical analysis

And a bit of asethetics(以及一点美学)

Vectors(向量)

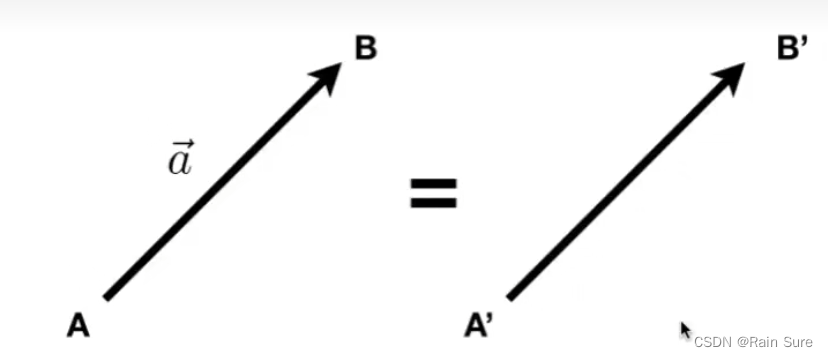
• 通常写成$\vec{a}$或者加粗的a;
• 或者使用起点或者重点来表示：$\overrightarrow{AB}=B-A$;
• 向量最重要的两个属性：长度和方向；
• 没有绝对的开始的位置；

Vector Normalization(向量归一化)

• 向量的大小通常写为$||\vec{a}||$
• 单位向量
  • 长度为1的向量
  • 计算一个向量的单位向量：$\hat{a}=\vec{a}/||\vec{a}||$
  • 用于表示方向

Vector Addition(向量求和)

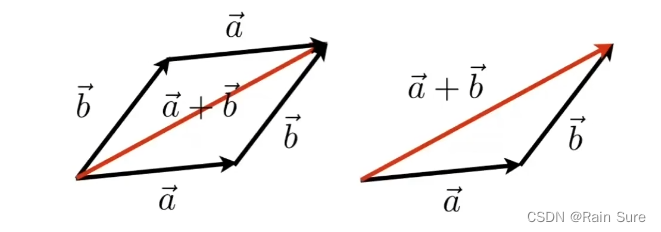
• 几何意义：平行四边形法则 && 三角形法则
• 代数意义：简单的坐标相加

Vector Multiplication(向量乘法)

• Dot product(点乘)

  1. $\vec{a}\cdot \vec{b}=||\vec{a}||||\vec{b}||cos\theta$
  2. $cos\theta =\frac{\vec{a}\cdot \vec{b}}{||\vec{a}||||\vec{b}||}$
  3. 对于单位向量：$cos\theta =\hat{a}\cdot \hat{b}$
  4. 性质：
     • $\vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{a}$
     • $\vec{a}\cdot (\vec{b}+\vec{c})=\vec{a}\cdot \vec{b}+\vec{a}\cdot \vec{c}$
     • $(k\vec{a})\cdot \vec{b}=\vec{a}\cdot (k\vec{b})=k(\vec{a}\cdot \vec{b})$
  5. 分别相乘，然后相加
     • In 2D:
       $\vec{a}\cdot \vec{b}=\left(\begin{array}{l}{x}_a\\ y_a\end{array}\right)\cdot \left(\begin{array}{l}{x}_b\\ y_b\end{array}\right)=x_a{x}_b+y_a{y}_b$
     • In 3D:
       $\vec{a}\cdot \vec{b}=\left(\begin{array}{l}{x}_a\\ y_a\\ z_a\end{array}\right)\cdot \left(\begin{array}{l}{x}_b\\ y_b\\ z_b\end{array}\right)=x_a{x}_b+y_a{y}_b+z_a{z}_b$
     6. 作用
        • 计算两个向量的夹角
        • 计算一个向量到另一个向量的投影
        • 测量两个方向离的有多近
        • 分解一个向量，垂直与平行
        • 决定方向朝前or朝后

• Cross product(叉乘)
  

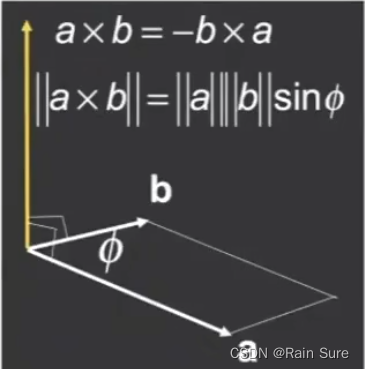
  1. 两个向量叉乘的结果与两个原始向量正交。
  2. 方向由右手定则决定。
  3. 在构建坐标系时非常有用。
  4. 性质：
     • $\vec{x}\times \vec{y}=+\vec{z}$
     • $\vec{y}\times \vec{x}=-\vec{z}$
     • $\vec{y}\times \vec{z}=+\vec{x}$
     • $\vec{z}\times \vec{y}=-\vec{x}$
     • $\vec{z}\times \vec{x}=+\vec{y}$
     • $\vec{x}\times \vec{z}=-\vec{y}$
     • $\vec{a}\times \vec{b}=-\vec{b}\times \vec{a}$
     • $\vec{a}\times \vec{a}=\vec{0}$
     • $\vec{a}\times (\vec{b}+\vec{c})=\vec{a}\times \vec{b}+\vec{a}\times \vec{c}$
     • $\vec{a}\times (k\vec{b})=k(\vec{a}\times \vec{b})$
  5. 向量叉乘的公式：
     • $\vec{a}\times \vec{b}=\left(\begin{array}{l}{y}_a{z}_b-y_b{z}_a\\ z_a{x}_b-x_a{z}_b\\ x_a{y}_b-y_a{x}_b\end{array}\right)$
     • 也可以写成矩阵乘法的形式：
       
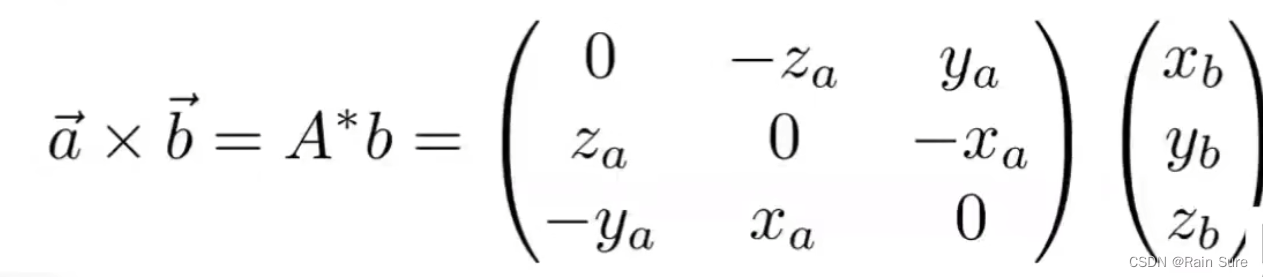
  6. 作用：
     • 判断左右
     • 判断在里面还是在外面

• 定义坐标系

  1. 对于表示点、位置很重要
  2. 要求：单位向量、互相垂直(点乘为0，且叉乘结果为另外一轴)
  3. 可以将任意一个向量分解到三个轴上去，各个轴的投影可以利用点积计算。

Matrices(矩阵)

在图形学中，矩阵常用于表示变换：移动，旋转、缩放、错切等。

矩阵乘法不满足交换律——$AB\ne BA$

满足结合律和分配律：

• $(AB)C=A(BC)$
• $A(B+C)=AB+AC$
• $(A+B)C=AC+BC$

矩阵的转置：

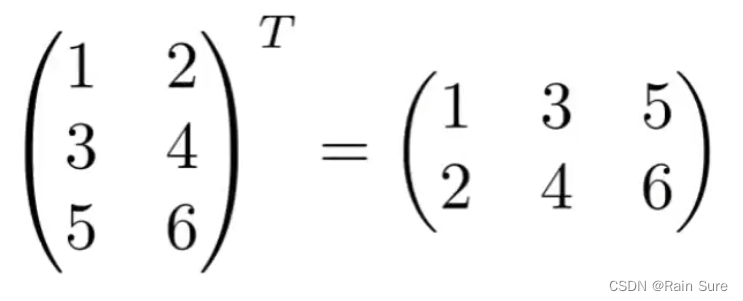
转置的性质：
$(AB{)}^T=B^T{A}^T$

单位矩阵和逆矩阵：

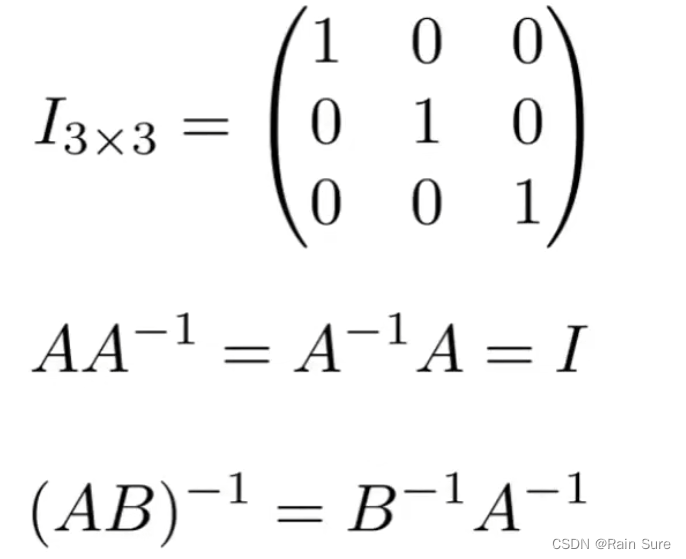
参考资源

GAMES101 Lecture 02 Review of Linear Algebra