Opencv的getRotationMatrix2D函数底层解析

news2024/11/16 21:21:37

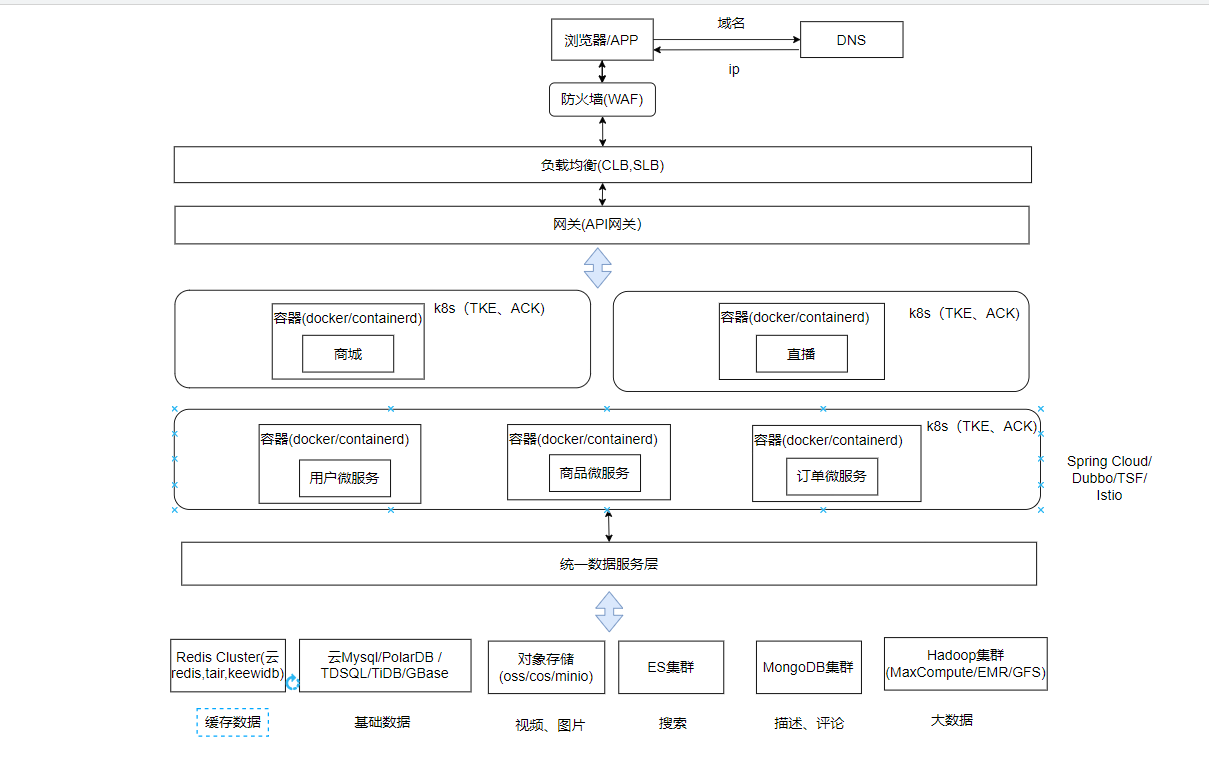
源码

cv::Mat cv::getRotationMatrix2D( Point2f center, double angle, double scale )
{
    angle *= CV_PI/180;
    double alpha = cos(angle)*scale;
    double beta = sin(angle)*scale;
 
    Mat M(2, 3, CV_64F);
    double* m = M.ptr<double>();
 
    m[0] = alpha;
    m[1] = beta;
    m[2] = (1-alpha)*center.x - beta*center.y;
    m[3] = -beta;
    m[4] = alpha;
    m[5] = beta*center.x + (1-alpha)*center.y;
 
    return M;
}

推导

1、有图有真相

为什么这样画图，值得注意的是，计算机中图像的横坐标是向右增加，纵坐标是向下增加！！！

2、任务描述

其中角DAB=α，角CAB=θ

AD与横坐标轴平行，AE与纵坐标轴平行，现在需要沿着A点（centerX,centerY）==>>简写（cx,cy）作为旋转中心

将B点旋转θ角度后到达C点，假设C点坐标为(x',y')，求解x',y'和x,y,θ,cx,cy的数学关系

3、开始计算

AC由AB旋转得到，故其长度相等，令AC=AB=L

于是由三角函数知识

x'=cx+L*cos(α-θ)=cx+L*(cos(α)*cos(θ)+sin(α)*sin(θ)) 1式

y'=cy+L*sin(α-θ)=cy+L*(sin(a)*cos(θ)-sin(θ)*cos(a)) 2式

cos(α)=(x-cx)/L 3式

sin(a)=(y-cy)/L 4式

把3式，4式分别代入1式和2式，可以消去α和L。得到

x'=cx+(x-cx)*cos(θ)+(y-cy)*sin(θ)=x*cos(θ)+y*sin(θ)+cx*(1-cos(θ))-cy*sin(θ)

y'=cy+(y-cy)*cos(θ)-(x-cx)*sin(θ)=x*(-sin(θ))+y*cos(θ)+cy*(1-cos(θ))+cx*sin(θ)

提取出矩阵就是

[

[cos(θ),sin(θ),cx*(1-cos(θ))-cy*sin(θ)],

[-sin(θ),cos(θ),cy*(1-cos(θ))+cx*sin(θ)]

]

验证

实践是检验真理的唯一标准

上Python代码

import numpy as np
import cv2 as cv
import math

cx = 250
cy = 250
angle = 45
scale = 1.0

opencv_M = cv.getRotationMatrix2D((cx, cy), angle, scale)
print(f"opencv_M=\n{opencv_M}")

print("=================================")

cos_angle = math.cos(angle / 180.0 * math.pi)
sin_angle = math.sin(angle / 180.0 * math.pi)
self_M = np.array([
    [cos_angle, sin_angle, cx * (1 - cos_angle) - cy * sin_angle],
    [-sin_angle, cos_angle, cy * (1 - cos_angle) + cx * sin_angle]
])
print(f"self_M=\n{self_M}")

旋转中心(cx,cy)=(250,250)

旋转角度θ=45°

不进行缩放操作scale=1.0

运行结果