1. 概念

回溯算法实际上一个类似枚举的深度优先搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回（也就是递归返回），尝试别的路径。

回溯的处理思想，有点类似枚举（列出所有的情况）搜索。我们枚举所有的解，找到满足期望的解。为了有规律地枚举所有可能的解，避免遗漏和重复，我们把问题求解的过程分为多个阶段。每个阶段，我们都会面对一个岔路口，我们先随意选一条路走，当发现这条路走不通的时候（不符合期望的解），就回退到上一个岔路口，另选一种走法继续走。

2. 经典问题

2.1 问题说明

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
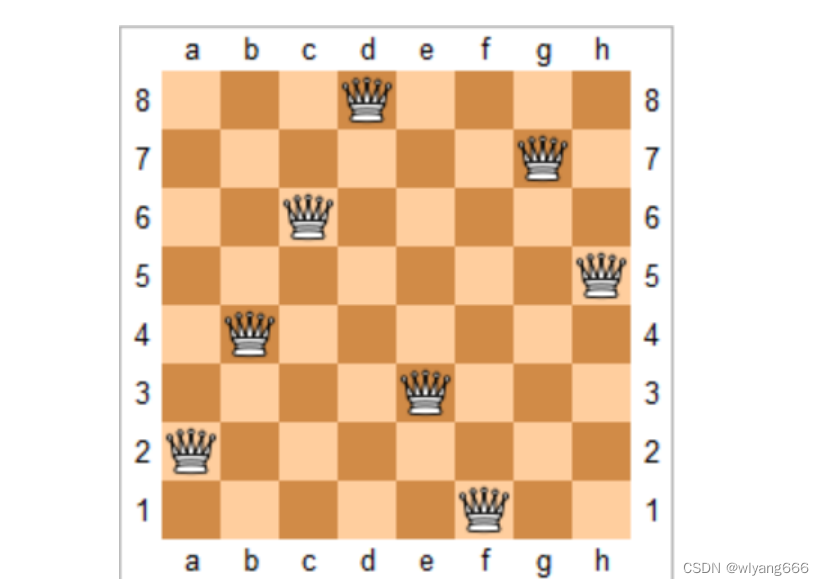
在这里插入图片描述
我们把这个问题划分成 8 个阶段，依次将 8 个棋子放到第一行、第二行、第三行……第八行。在放置的过程中，我们不停地检查当前放法，是否满足要求。如果满足，则跳到下一行继续放置棋子；如果不满足，那就再换一种放法，继续尝试。

2.2 代码验证

package org.wanlong.algorithm;

/**
 * @author wanlong
 * @version 1.0
 * @description:
 * @date 2023/6/16 15:54
 */
public class NQueens {

    //皇后数
    static int QUEENS = 8;
    //下标表示行,值表示queen存储在哪一列
    int[] result = new int[QUEENS];

    /**
     * 在每行放置Queen
     *
     * @param row
     */
    public void setQueens(int row) {
        //递归中断
        if (row == QUEENS) {
            printQueens();
            return;
        }
        //在每行依次放置列 没有合适的则回到上一层
        for (int col = 0; col < QUEENS; col++) {
            if (isOk(row, col)) {
                //设置列
                result[row] = col;
                //开始下一行
                setQueens(row + 1);
            }
        }
    }

    /**
     * 打印输出
     */
    private void printQueens() {
        for (int i = 0; i < QUEENS; i++) {
            for (int j = 0; j < QUEENS; j++) {
                if (result[i] == j) {
                    System.out.print("Q| ");
                } else {
                    System.out.print("*| ");
                }
            }
            System.out.println();
        }
        System.out.println("-----------------------");
    }

    /**
     * 判断是否可以放置
     *
     * @param row 行
     * @param col 列
     * @return
     */
    private boolean isOk(int row, int col) {
        int leftup = col - 1;
        int rightup = col + 1;
        // 逐行往上考察每一行
        for (int i = row - 1; i >= 0; i--) {
            //列上存在queen
            if (result[i] == col)
                return false;
            //左上对角线存在queen
            if (leftup >= 0) {
                if (result[i] == leftup)
                    return false;
            }
            //右下对角线存在queen
            if (rightup < QUEENS) {
                if (result[i] == rightup)
                    return false;
            }
            leftup--;
            rightup++;
        }
        return true;
    }

    public static void main(String[] args) {
        NQueens queens = new NQueens();
        queens.setQueens(0);
    }
}