目录
搜索二叉树概念
代码
二叉搜索树的插入
二叉搜索树的查找
二叉搜索树的删除（非常重要）
a、b、c情况：删除14
d情况
打印结点中序遍历
整体代码：（有R开头的就是递归写法，逻辑一样）
搜索二叉树概念
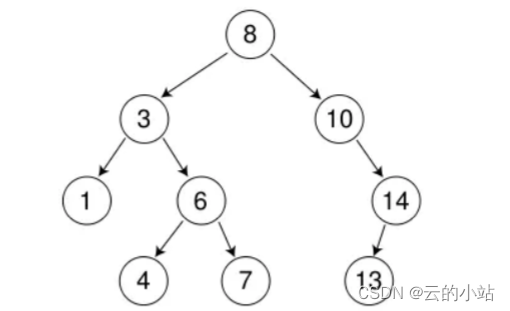
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:、
| 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值 |
| 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值 |
| 它的左右子树也分别为二叉搜索树 |
错误例子：
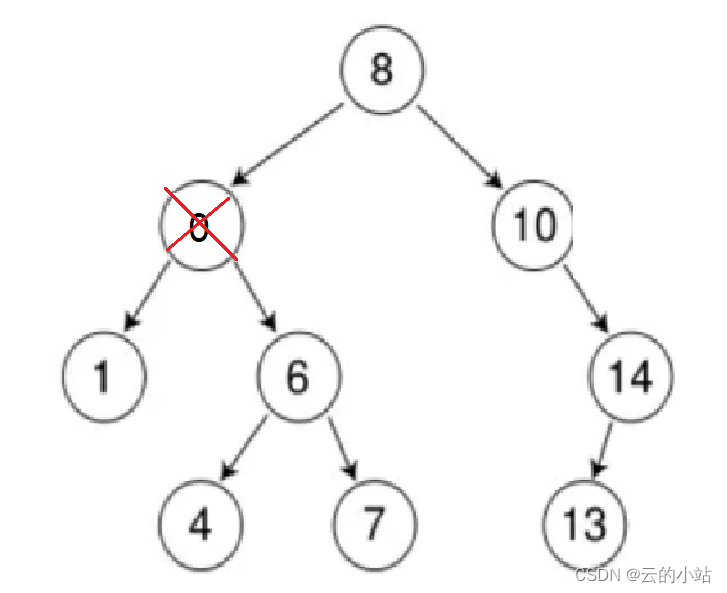
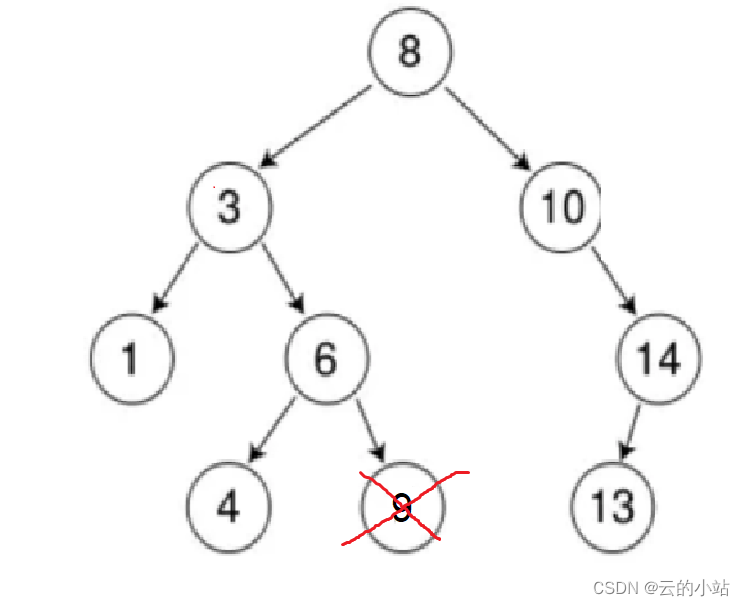
1、不是搜索树，数据为0不应该在这个位置，应为它比他的左子树还要小
2、不是搜索树，数据9虽然比自己的父亲6大位置合适，但是他的祖父8的左子树
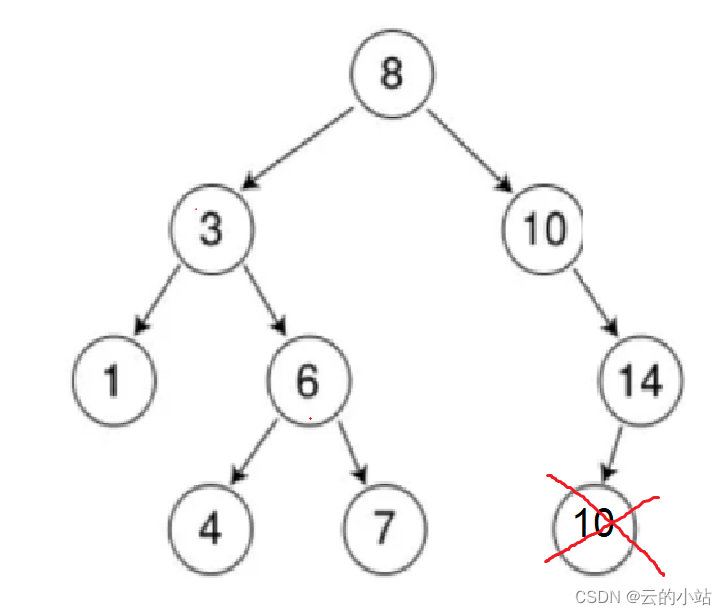
3、不是搜索树，数据10虽然比自己的父亲14小位置合适，但是祖父10相等，但是搜索树里面的key值必须唯一值。
代码
二叉搜索树的插入
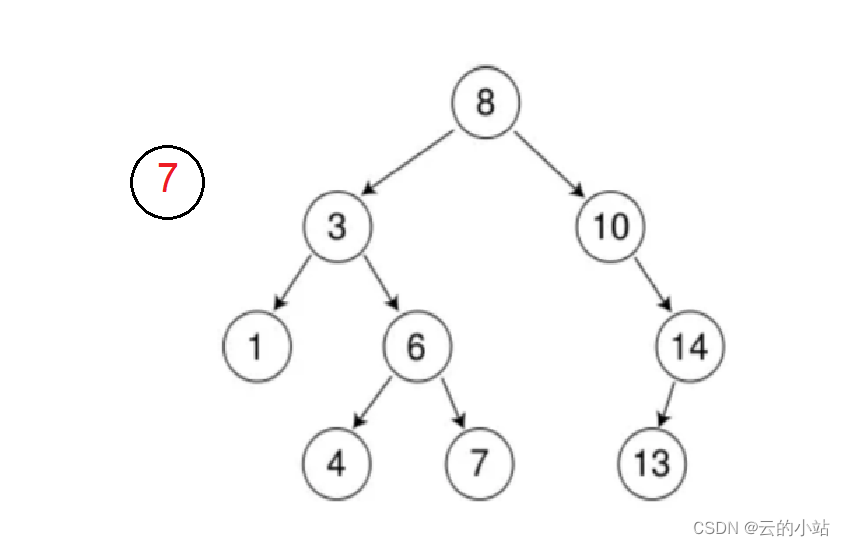
二叉树的链接一定在叶子结点上，现在我们要插入7这个数据，从头开始比较寻找数据，使用2个指针，一个指针保存寻找路径。一个指针（cur）保存寻找路径，一个保存(prev)父节点。
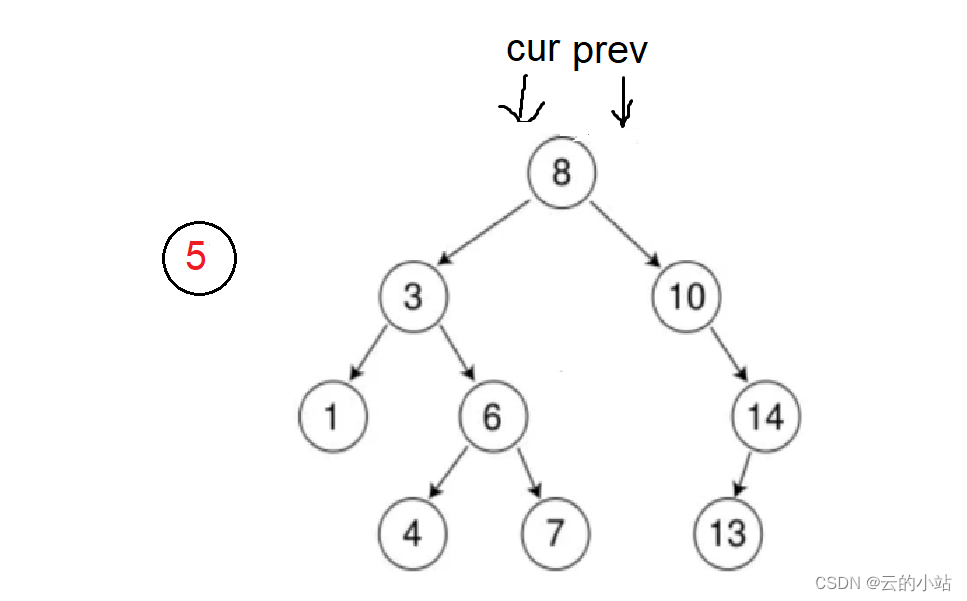
8>5 ,prev=cur,cur=cur->left
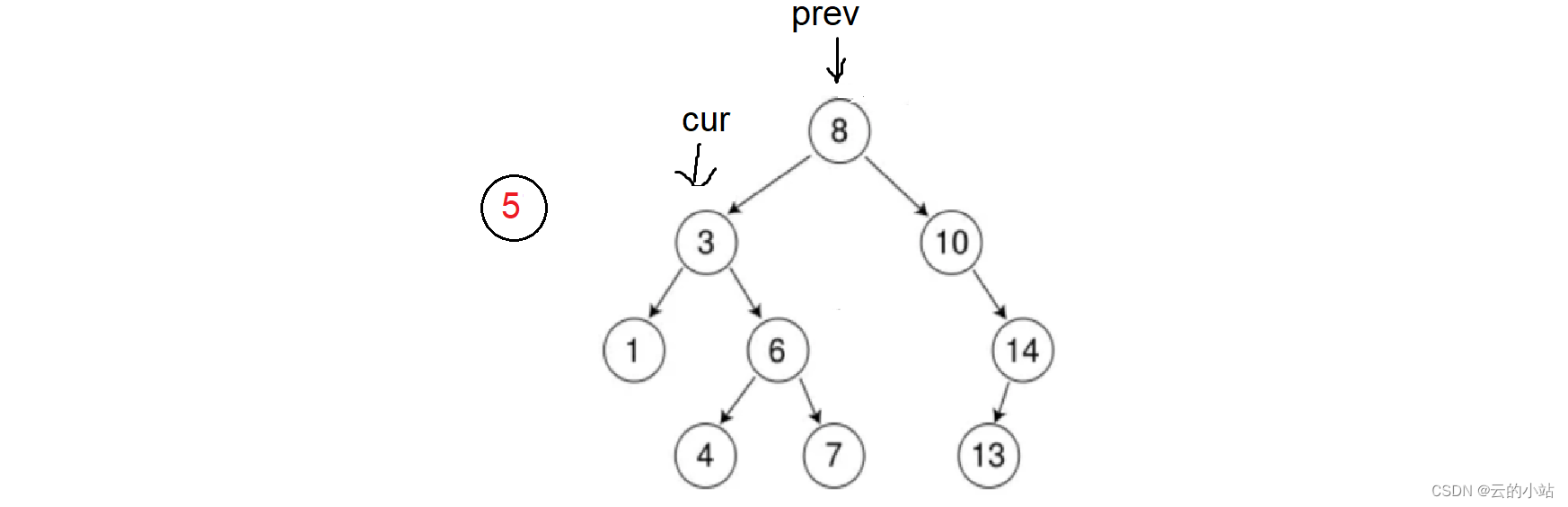
3<5,prev=cur,cur=cur->right
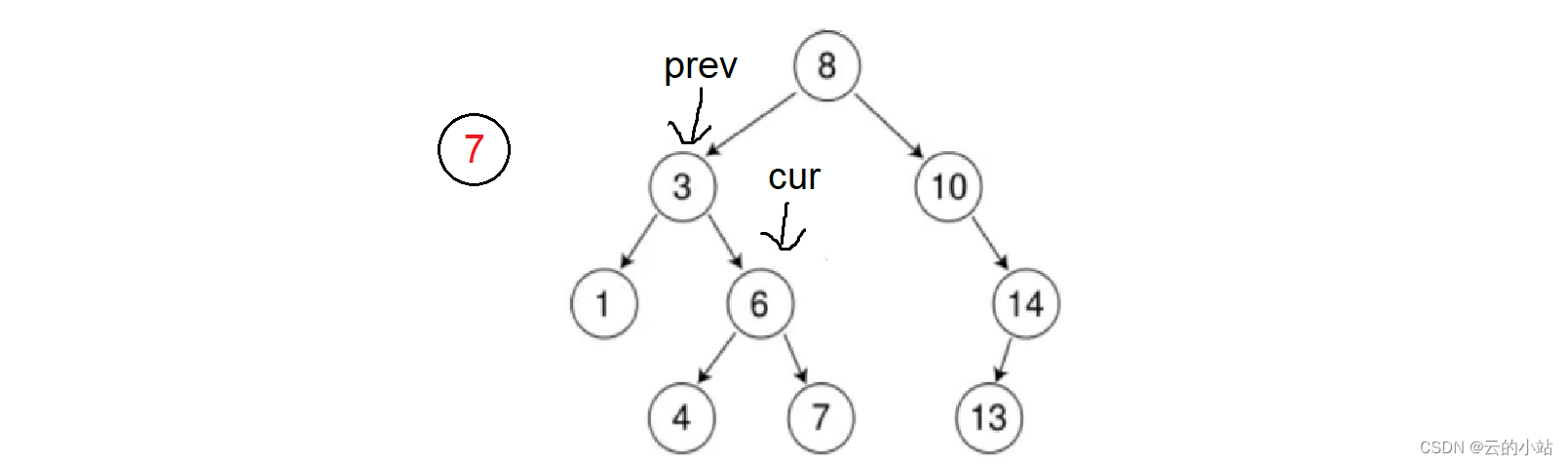
6>5,prev=cur,cur=cur->left
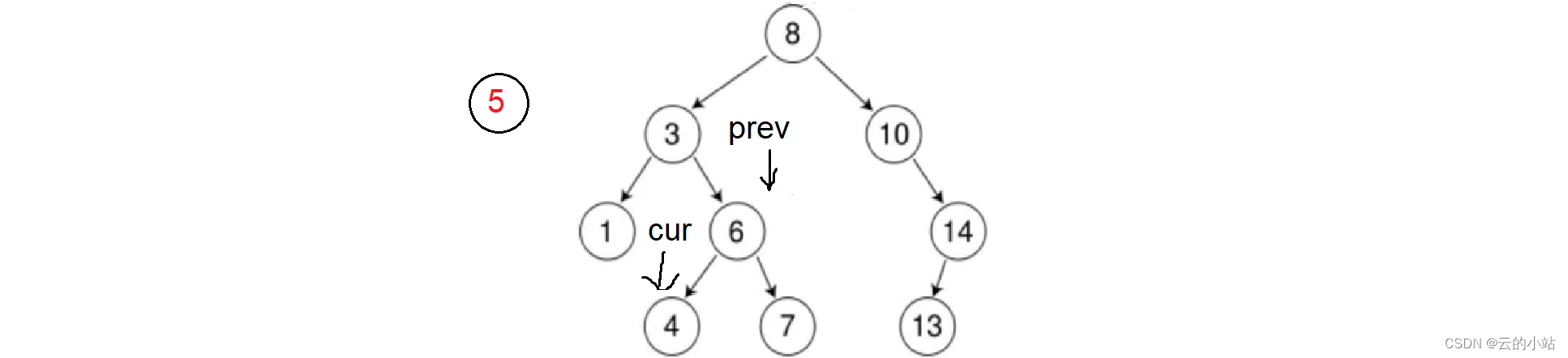
4<5,prev=cur,cur=cur->right
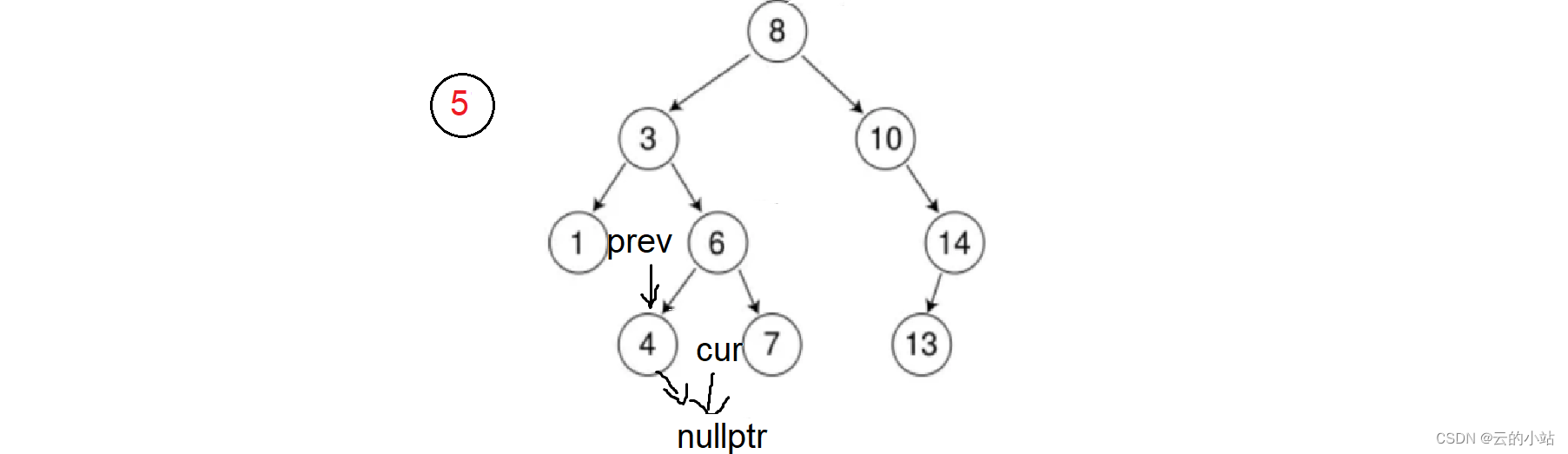
当cur到空，开始链接新结点，new一个node结点，然后cur指向新结点。
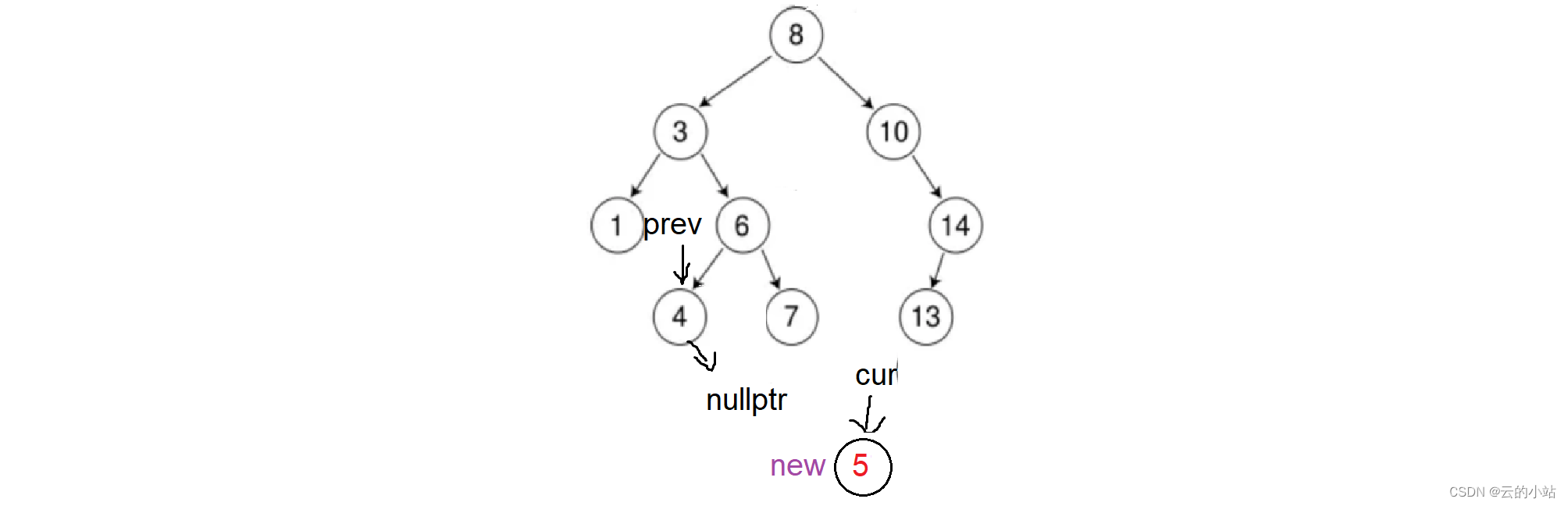
让prev的空子树指向cur。这里有个俩问题我们并不知道链接到prev的左子树还是右子树，如果用空子树判断，若是左右子树都为空，就无法判断
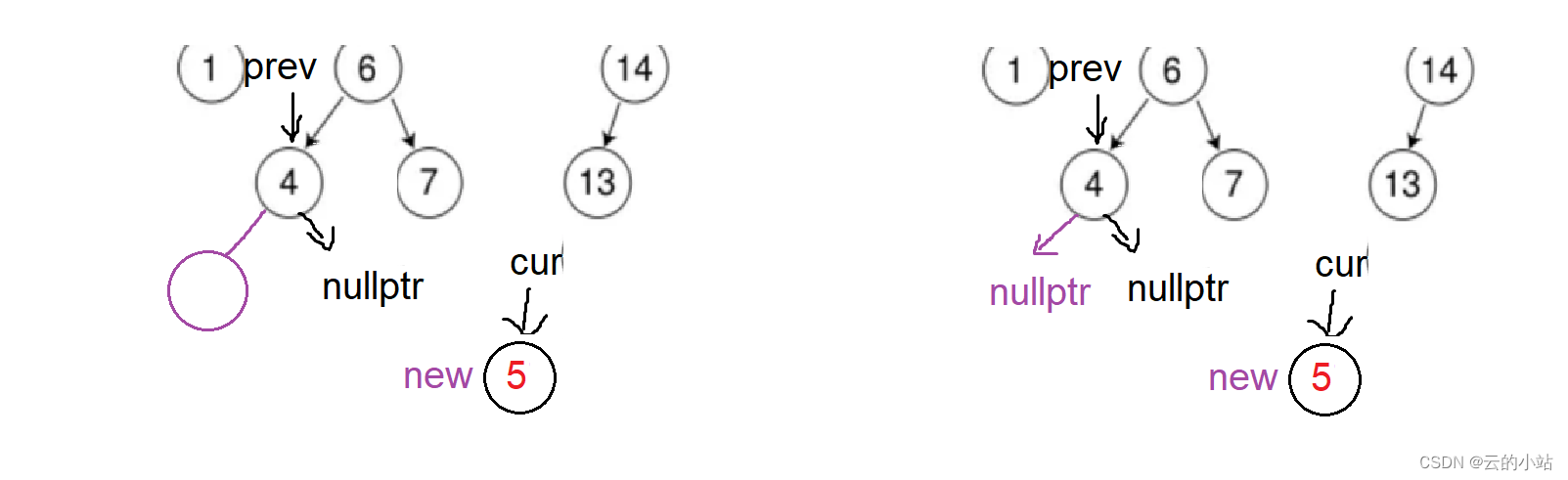
所以我们唯一的方式就是比较prev与cur现在保存的key。
perv->key<cur->key;perv->right=cur;
perv->key>cur->key;perv->left=cur;
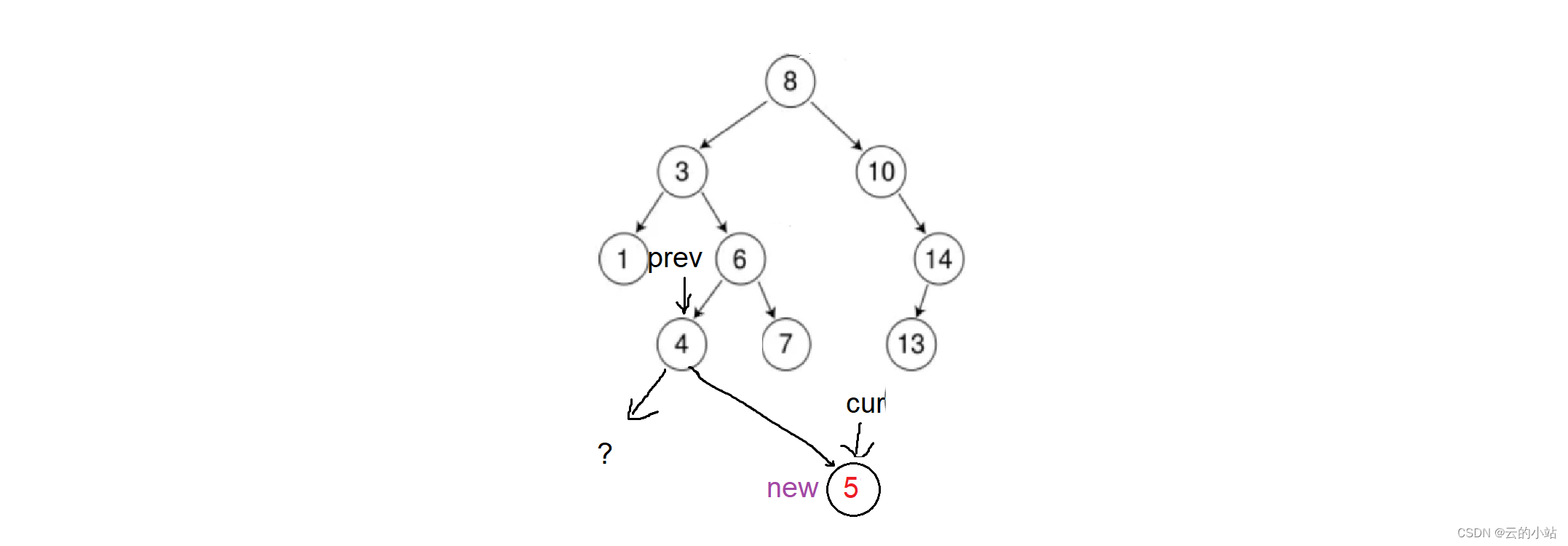
因为上一层的循环查找也这个比较条件到了空子树，所以再一次比较数据就知道应该链接的子树了。
二叉搜索树的查找
a、从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。
b、最多查找高度次，走到到空，还没找到，这个值不存在。
二叉搜索树的删除（非常重要）
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
无孩子和只有一个孩子可以合并，应为删除后我们可以父节点指向该结点的空子树的另一端。
a、b、c情况：删除14
情况一：条件->cur在prev右子树
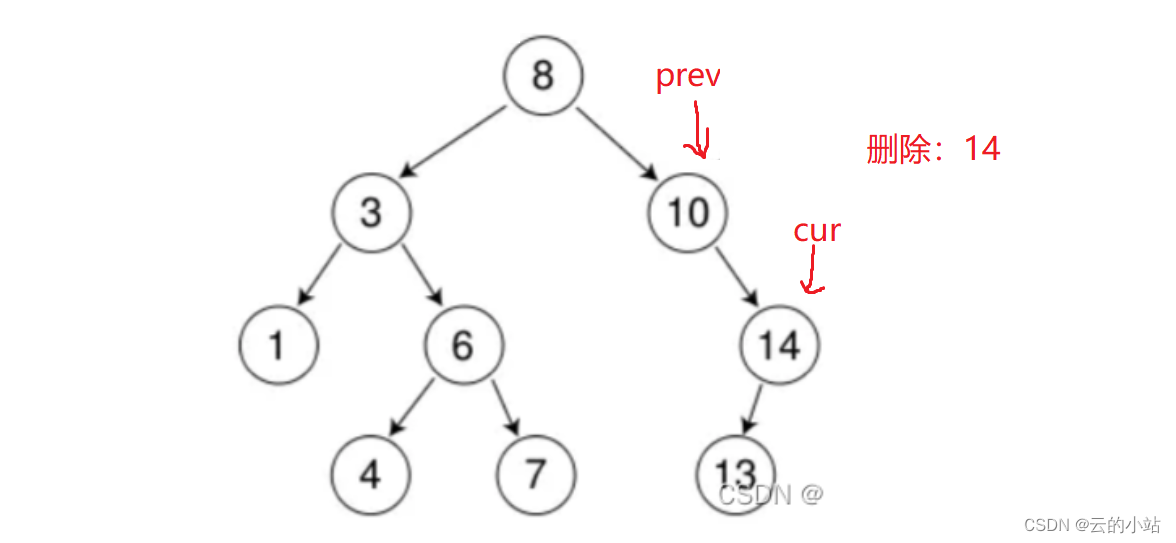
当我们删除14时候，需要判断14的左右子树哪个为空（都为空也行）。应为我们需要将cur的非空子树链接（也可以是空）。
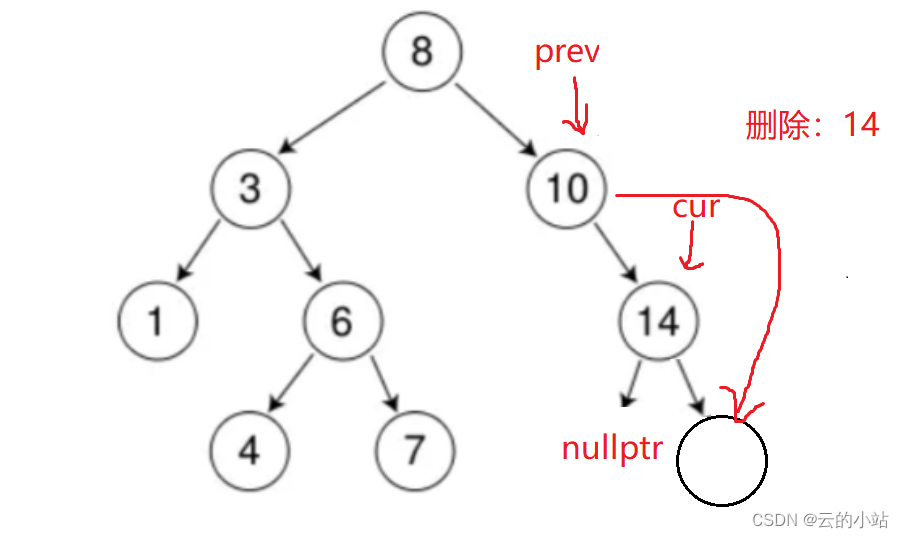cur结点左子树为空,prev->right指向cur->right
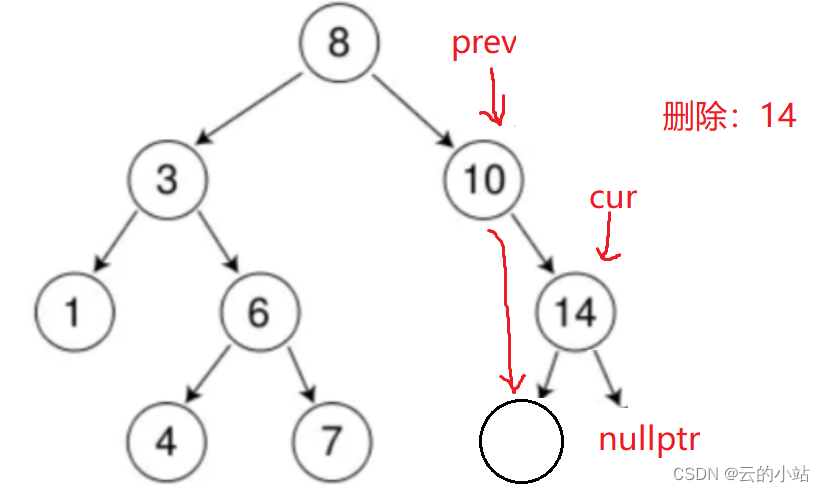cur结点右子树为空,prev->left指向cur->left
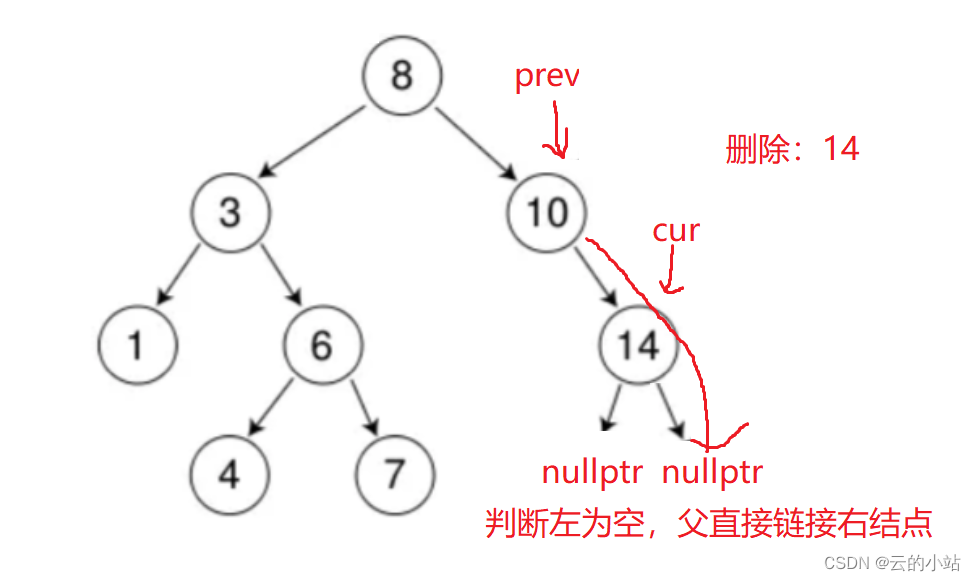cur结点左子树为空,prev->right直接指向cur->right，不论是否为空（解决a情况）。
但是我们的前提有个条件：cur在prev右子树，所以我们还得判断一下cur在prev的哪一边。
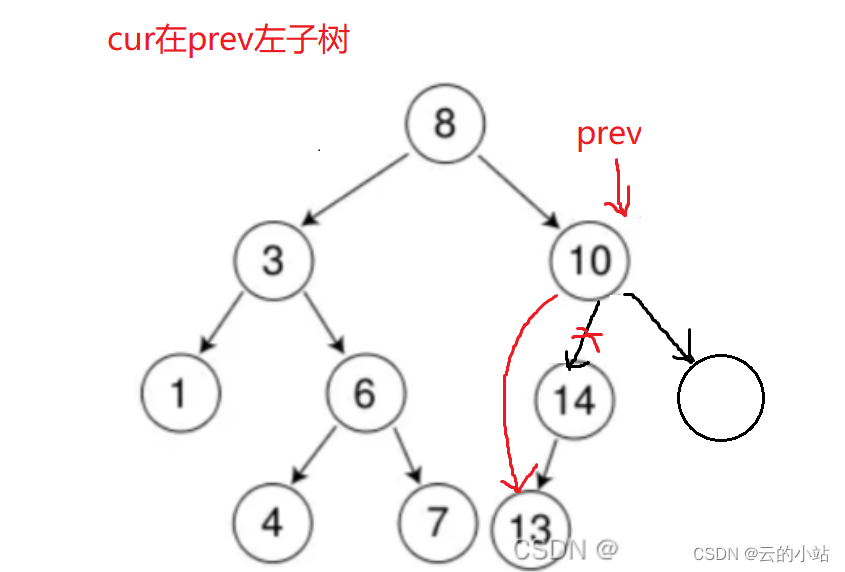
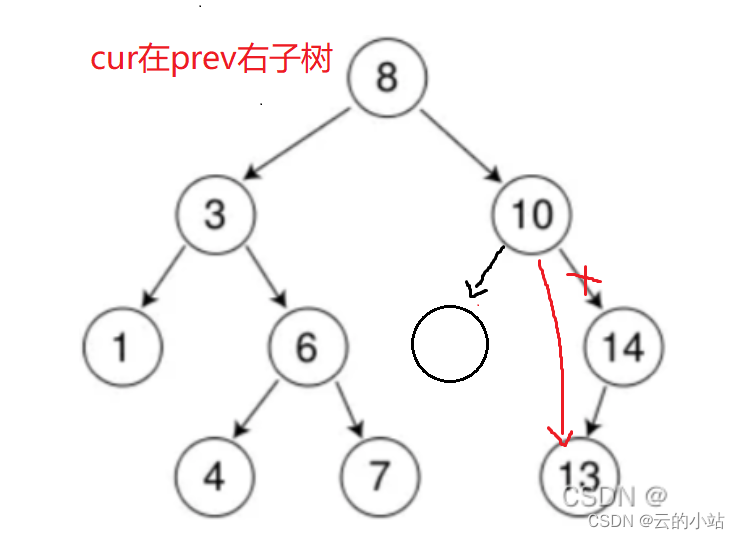
我们的寻找结点可是左右左右的寻找。
但是还有一种情况还没判断，就是cur==root（根节点）。
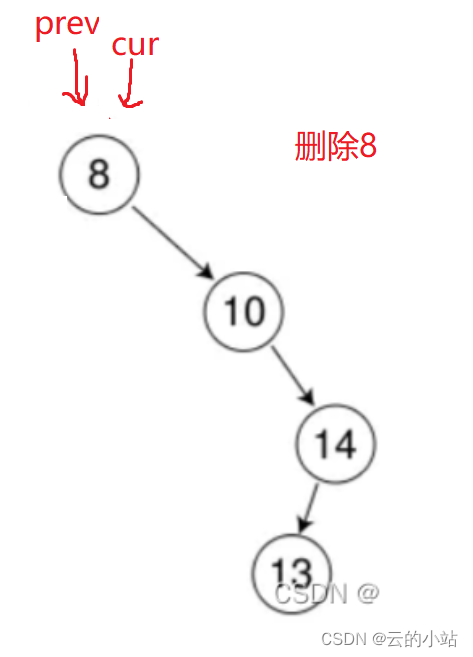
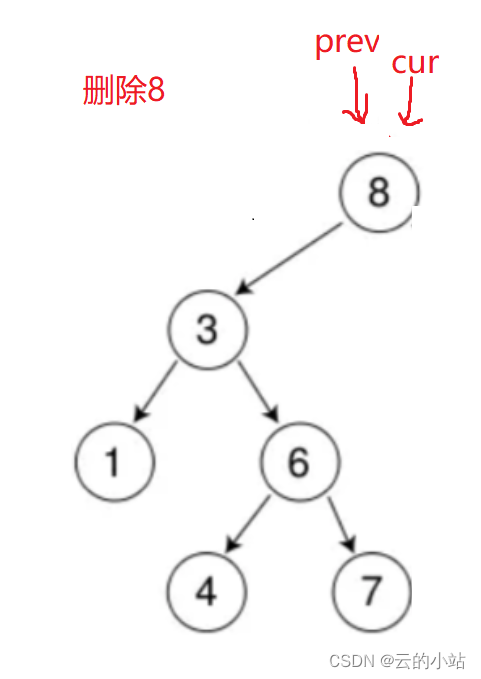
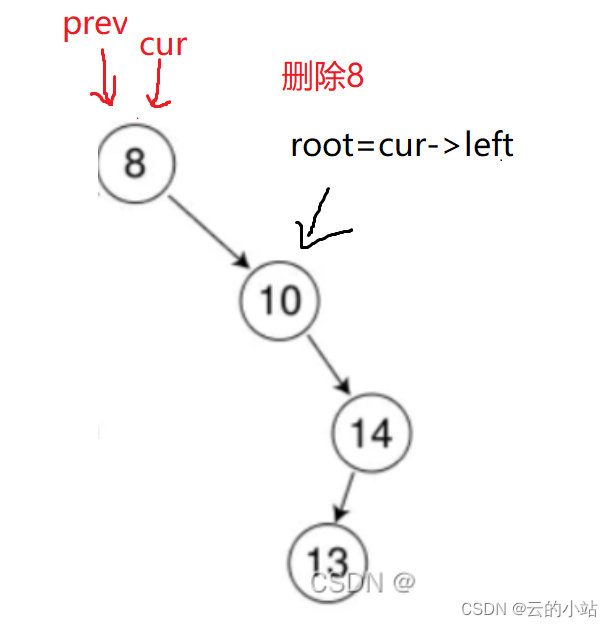
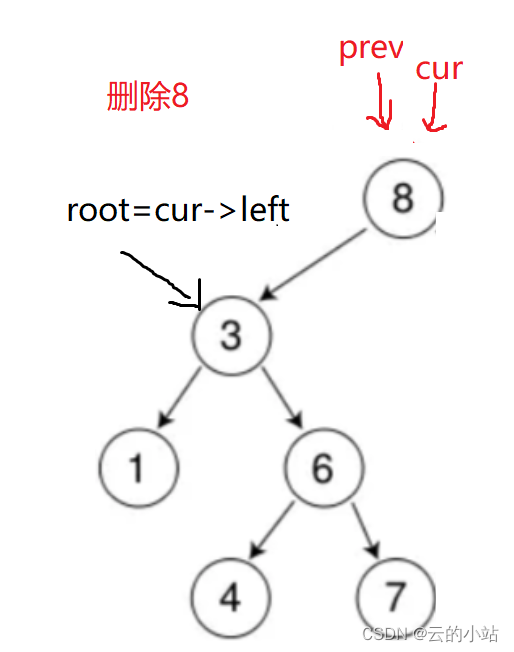
可以在cur判断左右空子树的if-else里做if判断，如果为cur==root让root=cur->非空子树（也可以空）。
//判断左右子树是否为空，只要有一个为空就会进入第一种删除：普通删除结点
//+++++++++++++++++++++++++++++第一种开始++++++++++++++++++++++++++++++++
//cur的左树为空
if (cur->_left == nullptr)
{
//判断是否为根结点
if (cur == _root)
{
_root = cur->_right;
}
else
{
//判断是在cur在prev左右那一颗子树
if (prev->_left == cur)
{
prev->_left = cur->_right;
}
else
{
prev->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
}
//cur的左树为空
else if (cur->_right == nullptr)
{
//......
}
//+++++++++++++++++++++++++++++第一种结束++++++++++++++++++++++++++++++++
d情况
当我们要删除一个拥有双非空子树结点时，就不可以普通删除了，极可能破坏搜索树结构
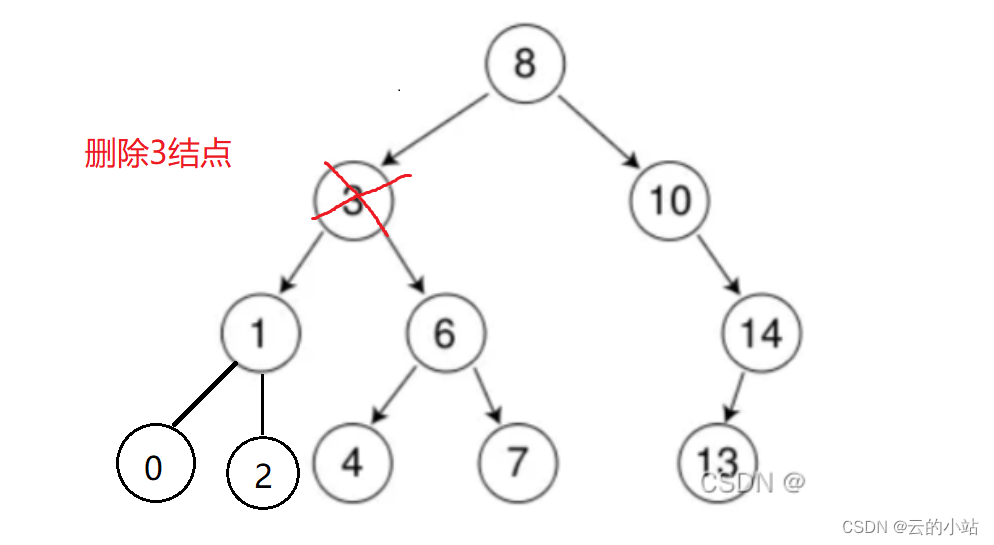
单纯删除3结点，我们的父节点根本无法判断如何链接被这被删除的结点下的子树，链接6就要放弃1，链接1就要放弃6.这是我们不愿意看到的结果。所以当被删除的结点左右树都为非空时，我们需要换一个方法删除3结点--->替换法
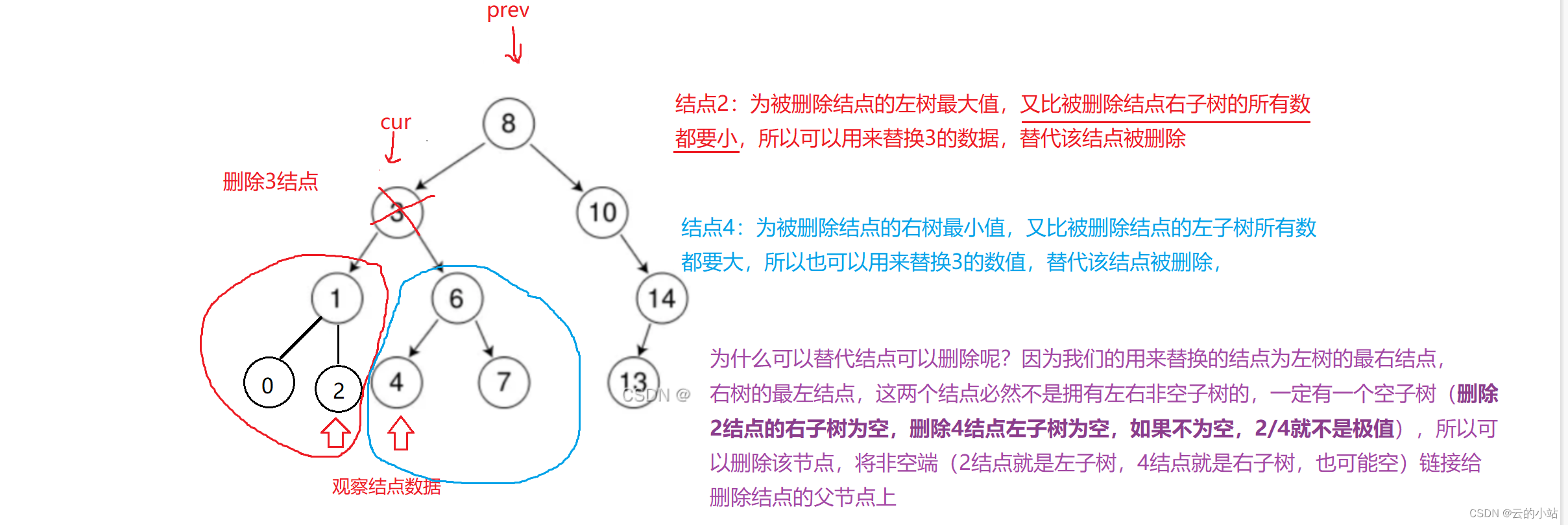
我们来删除3结点来演示，我们寻找3结点右数的极小值做替换删除演示。
首先寻找cur删除结点右子树蓝圈中的最小值，定义2个结点寻找极值，一个结点保存极值结点，一个保存极值的父节点。初始值：fdele=cur，dele=cur->right
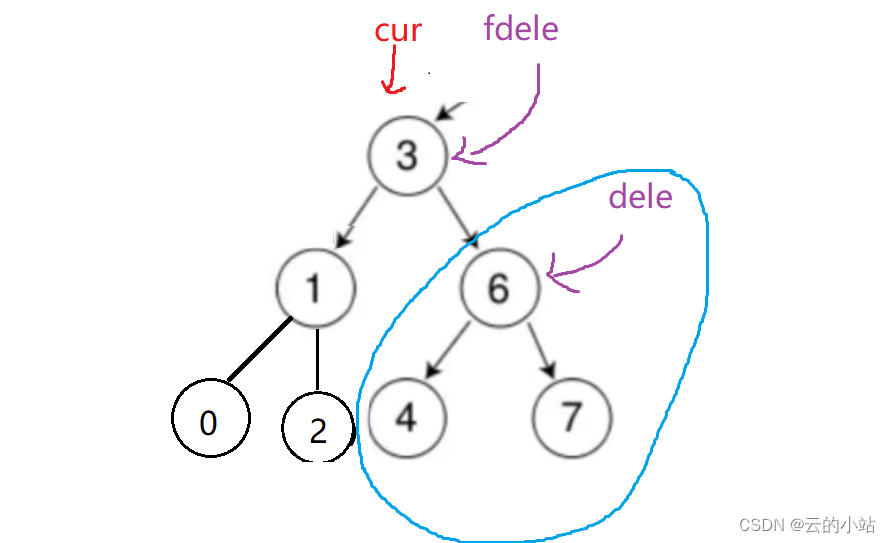
循环寻找代码为：
dele=cur->right;
fdele=cur;
whlie(dele->left!=nullptr)
{
fdele=dele;
dele=dele->left;
}一旦循环结束就意味着到了cur右子树的最左结点来到了极值。
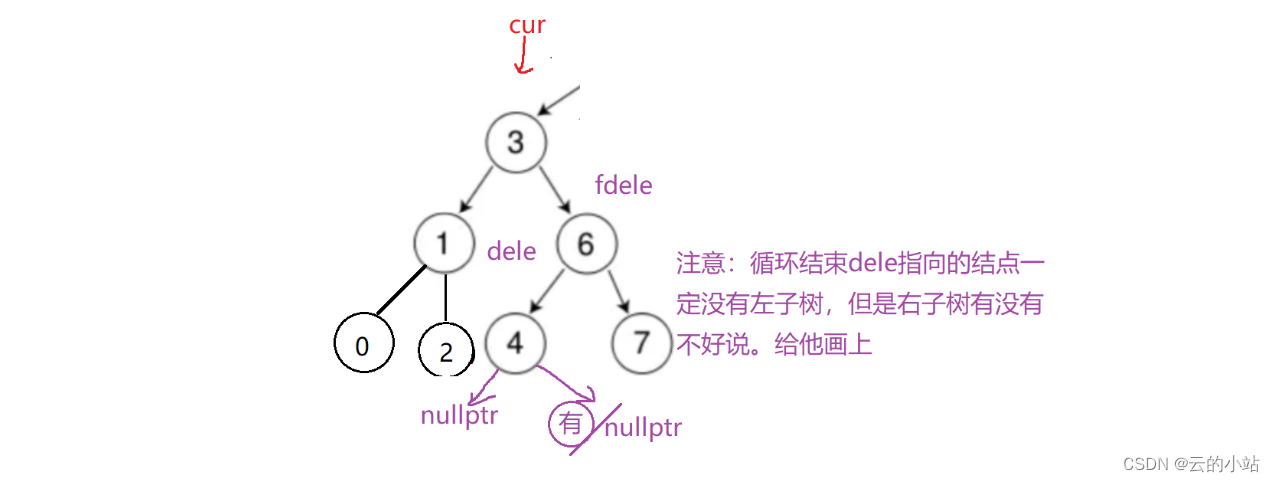
找到了，直接将dele->key赋值给cur->key
cur->key=dele->key;然后开始删除dele。
情况一，fdele!=cur；
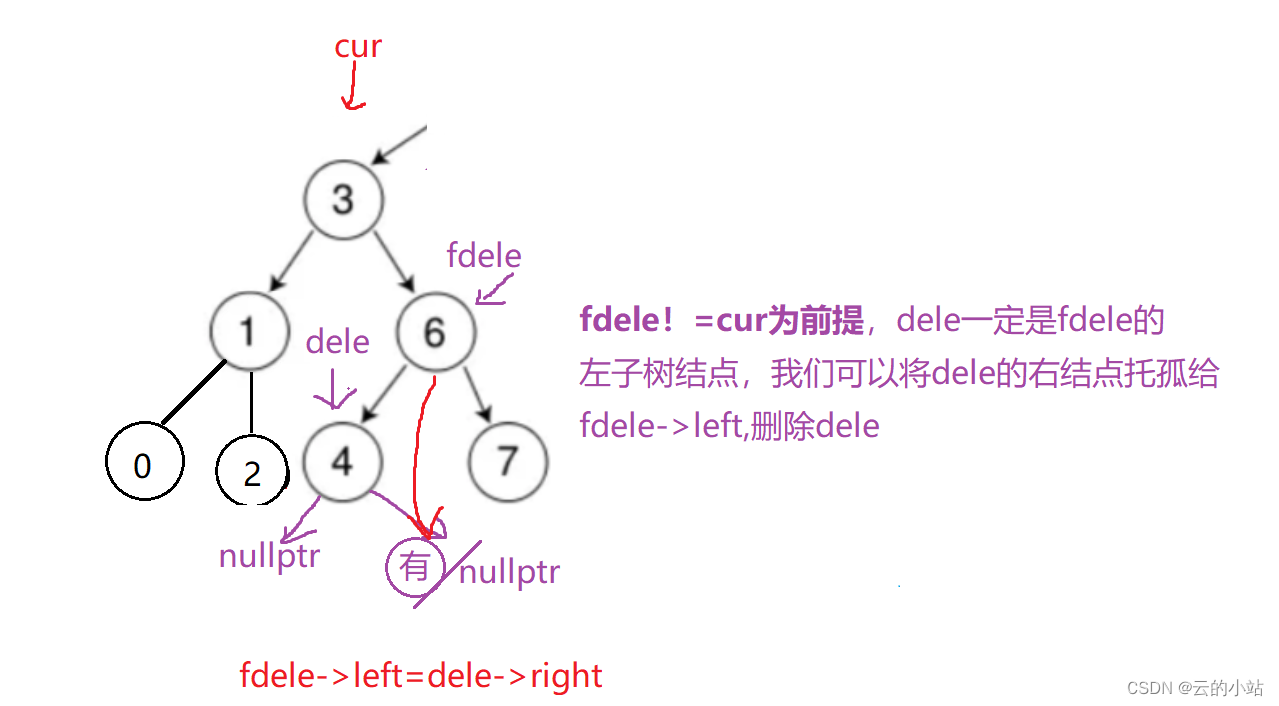
情况二：fdele==cur/dele=cur->left`；意味着并没有进入循环
链接后然后再删除dele
替换删除代码：
//判断左右子树是否为空，只要有一个为空就会进入第一种删除：普通删除结点
//+++++++++++++++++++++++++++++第一种开始++++++++++++++++++++++++++++++++
//cur的左树为空
if (cur->_left == nullptr)
{
//......
}
//cur的左树为空
else if (cur->_right == nullptr)
{
//......
}
//+++++++++++++++++++++++++++++第一种结束++++++++++++++++++++++++++++++++
//=============================替换删除==================================
else
{
//---替换法删除
Node* dele = cur->_right;
Node* fdele = cur;
while (dele->_left)
{
fdele = _cur;
dele = _cur->_left;
}
cur->_key = dele->_key;
//也解决了cur==root
if (fdele == cur)
//if(cur->right==dele)
{
fdele->_right = dele->_right;
}
else
{
fdele->_left = dele->_right;
}
delete dele;
}打印结点中序遍历
我们用中序遍历会发现出来的数据为排序好的。
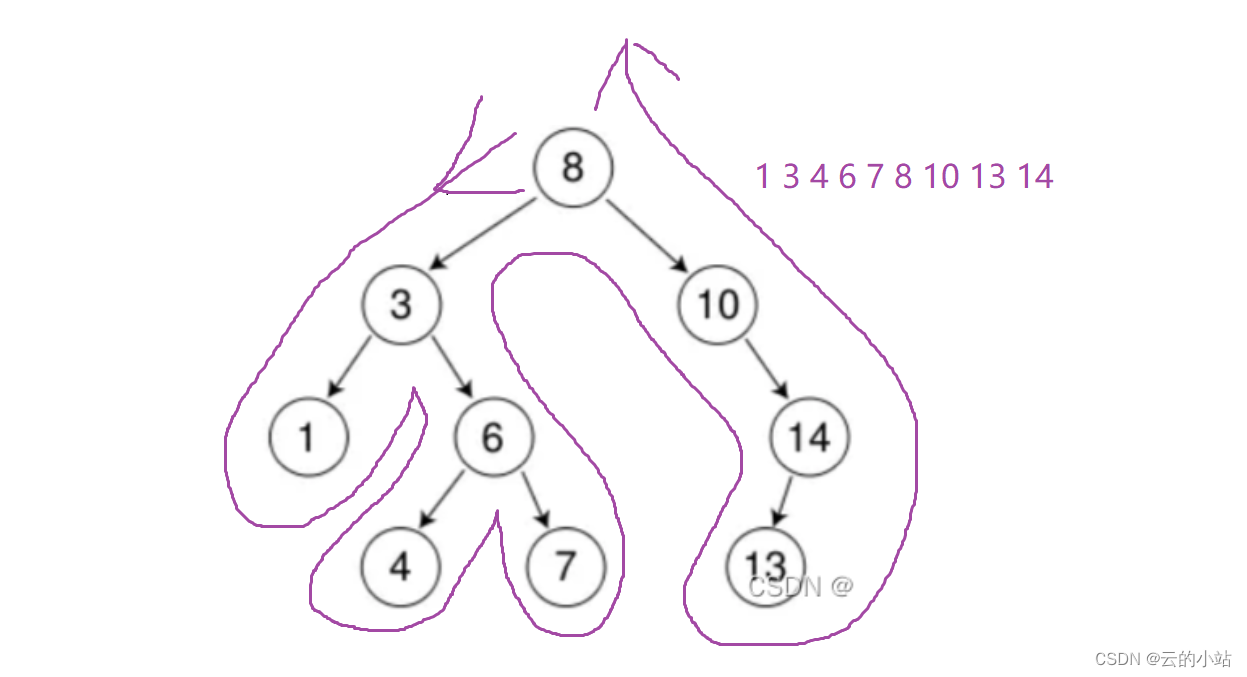
整体代码：（有R开头的就是递归写法，逻辑一样）
template<class K = int>
struct BSTreeNode
{
BSTreeNode(const K&key)
:_key(key)
{
_left = _right = nullptr;
}
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
};
template<class K=int>
class BSTree
{
typedef BSTreeNode<K> Node;
public：
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
}
else
{
Node* cur = _root;
Node* prev = cur;
while (cur != nullptr)
{
prev = cur;
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (prev->_key > cur->_key)
{
prev->_left = cur;
}
else
{
prev->_right = cur;
}
}
}
void Inorder()
{
_Inorder(_root);
}
bool RInsert(const K& key)
{
//if (!_root)
//{
// _root = new Node(key);
// return true;
//}
return _RInsert(_root, key);
}
Node* RFind(const K& key)
{
return _RFind(_root, key);
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur != nullptr)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
Node* Erase(const K& key)
{
Node* cur = _root;
Node* prev = cur;
while (cur != nullptr)
{
if (cur->_key < key)
{
prev = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
prev = cur;
cur = cur->_left;
}
else
{
//普通删除delete-->cur
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (prev->_left == cur)
{
prev->_left = cur->_right;
}
else
{
prev->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
}
//普通删除delete-->cur
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
else
{
if (prev->_left == cur)
{
prev->_left = cur->_left;
}
else
{
prev->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
}
else
{
//---替换法删除
Node* _cur = cur->_right;
Node* _prev = cur;
while (_cur->_left)
{
_prev = _cur;
_cur = _cur->_left;
}
cur->_key = _cur->_key;
//也解决了cur==root
if (_prev == cur)
{
_prev->_right = _cur->_right;
}
else
{
_prev->_left = _cur->_right;
}
//if (_prev->_left == _cur)
//{
// _prev->_left = cur->_right;
//}
//else
//{
// _prev->_right = cur->_right;
//}
delete _cur;
}
return cur;
}
}
return nullptr;
}
bool RErase(const K& key)
{
return _RErase(_root, key);
}
BSTree() = default;
BSTree<K>& operator=(BSTree<K> t)
{
std::swap(_root, t._root);
return *this;
}
~BSTree()
{
_Destroy(_root);
}
BSTree(BSTree<K>&t)
{
_root = _Copy(t._root);
}
private:
Node* _Copy(Node*&root)
{
if (root == nullptr)
{
return nullptr;
}
Node* copyRoot = new Node(root->_key);
copyRoot->_left = _Copy(root->_left);
copyRoot->_right = _Copy(root->_right);
return copyRoot;
}
void _Destroy(Node*&root)
{
if (root == nullptr)
{
return;
}
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
root = nullptr;
}
bool _RErase(Node*& root, const K&key)
{
if (root == nullptr)
{
return false;
}
if (key < root->_key)
{
return _RErase(root->_left, key);
}
else if(key>root->_key)
{
return _RErase(root->_right, key);
}
else
{
Node* del = root;
//普通删除
if (root->_left == nullptr)
{
root = root->_right;
}
//普通删除
else if(root->_right == nullptr)
{
root = root->_left;
}
//替换+递归删除
else
{
Node* _cur = root->_right;
Node* _prev = root;
while (_cur->_left)
{
_prev = _cur;
_cur = _cur->_left;
}
/*K tmp = _cur->_key;
RErase(tmp);
root->_key = tmp;*/
std::swap(root->_key, _cur->_key);
return _RErase(root->_right, key);
//if (_prev == root)
//{
// _prev->_right = _cur->_right;
//}
//else
//{
// _prev->_left = _cur->_right;
//}
}
delete del;
return true;
}
}
//bool _RInsert(Node* root, const K& key)
//{
// if (root->_left == nullptr && root->_key > key)
// {
// root->_left = new Node(key);
// return true;
// }
// if (root->_right == nullptr && root->_key < key)
// {
// root->_right = new Node(key);
// return true;
// }
// if (root->_key < key)
// {
// return _RInsert(root->_right, key);
// }
// else if (root->_key > key)
// {
// return _RInsert(root->_left, key);
// }
// else
// {
// return false;
// }
//}
bool _RInsert(Node*& root, const K& key)
{
//神之一笔：引用上级子树的引用，这里先当与
//（上一级）root->left(right)=new Node(key)
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (key > root->_key)
{
return _RInsert(root->_right, key);
}
else if(key<root->_key)
{
return _RInsert(root->_left, key);
}
else
{
return false;
}
}
Node* _RFind(Node*root,const K& key)
{
if (root == nullptr)
{
return nullptr;
}
if (root->_key < key)
{
return _RFind(root->_right,key);
}
else if (root->_key > key)
{
return _RFind(root->_left, key);
}
else
{
return root;
}
}
void _Inorder(Node* root)
{
if (root == nullptr)
{
return;
}
_Inorder(root->_left);
std::cout << root->_key << ' ';
_Inorder(root->_right);
}
Node* _root = nullptr;
};
