一、定义

• 卡方检验属于非参数检验，由于非参检验不存在具体参数和总体正态分布的假设，所以有时被称为自由分布检验。
• 原假设$H_0$：观察频数与期望频数没有显著性差异

二、用途

1. 检验某个连续变量的分布是否与某种理论分布相一致。例如是否符合正态分布，均匀分布，Poisson(泊松)分布
2. 检验某个分类变量的各类的概率是否等于指定概率
3. 检验某两个分类变量是否 相互独立
4. 检测两种方法的检测结果是否一致
5. 检测控制某种或某几种的变量后，另外两个分类变量是否相互独立。

三、公式

$${\chi }^2=\sum \frac{(A-E{)}^2}{E}=\sum _{i=1}^k\frac{(A_i-n{p}_i{)}^2}{n{p}_i}$$

其中：$A_i$为单元格 $i$ 中的观察值，$p_i$为单元格 $i$ 中的在$H_0$假设前提下的概率，$k$ 为单元格数.

四、案例

• 案例来源：统计学——卡方检验和卡方分布

	感冒人数	未感冒人数	合计	感冒率
喝牛奶组	43	96	139	30.94%
不喝牛奶组	28	84	112	25.00%
合计	71	180	251	28.29%

4.1 手工统计

1. 提出假设：喝牛奶对感冒发病率是没有影响
2. 从表得知整体感冒率为28.29%，那么根据原假设（喝牛奶和患上感冒是独立无关的），反推出理论上的感冒人数：

	感冒人数	未感冒人数	合计
喝牛奶组	=139*0.2829	=139*(1-0.2829)	139
不喝牛奶组	=112*0.2829	=112*(1-0.2829)	112

如果喝牛奶和感冒真的是独立无关的，那么理论值和实际值差别应该会很小。

3. 根据卡方检验的公式，计算得：

$$\begin{array}{rl}& {\chi }^2=\frac{(43-139\ast 0.2829{)}^2}{139\ast 0.2829}+\frac{(28-112\ast 0.2829{)}^2}{112\ast 0.2829}+\frac{[96-139\ast (1-0.2829){]}^2}{139\ast (1-0.2829)}+\frac{[84-112\ast (1-0.2829){]}^2}{112\ast (1-0.2829)}\\ & \\ & =1.077\end{array}$$

4. 查询卡方分布临界值：统计分布临界值表

上述例子中，自由度$k=(2-1)\ast (2-1)=1$；【自由度 = （行数-1）*（列数-1）】

我们看到，${\chi }^2$分布在自由度$k=1，p=0.05$时的取值为3.84。

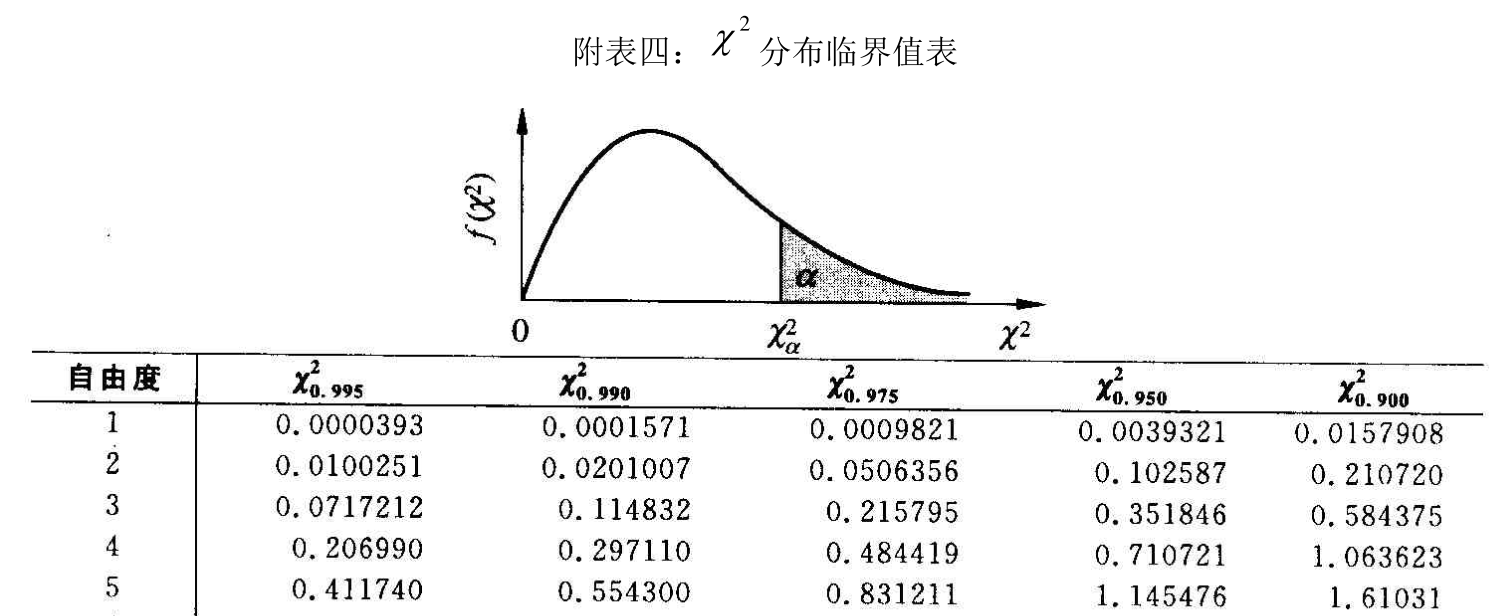
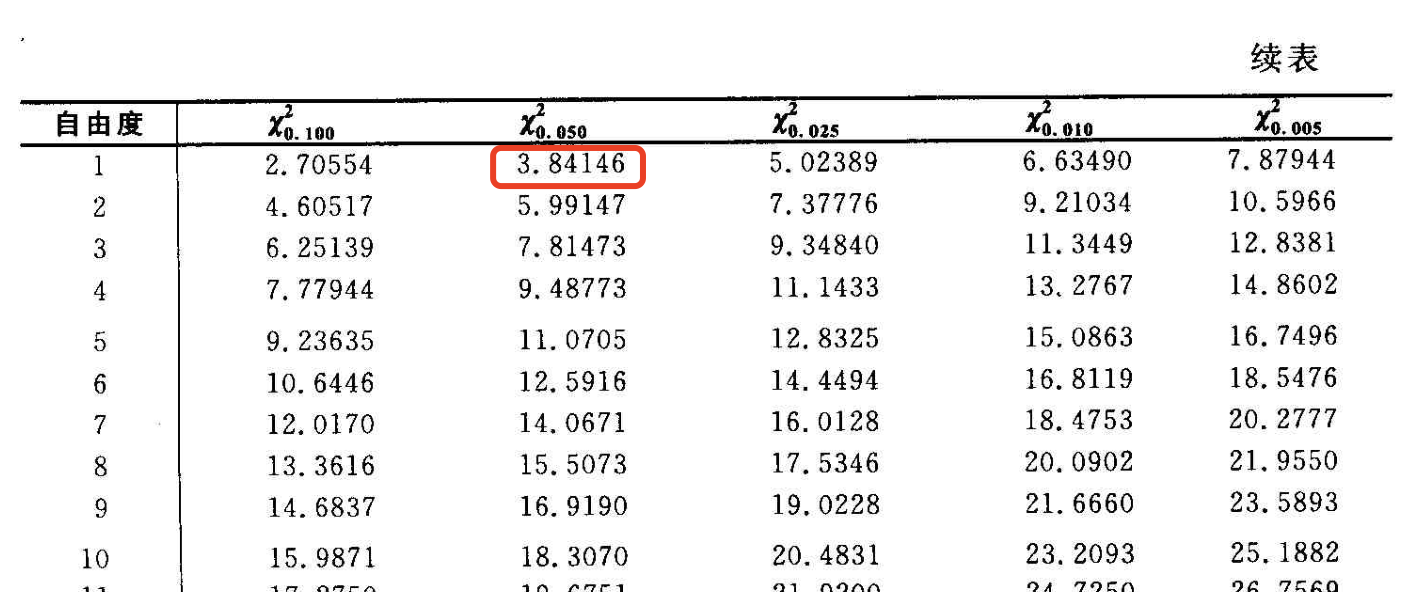
5. 我们计算得到的${\chi }^2$值1.077，小于3.84，故不能拒绝原假设H0 ，即喝牛奶对感冒发病率没有影响（即喝牛奶与感冒无关）

4.2 python统计

from scipy.stats import chi2_contingency

# 构建一个 2x2 的列联表数据
obs = [[43, 96], [28, 84]]

# 执行卡方检验，
# correction 如果设置为 True，则应用 Yates 的连续性校正（Yates' continuity correction），以弥补数据过于稀疏时可能导致的偏差；如果设置为 False，则不使用该校正。
chi2, p_value, dof, expected_freq = chi2_contingency(obs,correction=False)

# 输出结果
print("卡方值：", chi2)
print("P 值：", p_value)
print("自由度：", dof)
print("期望频率：", expected_freq)

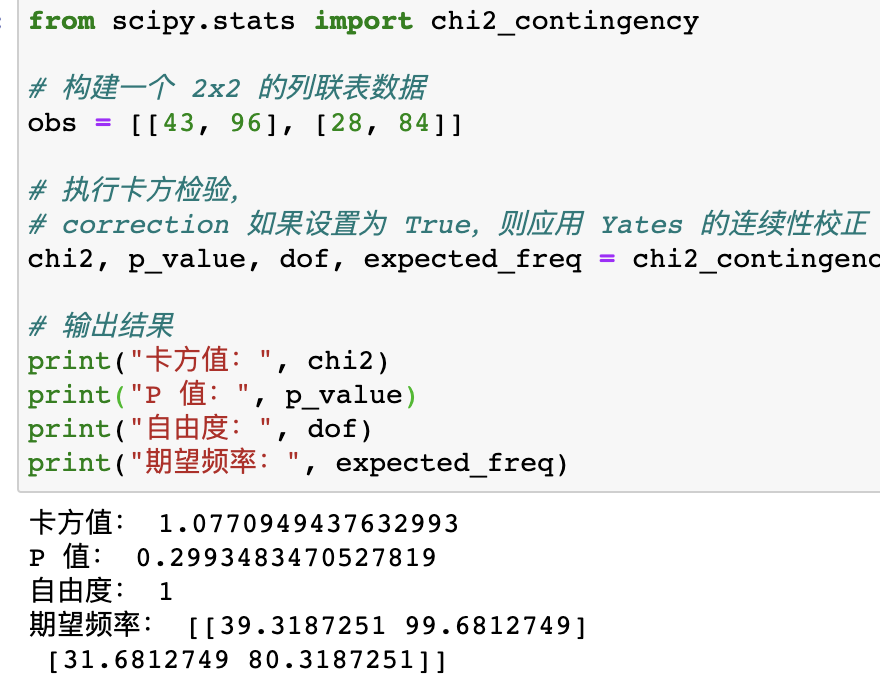
• 可以看出结果与上文一致

4.3 SPSS统计

参考：数据分析之卡方检验

• 步骤1：导入数据

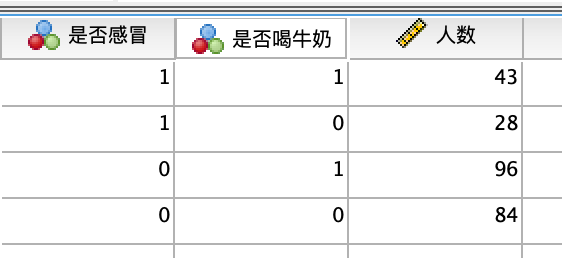
• 步骤2：数据加权处理

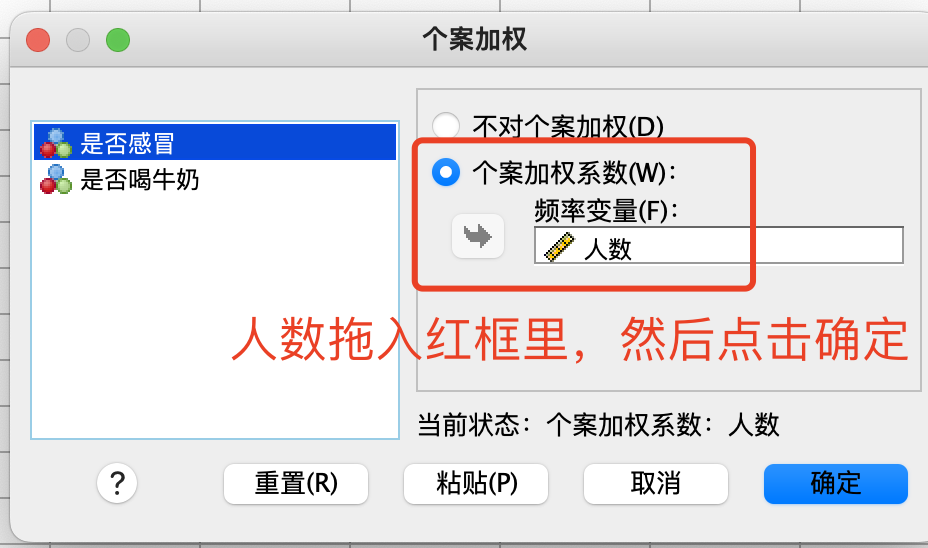
• 步骤3：交叉表分析

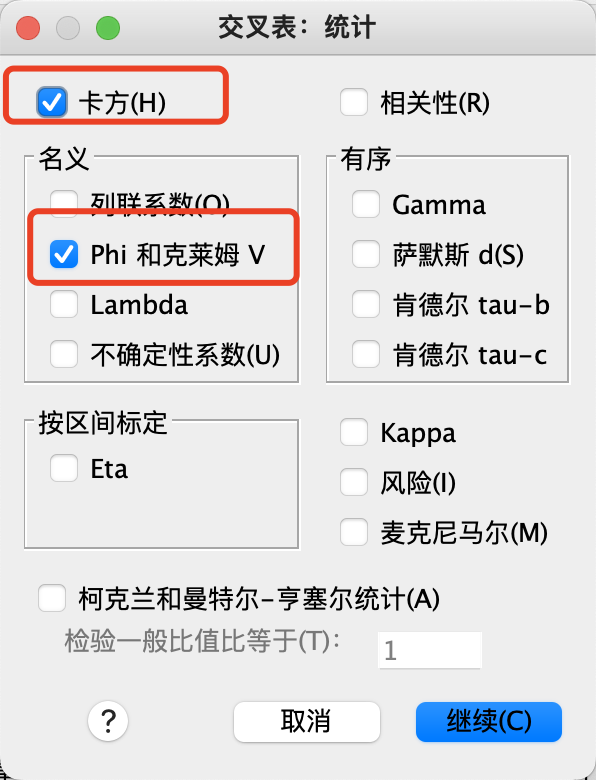
选项都勾选好之后，点击确定，即得到以下结果：

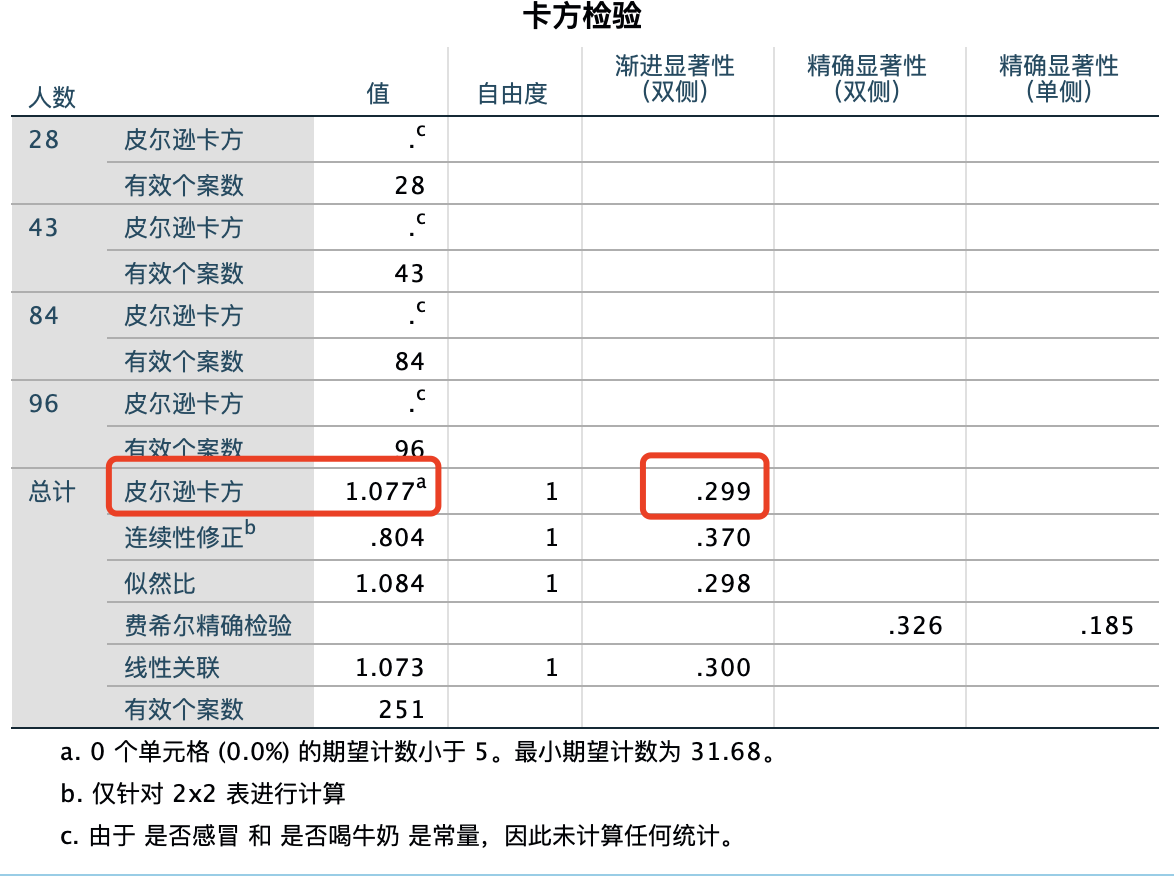
可以得到卡方值为1.077，p值为0.299，与上文一致。