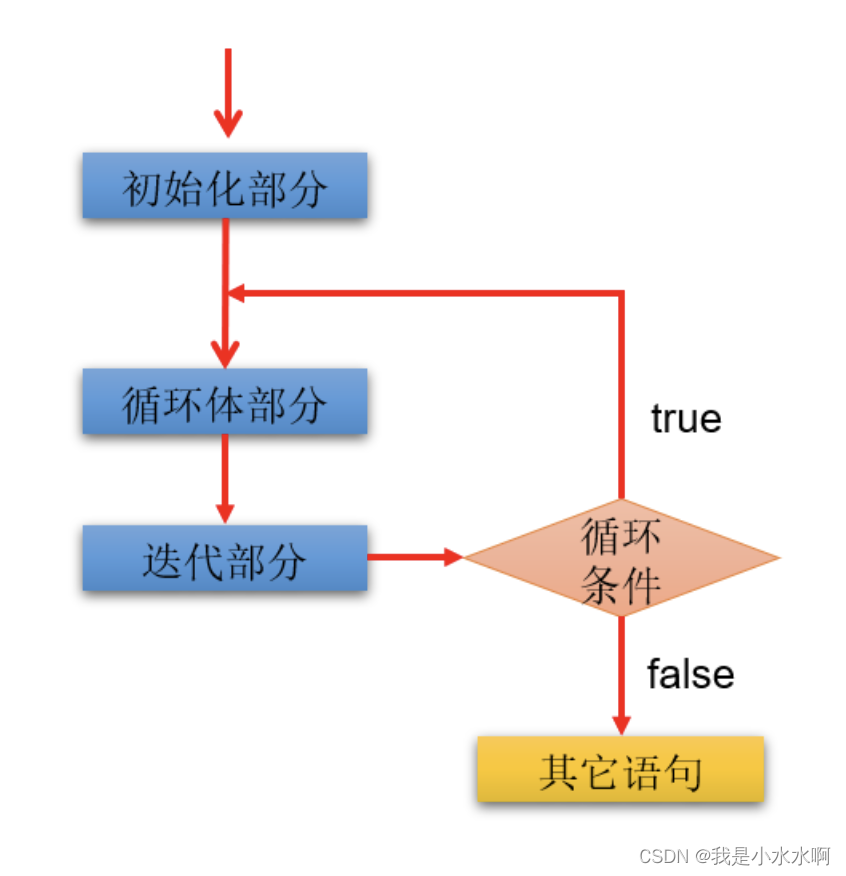
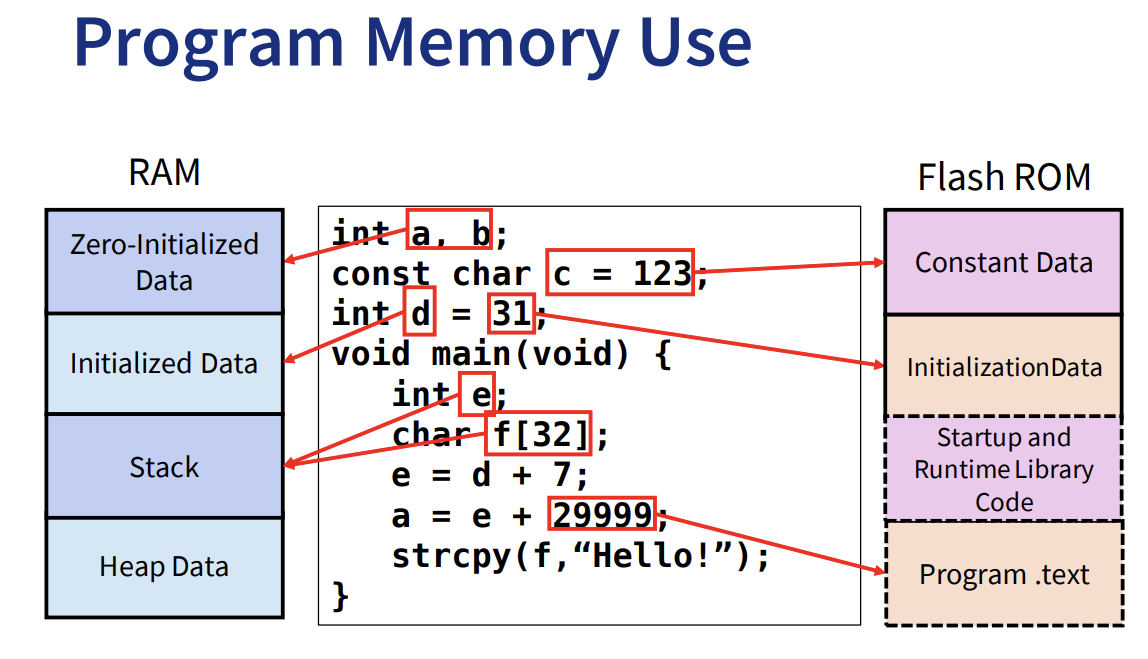
图像雅可比矩阵原理与推导
理想情况下，图像像素坐标系和图像物理坐标系无倾斜，则二者坐标转换关系如下，且两边求导：
[
u
v
1
]
=
[
1
d
x
0
u
0
0
1
d
y
v
0
0
0
1
]
[
x
y
1
]
(1)
\begin{bmatrix}u\\v\\1\end{bmatrix}=\begin{bmatrix}\frac{1}{d_x}&0&u_0\\0&\frac{1}{d_y}&v_0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} \tag{1}
uv1
=
dx1000dy10u0v01
xy1
(1)
{
u
˙
=
1
d
x
x
˙
v
˙
=
1
d
y
y
˙
(2)
\begin{cases}\dot{u}=\frac{1}{d_x}\dot{x}\\ \dot{v}=\frac{1}{d_y}\dot{y}\end{cases} \tag{2}
{u˙=dx1x˙v˙=dy1y˙(2)由小孔成像原理，空间一点的相机坐标和图像物理坐标转换关系如下，且两边求导：
[
x
y
1
]
=
[
f
Z
c
0
0
0
f
Z
c
0
0
0
1
Z
c
]
[
X
c
Y
c
Z
c
]
(3)
\begin{bmatrix}x\\ y\\ 1\end{bmatrix}=\begin{bmatrix}\frac{f}{Z_c}&0&0\\ 0&\frac{f}{Z_c}&0\\ 0&0&\frac{1}{Z_c}\end{bmatrix}\begin{bmatrix}X_c\\ Y_c\\ Z_c\end{bmatrix} \tag{3}
xy1
=
Zcf000Zcf000Zc1
XcYcZc
(3)
{
x
˙
=
f
(
X
˙
c
Z
c
−
X
c
Z
˙
c
Z
c
2
)
=
f
X
˙
c
Z
c
−
x
Z
˙
c
Z
c
y
˙
=
f
(
Y
˙
c
Z
c
−
Y
c
Z
˙
c
Z
c
2
)
=
f
Y
˙
c
Z
c
−
y
Z
˙
c
Z
c
(4)
\begin{cases}\dot{x}=f(\frac{\dot{X}_c}{Z_c}-\frac{X_c\dot{Z}_c}{Z_c^2})=\frac{f\dot{X}_c}{Z_c}-\frac{x\dot{Z}_c}{Z_c}\\ \dot{y}=f(\frac{\dot{Y}_c}{Z_c}-\frac{Y_c\dot{Z}_c}{Z_c^2})=\frac{f\dot{Y}_c}{Z_c}-\frac{y\dot{Z}_c}{Z_c}\end{cases} \tag{4}
{x˙=f(ZcX˙c−Zc2XcZ˙c)=ZcfX˙c−ZcxZ˙cy˙=f(ZcY˙c−Zc2YcZ˙c)=ZcfY˙c−ZcyZ˙c(4)固定相机，移动空间点时，速度关系为：
p
˙
c
=
c
v
p
+
c
ω
p
×
p
c
(5)
\dot{\boldsymbol{p}}_c =^c\boldsymbol{v}_p +^c\boldsymbol{\omega}_p\times\boldsymbol{p}_c\tag{5}
p˙c=cvp+cωp×pc(5)固定空间点，移动相机时，速度关系为：
p
˙
c
=
−
c
v
c
−
c
ω
c
×
p
c
(6)
\dot{\boldsymbol{p}}_c = -^c\boldsymbol{v}_c -^c\boldsymbol{\omega}_c\times\boldsymbol{p}_c\tag{6}
p˙c=−cvc−cωc×pc(6)
{
X
˙
c
=
−
c
ν
c
,
x
−
c
ω
c
,
y
Z
c
+
c
ω
c
,
z
Y
c
Y
˙
c
=
−
c
ν
c
,
y
−
c
ω
c
,
z
X
c
+
c
ω
c
,
x
Z
c
Z
˙
c
=
−
c
ν
c
,
z
−
c
ω
c
,
x
Y
c
+
c
ω
c
,
y
X
c
(7)
\begin{cases}\dot{X}_c=-{}^c\nu_{c,x}-{}^c\omega_{c,y}Z_c+{}^c\omega_{c,z}Y_c\\ \dot{Y}_c=-{}^c\nu_{c,y}-{}^c\omega_{c,z}X_c+{}^c\omega_{c,x}Z_c\\ \dot{Z}_c=-{}^c\nu_{c,z}-{}^c\omega_{c,x}Y_c+{}^c\omega_{c,y}X_c\end{cases}\tag{7}
⎩
⎨
⎧X˙c=−cνc,x−cωc,yZc+cωc,zYcY˙c=−cνc,y−cωc,zXc+cωc,xZcZ˙c=−cνc,z−cωc,xYc+cωc,yXc(7)将(7)代入(4)，得：
{
x
˙
=
−
f
Z
c
c
v
c
,
x
+
x
Z
c
c
v
c
,
z
+
x
y
f
c
ω
c
,
x
−
f
2
+
x
2
f
c
ω
c
,
y
+
y
c
ω
c
,
z
y
˙
=
−
f
Z
c
c
v
c
,
y
+
y
Z
c
c
v
c
,
z
+
f
2
+
y
2
f
c
ω
c
,
x
−
x
y
f
c
ω
c
,
y
−
x
c
ω
c
,
z
(8)
\left\{\begin{array}{l} \dot{x}=-\frac{f}{Z_{c}}{ }^{c} v_{c, x}+\frac{x}{Z_{c}}{ }^{c} v_{c, z}+\frac{x y}{f}{ }^{c} \omega_{c, x}-\frac{f^{2}+x^{2}}{f}{ }^{c} \omega_{c, y}+y^{c} \omega_{c, z} \\ \dot{y}=-\frac{f}{Z_{c}}{ }^{c} v_{c, y}+\frac{y}{Z_{c}}{ }^{c} v_{c, z}+\frac{f^{2}+y^{2}}{f}{ }^{c} \omega_{c, x}-\frac{x y}{f}{ }^{c} \omega_{c, y}-x^{c} \omega_{c, z} \end{array}\right.\tag{8}
{x˙=−Zcfcvc,x+Zcxcvc,z+fxycωc,x−ff2+x2cωc,y+ycωc,zy˙=−Zcfcvc,y+Zcycvc,z+ff2+y2cωc,x−fxycωc,y−xcωc,z(8)即：
[
x
˙
y
˙
]
=
[
−
f
Z
c
0
x
Z
c
x
y
f
−
f
2
+
x
2
f
y
0
−
f
Z
c
y
Z
c
f
2
+
y
2
f
−
x
y
f
−
x
]
[
c
v
c
,
x
c
v
c
,
y
c
v
c
,
z
c
ω
c
,
x
c
ω
c
,
y
c
ω
c
,
z
]
(9)
\begin{bmatrix}\dot{x}\\ \dot{y}\end{bmatrix}=\begin{bmatrix}-\frac{f}{Z_c}&0&\frac{x}{Z_c}&\frac{xy}{f}&-\frac{f^2+x^2}{f}&y\\ 0&-\frac{f}{Z_c}&\frac{y}{Z_c}&\frac{f^2+y^2}{f}&-\frac{xy}{f}&-x\end{bmatrix}\left[\begin{array}{l} { }^{c} v_{c, x} \\ { }^{c} v_{c, y} \\ { }^{c} v_{c, z} \\ { }^{c} \omega_{c, x} \\ { }^{c} \omega_{c, y} \\ { }^{c} \omega_{c, z} \end{array}\right]\tag{9}
[x˙y˙]=[−Zcf00−ZcfZcxZcyfxyff2+y2−ff2+x2−fxyy−x]
cvc,xcvc,ycvc,zcωc,xcωc,ycωc,z
(9)将(9)以及
x
=
d
x
(
u
−
u
0
)
x=d_{x}\left(u-u_{0}\right)
x=dx(u−u0)和
y
=
d
y
(
v
−
v
0
)
y=d_y(v-v_0)
y=dy(v−v0)代入(2)：
[
u
˙
v
˙
]
=
[
−
f
d
x
Z
c
0
(
u
−
u
0
)
Z
c
(
u
−
u
0
)
d
y
(
v
−
v
0
)
f
−
f
2
+
d
x
2
(
u
−
u
0
)
2
d
x
f
d
y
(
v
−
v
0
)
d
x
0
−
f
d
y
Z
c
(
v
−
v
0
)
Z
c
f
2
+
d
y
2
(
v
−
v
0
)
2
d
y
f
−
d
x
(
u
−
u
0
)
(
v
−
v
0
)
f
−
d
x
(
u
−
u
0
)
d
y
]
[
c
v
c
,
x
c
v
c
,
y
c
v
c
,
z
c
ω
c
,
x
c
ω
c
,
y
c
ω
c
,
z
]
(10)
\left[\begin{array}{c} \dot{u} \\ \dot{v} \end{array}\right]=\left[\begin{array}{cccccc} -\frac{f}{d_{x} Z_{c}} & 0 & \frac{\left(u-u_{0}\right)}{Z_{c}} & \frac{\left(u-u_{0}\right) d_{y}\left(v-v_{0}\right)}{f} & -\frac{f^{2}+d_{x}^{2}\left(u-u_{0}\right)^{2}}{d_{x} f} & \frac{d_{y}\left(v-v_{0}\right)}{d_{x}} \\ 0 & -\frac{f}{d_{y} Z_{c}} & \frac{\left(v-v_{0}\right)}{Z_{c}} & \frac{f^{2}+d_{y}^{2}\left(v-v_{0}\right)^{2}}{d_{y} f} & -\frac{d_{x}\left(u-u_{0}\right)\left(v-v_{0}\right)}{f} & -\frac{d_{x}\left(u-u_{0}\right)}{d_{y}} \end{array}\right]\left[\begin{array}{l} { }^{c} v_{c, x} \\ { }^{c} v_{c, y} \\ { }^{c} v_{c, z} \\ { }^{c} \omega_{c, x} \\ { }^{c} \omega_{c, y} \\ { }^{c} \omega_{c, z} \end{array}\right] \tag{10}
[u˙v˙]=
−dxZcf00−dyZcfZc(u−u0)Zc(v−v0)f(u−u0)dy(v−v0)dyff2+dy2(v−v0)2−dxff2+dx2(u−u0)2−fdx(u−u0)(v−v0)dxdy(v−v0)−dydx(u−u0)
cvc,xcvc,ycvc,zcωc,xcωc,ycωc,z
(10)即：
[
u
˙
v
˙
]
=
J
i
m
g
[
c
v
c
c
u
c
]
(11)
\begin{bmatrix}\dot{u}\\ \dot{v}\end{bmatrix}=J_{img}\begin{bmatrix}^c\boldsymbol{v}_{c}\\^c \boldsymbol{u}_{c}\end{bmatrix}\tag{11}
[u˙v˙]=Jimg[cvccuc](11)可得图像雅可比矩阵：
J
i
m
g
=
[
−
f
d
x
Z
c
0
(
u
−
u
0
)
Z
c
(
u
−
u
0
)
d
y
(
v
−
v
0
)
f
−
f
2
+
d
x
2
(
u
−
u
0
)
2
d
x
f
d
y
(
v
−
v
0
)
d
x
0
−
f
d
y
Z
c
(
v
−
v
0
)
Z
c
f
2
+
d
y
2
(
v
−
v
0
)
2
d
y
f
−
d
x
(
u
−
u
0
)
(
v
−
v
0
)
f
−
d
x
(
u
−
u
0
)
d
y
]
(12)
J_{img}=\left[\begin{array}{cccccc} -\frac{f}{d_{x} Z_{c}} & 0 & \frac{\left(u-u_{0}\right)}{Z_{c}} & \frac{\left(u-u_{0}\right) d_{y}\left(v-v_{0}\right)}{f} & -\frac{f^{2}+d_{x}^{2}\left(u-u_{0}\right)^{2}}{d_{x} f} & \frac{d_{y}\left(v-v_{0}\right)}{d_{x}} \\ 0 & -\frac{f}{d_{y} Z_{c}} & \frac{\left(v-v_{0}\right)}{Z_{c}} & \frac{f^{2}+d_{y}^{2}\left(v-v_{0}\right)^{2}}{d_{y} f} & -\frac{d_{x}\left(u-u_{0}\right)\left(v-v_{0}\right)}{f} & -\frac{d_{x}\left(u-u_{0}\right)}{d_{y}} \end{array}\right]\tag{12}
Jimg=
−dxZcf00−dyZcfZc(u−u0)Zc(v−v0)f(u−u0)dy(v−v0)dyff2+dy2(v−v0)2−dxff2+dx2(u−u0)2−fdx(u−u0)(v−v0)dxdy(v−v0)−dydx(u−u0)
(12)如有不足之处欢迎指出~
