1 描述

给一字符串 s, 找出在 s 中的最长回文子序列的长度. 你可以假设 s 的最大长度为 1000.

2 样例

2.1 样例1

输入： “bbbab”
输出： 4
解释：
一个可能的最长回文序列为 “bbbb”

2.2 样例2

输入： “bbbbb”
输出： 5

3 解题思路以及实现方法

3.1 解题思路

3.1.1 确定状态

最优策略产生最长的回文子串T，其长度为M；

情况1：回文串长度为1，既只包含一个字母
情况2：回文串长度大于1，则T[0] == T[M - 1]
对于情况2，剩余部分T[1…M - 2]仍然是一个回文串

子问题：
要求s[i…j]的最长回文子串
如果s[i] == s[j]，需要知道s[i + 1, j + 1]的最长回文子串，否则，答案是s[i + 1 … j]的最长回文子串或s[i, …, j - 1]的最长回文子串
状态：设f[i][j]表示为s[i … j]的最长回文子串的长度

3.1.2 转移方程

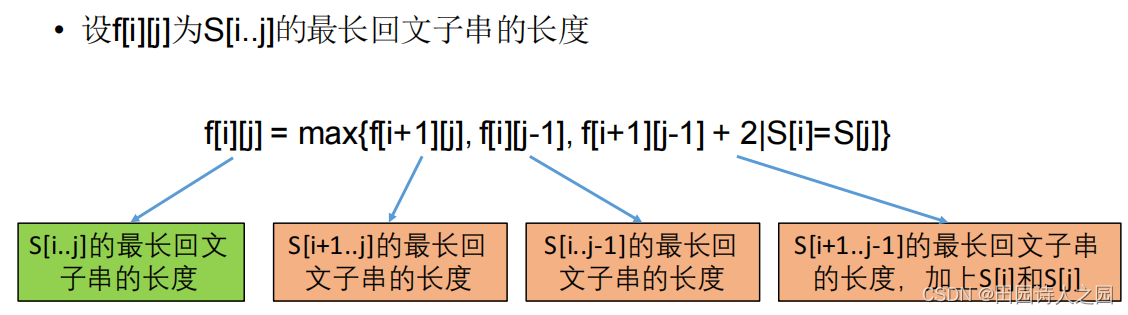
在这里插入图片描述

3.1.3 初始条件和边界情况

状态：设f[i][j]表示为s[i … j]的最长回文子串的长度
f[i][j] = max{f[i+1][j], f[i][j-1], f[i+1][j-1] + 2|S[i]=S[j]}

初始条件：

f[0][0] = f[1][1] = … = f[N-1][N-1] = 1
- 一个字母，既长度为1的回文串
如果s[i] == s[i + 1]，f[i][i + 1] = 2
如果s[i] != s[i + 1]，f[i][i + 1] = 1

3.1.4 计算顺序

设f[i][j]表示为s[i … j]的最长回文子串的长度
f[i][j] = max{f[i+1][j], f[i][j-1], f[i+1][j-1] + 2|S[i]=S[j]}
区间动态规划：按照长度j - i 从小到大一次去计算。

3.2 题解

3.2.1 C++实现

class Solution {
public:
    /**
     * @param s: the maximum length of s is 1000
     * @return: the longest palindromic subsequence's length
     */
    int longestPalindromeSubseq(string &s) {
        // write your code here
        int n = s.size();

        if (n <= 1) {
            return n;
        }

        vector<vector<int>> f(n, vector<int>(n, 1));

        for (int i = 0; i < n - 1; i++) {
            f[i][i + 1] = (s[i] == s[i + 1]) ? 2 : 1;
        }

        for (int len = 3; len <= n; len++) {
            for (int i = 0; i <= n - len; i++) {
                int j = i + len - 1;
                f[i][j] = max(f[i + 1][j], f[i][j - 1]);
                if (s[i] == s[j]) {
                    f[i][j] = max(f[i][j], f[i + 1][j - 1] + 2);
                }
            }
        }

        return f[0][n - 1];
    }
};

3.2.2 java实现

public class Solution {
    /**
     * @param s: the maximum length of s is 1000
     * @return: the longest palindromic subsequence's length
     */
    public int longestPalindromeSubseq(String s) {
        // write your code here
        char[] str = s.toCharArray();
        int n = str.length;
        if (n <= 1) {
            return n;
        }

        int[][] f = new int[n][n];

        for (int i = 0; i < n; i++) {
            f[i][i] = 1;
        }

        for (int i = 0; i < n - 1; i++) {
            f[i][i + 1] = (str[i] == str[i + 1]) ? 2 : 1;
        }

        for (int len = 3; len <= n; len++) {
            for (int i = 0; i <= n - len; i++) {
                int j = i + len - 1;
                f[i][j] = Math.max(f[i + 1][j], f[i][j - 1]);
                if (str[i] == str[j]) {
                    f[i][j] = Math.max(f[i][j], f[i + 1][j - 1] + 2);
                }
            }
        }

        return f[0][n - 1];
    }
}