数据链路层的研究思想

本章研究数据链路层的基本思想是当A要给B发送数据，那么就是从A的数据链路层，自左向右发送的，如图箭头所示

数据链路层基本概念

结点：指主机和路由器，用同一条线连在一起的主机或路由器叫做相邻结点
链路：网络中两个结点之间的物理通道，链路的传输介质主要有双绞线、光纤和微波。分为有线链路、无线链路
数据链路：网络中两个结点之间的逻辑链路，把实现控制数据传输协议的硬件和软件加到链路上就构成数据链路
帧：链路层的协议数据单元，封装网络层数据报

数据链路层负责通过一条链路从一个结点向另一个物理链路直接相连的相邻结点传送数据报

数据链路层功能概述

数据链路层在物理层提供服务的基础上向网络层提供服务， 其最基本的服务是将源自网络层来的数据可靠地传输到相邻节点的目标机网络层。 其主要作用是加强物理层传输原始比特流的功能， 将物理层提供的可能出错的物理连接改造成为逻辑上无差错的数据链路， 使之对网络层表现为一 一条无差错的链路。

物理层容易把数据弄丢，数据链路层就需要把可能要发生的差错预知好，然后进行一定的差错控制，给网络层提供一个无差错的服务

为网络层提供服务

• 无确认的无连接服务。源机器发送数据顿时不需先建立链路连接，目的机器收到数据顿时不需发回确认。对丢失的帧，数据链路层不负责重发而交给上层处理。适用于实时通信或误码率较低的通信信道，如以太网。

• 有确认的无连接服务。源机器发送数据顿时不需先建立链路连接，但目的机器收到数据帧时必须发回确认。源机器在所规定的时间内未收到确定信号时，就重传丢失的帧，以提高传输的可靠性。该服务适用于误码率较高的通信信道，如无线通信。

• 有确认的面向连接服务。帧传输过程分为三个阶段：建立数据链路、传输帧、释放数据链路。目的机器对收到的每一帧都要给出确认，源机器收到确认后才能发送下一帧，因而该服务的可靠性最高。该服务适用于通信要求（可靠性、实时性）较高的场合。

  有链接就一定要确认，即不存在无确认的面向连接的服务

链路管理

数据链路层连接的建立、维持和释放的过程称为链路管理，它主要用于面向连接的服务

帧定界、帧同步与透明传输（组帧）

封装成帧

封装成帧就是在一段数据的前后部分添加首部和尾部，这样就构成了一个帧。接收端在收到物理层上交的比特流后，就能根据首部和尾部的标记，从收到的比特流中识别帧的开始和结束

首部和尾部包含许多的控制信息，他们的一个重要作用：帧定界（确定帧的界限）

帧同步：接收方应当能从接收到的二进制比特流中区分出帧的起始和终止

为了提高帧的传输速率，应当使帧的数据部分长度尽可能地大于首部和尾部的长度，但每种数据链路层协议都规定了帧的数据部分和长度上限，即最大传输单元

透明传输

透明传输是指不管所传数据是什么样的比特组合，都应当能够在链路上传送。因此，链路层就“看不见”有什么妨碍数据传输的东西
当所传数据中的比特组合恰巧与某一个控制信息完全一样时，就必须采取适当的措施，使接收方不会将这样的数据误认为是某种控制信息。这样才能保证数据链路层的传输是透明的

例如上面boss和秘书的例子，boss让秘书传五分文件给B公司，秘书不知道文件里面有什么，只管传输就可以了

组帧方法

字符计数法

帧首部使用一个计数字段（第一个字节，八位）来表明帧内字符数

问题：如果某一个计数字段错误，后面全都错误

字符填充法

SOH（start of header）：首部的第一个字节
EOT（end of transmission）：尾部的最后一个字节

• 当传送的帧是由文本文件组成时（文本文件的字符都是从键盘上输入的，都是ASCLL码），任意本文都与上述两个字节都不同，因此不管从键盘上输入什么字符都可以放在帧里传过去，即透明传输
• 当传送的帧是由非ASCLL码的文本文件组成时（而今知道吗的程序或图像等），就有可能与上述两个字节相同，因此就要采用字符填充方法实现透明传输

ESC：转义字符，不用管后面的字符

字符填充法也就是在发送端的时候添加转义字符，在接收端的时候把所有转义字符去掉，剩下的就是原始数据

零比特填充法

注意开始和结束标志字节是0+6个1+0

操作：

• 在发送端，扫描整个信息字段，只要连续5个1就立即填入一个0
  这样就保证在数据部分不会有和标志字节相同的字节
• 在接收端收到一个帧是，先找到标志字段确定边界，再用硬件对比特流进行扫描，发送连续5个1时，就把后面的0删除

保证了透明传输：在传输的比特流中可以传送任意比特组合，而不会引起对帧边界的判断错误

违规编码法

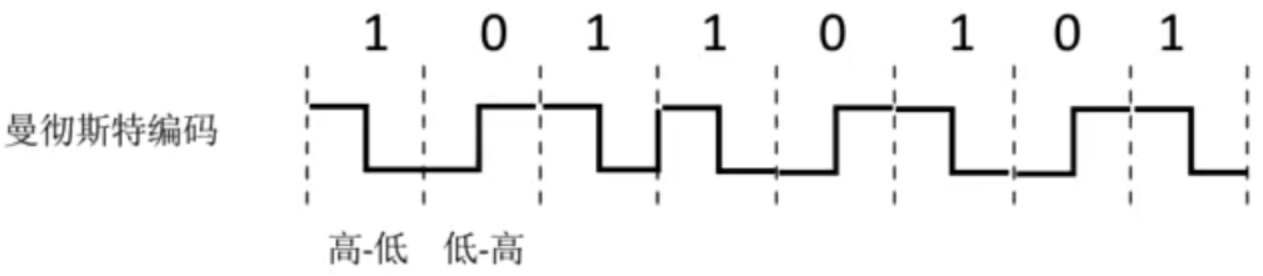
可以用“高-高”、“低-低”（也就是编码中不同的电平）来定界帧的起始和终止

由于字节计数法汇总Count字段（起始字节）的脆弱性（其值若有差错将导致灾难性后果）及字符填充法实现上的复杂性和不兼容性，目前较为普遍使用的帧同步法是比特填充法和违规编码法

流量控制

关于可靠传输、滑动窗口、流量控制

可靠传输：发送端发什么，接收端收到什么，中间不会出现失序，出错等问题
流量控制：控制发送速率，使接受方有足够的缓冲空间来接收每一个帧
滑动窗口解决

• 流量控制，也就是收不下就不给确认，想发也发不了
• 可靠传输，通过发送方自动重传

较高的发送速度和较低的接受能力的不匹配，会造成传输出错，因此流量控制也是数据链路层的一项重要工作

数据链路层的流量控制是点到点的，传输层的流量控制是端到端的
数据链路层流量控制手段是接收方收不下就不回复确认帧，传输层流量控制手段是接收端给发送端一个窗口公告，告诉发送端接收端当前窗口有多少、缓冲区还有多大等
例如，一个主人给猫喂食，把食物和装食物的盘子放到屋子里，如果猫吃完了，没吃饱，就会叼着盘子，送给主人，主人再加食物，如果没把盘子送回来，就认为猫吃饱了，不在加食物

停止-等待协议

每发送完一个帧就停止发送，等待对方的确认，在收到确认后再发送下一个帧

研究停止等待协议的前提

• 虽然现在常用全双工通信方式，但是为了讨论问题方便，仅考虑一方发送数据（发送方）一方接收数据（接收方）
• 因为是在讨论可靠传输的原理，所以并不考虑数据是在哪一个层次上传送的
• 停止等待就是每发送完一个分组就停止发送，等待对方确认，在收到确认后再发送下一个分组

停等协议-无差错情况

这里0被重复利用了，只是编号相同，但是帧本身并不同，因为每发送一个数据帧就停止并等待，因此用1bit来编号就够了

停等协议-有差错情况

1. 数据帧丢失或检测到帧出错

设置的重传时间就是有一个超时计时器，每次发送一个帧就启动一个计时器。超时计时器设置的重传时间应当比帧传输的平均RTT（往返时延）更长一些

需要注意

1. 发完一个帧后，必须保留它的副本

2. 数据帧和确认帧必须编号

3. ACK丢失

3. ACK迟到

停等协议性能分析

信道利用率：发送方在一个发送周期内，有效的发送数据所需要的时间占整个发送周期的比率
$$信道利用率=\frac{L/C}{T}$$
T指发送周期，即从开始发送数据，到收到第一个确认帧为止，L指T内发送L比特的数据，单位比特，C值发送方数据传输率，单位比特/秒

信道利用率
$$U=\frac{T_D}{T_D+RTT+T_A}$$

信道吞吐率
$$信道吞吐率=信道利用率\times 发送发的发送速率$$

例：一个信道的数据利用率为4kb/s，单向传播时延为30ms，如果使停止-等待协议的信道最大利用率达到80%，要求数据帧的长度至少为
$$\begin{array}{rl}80\%& =\frac{L/4}{L/4+2\times 30ms}\\ L& =960bit\end{array}$$

后退N帧协议

滑动窗口相比于停等协议

1. 必须增加序号范围
2. 发送方需要缓存多个分组

发送窗口：发送方维持一组连续的允许发送的帧的序号
接收窗口：接收方维持一组连续的允许接收帧的序号

发送端每收到一个确认帧，发送窗口就向前滑动一个帧的位置，当发送窗口内没有可以发送的帧（即窗口内的帧全部是已发送但未收到确认的帧）时，发送方就会停止发送，直到收到接收方发送的确认帧使窗口移动，窗口内有可以发送的帧后，才开始继续发送。
接收端收到数据帧后，将窗口向前移一个位置，并发回确认帧，若收到的数据帧落在接收窗口之外，则一律丢弃。

停止等待协议可以看做特殊的滑动窗口协议，也就是发送窗口大小=1，接收窗口大小=1
后退N帧协议（GBN）发送窗口大小>1，接收窗口大小=1
选择重传协议（SR）发送窗口大小>1，接收窗口大小>1

后退N帧协议中的滑动窗口

相比于停等协议，后退N帧协议的接收窗口可以依次接收012甚至更多个帧，然后再发送一个ACK2（对应前面的012），这是发送窗口收到就可以向前移动3帧

GBN发送方必须响应的三件事

• 上层的调用

上层要发送数据时，发送方先检查发送窗口是否已满，如果未满，则产生一个帧并将其发送：如果窗口已满发送方只需将数据返回给上层，暗示上层窗口己满。上层等一会再发送。（实际实现中，发送方可以缓存这些数据，窗口不满时再发送帧）

• 收到了一个ACK

GBN协议中，对n号帧的确认采用累积确认的方式，标明接收方已经收到n号帧和它之前的全部帧。

• 超时事件

协议的名字为后退N帧/回退N帧，来源于出现丢失和时延过长帧时发送方的行为。就像在停等协议中一样，定时器将再次用于恢复数据帧或确认帧的丢失。如果出现超时，发送方重传所有己发送但未被确认的帧。

GBN接收方要做的事

如果正确收到n号帧，并且按序，那么接收方为n帧发送一个ACK，并将该帧中的数据部分交付给上层

其余情况都丢弃帧，并未最近按序接收的帧重新发送ACK。接收方无需缓存任何失序帧，只需要维护一个信息：expectedseqnum（下一个按序接受收的帧序号）

运行中的GBN

这里我们假设发送窗口尺寸为4。出现超时，发送方重传所有已发送但未被确认的帧

例如汉堡从上至下为面包片、芝士、西红柿、牛排、面包片，发送方从上到下一片一片的给接收方，接收方必须要按照从上至下的顺序吃，因此吃了面包片、芝士之后，如果来了牛排、面包，接收方都不吃，必须要西红柿

关于滑动窗口长度

若采用n个比特对帧编号，那么发送窗口的尺寸$W_T$应满足
$$1\le W_T\le 2^n-1$$
因为发送窗口尺寸过大，就会使得接收方无法区别新帧和旧帧
例如，如果我们对帧用2个比特编号，因此就可编号为0123，如果窗口为4，我们发完四个帧后，假设接收方的所有确认帧都丢失，那么此时超过计时器时间后，发送方再次发送0123，但是对于接收方而言，它无法判定这是这一次的0123，还是下一次的0123。因为如果按照0123的确认帧全部丢失，那么第二次收到的0123就应该是和前一次相同的，如果按照确认帧全部被正确收到，那么第二次收到的0123就应该是下一个0123，这对于接收方而言是无法判断的（也就是接收方无法判断是否发生了重传）。因此窗口最大只能为3

GBN协议重点总结

• 累计确认（偶尔捎带确认，这是对于假设A给B发送帧，但突然B需要给A发送帧，那么A可以把对B的确认帧打包在某一个发送数据的帧里面）
• 发送方只按顺序接收帧，不按序则丢弃
• 确认序列号最大的，按序到达的帧
• 发送窗口最大为$2^n-1$，接收窗口大小为1

GBN协议性能分析

连续发送数据帧而提高了信道利用率
在重传时必须把原来已经正确传送的数据帧重传，使传送效率降低

例题：
主机甲与主机乙之间使用后退N帧协议(GBN)传输数据，甲的发送窗口尺寸为1000，数据帧长为1000字节信道带宽为100Mb/s，乙每收到一个数据帧立即利用一个短帧（忽略其传输延迟）进行确认，若甲、乙之间的单向传播时延是50ms，则甲可以达到的最大平均数据传输率约为（）。
A.10Mb/s B.20Mb/s C.80Mb/s D.100Mb/s
$$\begin{array}{rl}\frac{1000\times 1000\times 8b}{1000\times 10^{6}b/s}& =80ms\end{array}$$
发送完所有窗口的帧需要80ms，如果窗口一直滑动，也就是一直有帧在发送，那么信道带宽就为数据传输率
$$\begin{array}{rl}2\times 50ms+\frac{1000\times 8b}{100\times 10^{6}b/s}& =100.08ms\end{array}$$
验证是否在发完一个窗口的最后一帧之前，能接收到第一帧的确认信息，但是显然收不到，因此发送$1000\times 1000\times 8b$的数据所需的时间大概是$100ms$，有
$$\begin{array}{rl}\frac{1000\times 1000\times 8b}{100.08ms}& \approx 80Mb/s\end{array}$$

选择重传协议

选择重传协议中的滑动窗口

SR发送方必须响应的三件事

• 上层的调用

从上层收到数据后，SR发送方检查下一个可用于该帧的序号，如果序号位于发送窗口内，则发送数据帧：否则就像GBN一样，要么将数据缓存，要么返回给上层之后再传输。

• 收到了一个ACK

如果收到ACK，加入该帧序号在窗口内，则SR发送方将那个被确认的帧标记为已接收。如果该帧序号是窗口的下界（最左边第一个窗口对应的序号），则窗口向前移动到具有最小序号的未确认帧处。如果窗口移动了并且有序号在窗口内的未发送帧，则发送这些帧。

• 超时事件

每个帧都有自己的定时器，一个超时事件发生后只重传一个帧

SR接收方要做的事

SR接收方将确认一个正确接受的帧而不管其是否按序。失序的帧将被缓存，并返回给一个该帧的确认帧（收谁确认谁），知道所有帧（即序号更小的帧）都被接收为止，这是才可以将一批帧按序交付给上层，然后向前移动滑动窗口

如果收到了窗口序号外（小于窗口下界）的帧，就返回一个ACK

其他情况忽略该帧

运行中的SR

滑动窗口长度

这里ACK012丢失，但实际上这里接收方收到的0号帧不知道是哪一个，有歧义，如下图

这里3号帧丢失
这两种情况下都能收到0号帧，但是分不清新帧和旧帧

发送窗口最好等于接收窗口（大了会溢出，小了没意义）

设帧的序号需要n个比特储存
$$W_{Tmax}=W_{Rmax}=2^{n-1}$$
$W_{Tmax},W_{Rmax}$分别是发送、接收窗口最大值

SR协议重点总结

• 对数据帧注意确认，收一个确认一个
• 只重传出错的帧
• 接收方有缓存
• $W_{Tmax}=W_{Rmax}=2^{n-1}$

例：
数据链路层采用了选择重传协议，发送发已经发送了0123号帧，现已收到1号帧确认，而02号帧依次超时，则发送方需要重传的帧数是（）
2，只有超时才需要重传，这里3不需要重传，因为没有超时，有可能只是还没收到，在路上

差错控制

概括来说，传书中的差错都是由于噪声引起的

• 全局性，由于线路本身电气特性所产生的随机噪声（热噪声），是信道固有的，随机存在的
  解决方法：提高信噪比来减少或避免干扰（对传感器下手）
• 局部性，外界特定的短暂原因所造成的冲击噪声，是产生差错的主要原因
  解决方法：通常利用编码技术解决

差错分为

• 位错：比特位出错，如1变成0，0变成1。本节只讨论位错
• 帧错：原本帧的顺序为(#1)-(#2)-(#3)
  • 丢失：收到(#1)-(#3)
  • 重复：收到(#1)-(#2)-(#2)-(#3)
  • 失序：收到(#1)-(#3)-(#2)

之前说到链路层为网络层提供服务有无确认无连接的服务，常用于通信质量好的有线传输链路；有确认无连接服务、有确认面向连接服务，常用于通信质量差的无线传输链路

差错控制主要分为：

• 检错编码：
  • 奇偶校验码
  • 循环冗余码CRC
• 纠错编码：海明码

数据链路层编码和物理层编码
数据链路层编码和物理层的数据编码与调制不同。物理层编码针对的是单个比特，解决传输过程中比特的同步等问题，如曼彻斯特编码。而数据链路层的编码针对的是一组比特，它通过见余码的技术实现一组二进制比特串在传输过程是否出现了差错。

检错编码

检错编码都采用冗余编码技术
冗余编码：在有效数据/信息位发送之前，先按某种关系附加上一定的冗余位，构成一个符合某一规则的码字后再发送。当要发送的有效数据变化时，相应的冗余位也随之变化，使码字遵从不变的规则。接收端根据收到码字是否仍符合原规则，从而判断是否出错
简单来说，就是在发送数据的时候不仅发送原始数据，同时在原始数据后面还有附加上几位比特，这几位比特就叫做冗余码，它的作用就是和原始数据可以构成某种规则，把这个组合发出去之后，接收方就按照和发送方共识的规则来检查是不是有问题，如果发现不符合这个规则就是有问题，反之无问题，接收
例如要发一串烧烤，在烧烤的首端加一块肉，告诉接收方，加上这块肉一共有偶数块肉，此时如果接收方发现肉是奇数块，则说明烧烤有问题

常见的检错编码有奇偶校验码和循环冗余码。

奇偶校验码

奇偶校验码由n-1位信息元和1位校验元组成
分为

• 奇校验码：在附加一个校验元后，码长为”的码字中“1”的个数为奇数
• 偶校验码：在附加一个校验元以后，码长为”的码字中“1”的个数为偶数。

特点：它只能检测奇数个比特的出错情况，但不能发现偶数个比特的出错情况，也并不知道哪些位错了。

CRC循环冗余码

操作方法

1. 准备带传的有效数据，并分成多组

2. 每个组都加上冗余码构成帧再发送。
   给定个m bit的领或报文，发送器生成一个r bit的序列，称为帧检验序列(FCS)。这样所形成的帧将由m+r比特组成。发送方和接收方事先商定一个生成多项式G(x)（最高位和最低位必须为1），使这个带检验码的帧刚好能被预先确定的多项式G(x)整除。

   这里生成多项式是r+1位的，已知条件会给到，不需要计算。如果最高位是0自动舍去不看，从第一个1开始，位数为r+1位。有时也用类似于
   $$x^4+x^2+x$$
   补全即为
   $$1\cdot x^4+0\cdot x^3+1\cdot x^2+1\cdot x+0$$
   对应生成多项式即为10110

   假设一个帧有m位，其对应的多项式为M(x)，则计算冗余码的步骤如下

   1. 加0。假设G(x)的阶为r，在帧的低位端加上r个0
   2. 模2除。利用模2法，用G(x)对应的数据串去除第一步中计算出的数据串，得到的余数即为冗余码（共r位，前面的0不可省略）
      模2法类似于异或，即异1同0。计算的时候注意，我们不关心商，算出余数就行

   

3. 接收方用相同的多项式去除收到的帧，如果无余数，那么认为无差错，正确接收；反之，丢弃

例：要发送的数据是1101 0110 11，采用CRC校验，生成多项式是10011，那么最终发送的数据应该是？
10011为生成多项式，因此冗余码有4位，加0后为11010110110000

FCS的生成以及接收端CRC检验都是由硬件实现，处理很迅速，因此不会延误数据的传输

链路层使用CRC检验，能够实现无比特差错传输，但这还不是可靠传输（因为有帧被丢弃）

纠错编码

之前的奇偶校验码和循环冗余码都是在最低位加，但海明码插入规则不同

海明距离：

• 两个合法编码（码字）的对应比特取值不同的比特数称为这两个码字的海明距离（码矩）
  000、011海明距离为2
• 一个有效编码集中，任意两个合法编码（码字）的海明距离的最小值称为该编码集的海明距离（码矩）
  000、001、111，编码集的海明距离为1

显然

• 如果编码系统中码矩为1，无法检错与纠错
  因为此时，任何一个码字出现1位错，因为码矩为1，也就是说会变成另一个码字，因此无法检错，从而无法纠错
• 如果编码系统中码矩为2，可以检错1位错，但无法纠错
  因为此时，任何一个码字出现1位错，因为码矩为2，也就是说错误的码字码矩为1，我们能够根据码矩1<2判断其出错了，但不知道它原本的码字，因为它到所有其他码字的距离都为1，任何码字变化1个数字都能变为错误的码字
• 如果编码系统中码矩为3，可以检错1、2位错，可以纠错1位错
  因为此时，任何一个码字出现1位错，因为码矩为3，也就是说错误的码字码矩为2，其与正确码字的码矩为1，与其他码字码矩为2，又因为只有一位错，因此可以纠错

总结：如果海明码要检测d位错，则海明矩为d+1；如果海明码纠正d位错，则海明矩为2d+1

海明码编码过程

1. 确定校验码位数r
   数据/信息有m位，冗余码/校验码有r位，因此校验码一共有$2^r$种取值，有海明不等式
   $$2^r\ge m+r+1$$
   例如我们现在有数据1100，可以算得r=3

2. 确定校验码和数据的位置
   校验码放在序号为$2^n$的位置，数据按序填上
   

3. 求出校验码的值
   

   4号校验码可以匹配类似1**的二进制位，这里的二进制位就是把序号用二进制表示。因此4号负责4567的校验，如果我们采用偶校验有?011，显然4号为0
   2号校验码可以匹配类似*1*的二进制位，因此2号负责2367的校验，如果采用偶校验有?011，显然2号为0
   1号校验码可以匹配类似**1的二进制位，因此1号负责1357的校验，如果采用偶校验有?001，显然1号为1
   得到完整海明码为
   

4. 检错并纠错
   

   用421分别进行偶校验即可
   如果我们收到的数据有问题，例如变为1110001
   4、1号校验发现有问题，2号校验无问题

   • 纠错方法一：找到不满足奇偶校验的分组取交集，并与符合校验的分组取差集，可以发现是5号出错
   • 纠错方法二：根据校验规则我们可以得到类似矩阵的式子，每一行是每一个校验码负责的码，对应本例为
     $$\left[\begin{array}{cccc}0& 1& 1& 1\\ 0& 0& 1& 1\\ 1& 0& 1& 1\end{array}\right]$$
     每一行进行异或操作，例如第一行即为
     $$0\oplus 1\oplus 1\oplus 1=1$$
     这一行对应$x_4$，因此$x_4=1$，类似可以得出$x_2=0,x_1=1$，我们将$x_4,x_2,x_1$得到的值横着排，即
     $$101$$
     这个二进制对应序号为5，因此错误即为5