NLP学习笔记十一-word2vec模型
再介绍word2vec模型之前,我们需要先介绍一些背景知识。
我们只知道,NLP这一领域在ward2vec出现之前肯定也是有很大程度发展的,那么想要用将自然语言用计算机进行处理,进行计算,我们必须对自然语言进行数字转换,那在一些词向量编码没有出现之前,我们一般使用one-hot技术对文本进行编码,一般使对文本进行分词,或者分字符,然后进行编码,这样就可以将自然语言信息数字化,计算机就可以识别和处理,但是呢,很快人们就发现one-hot编码技术是有着很大缺陷的,比如如果我们的编码类别达到几万,几十万,那么每个编码元素的向量长度就会使几万,甚至几十万,这会很大程度上增加内存的开销和计算的开销,而且one-hot编码技术如果对词语进行编码不能体现词语之间的内在联系。
所以,人们开始寻找另一中自然语言编码方式,力求不仅可以使得编码向量长度不那么长,而且还可以体现编码元素至今的内在联系。
下面我们再介绍一个知识点:自然语言中的分布广泛性,分布广泛性这一概念提出可谓是使得自然语言领域发生了翻天覆地变化,基于这一理念,出现了很多的词语编码模型,word2vec模型也是由此而出,分布广泛性这一原理就是说,一个词语,具有其自身的固定内在含义,那么由于它本身的内在含义,所以它在句子中的用法也会是有所限制,他的分布是由规律的,每个词语只会分布在有限的语境中,且分布是有规律的。
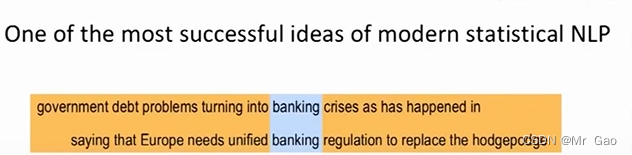
比如如下,banking,它的分布,每个词语,上下文不会是任意的,因为其自身含义的影响,上下文也是有规律的。
在介绍word2vec-skip-gram模型
skip-gram模型其实是一个概率模型,skip-gram模型给定它一个文本数据集,在给他一个窗口参数m,会得到每个文本中单词的词向量。
我们来看一下,skip-gram模型的的计算示意图:
: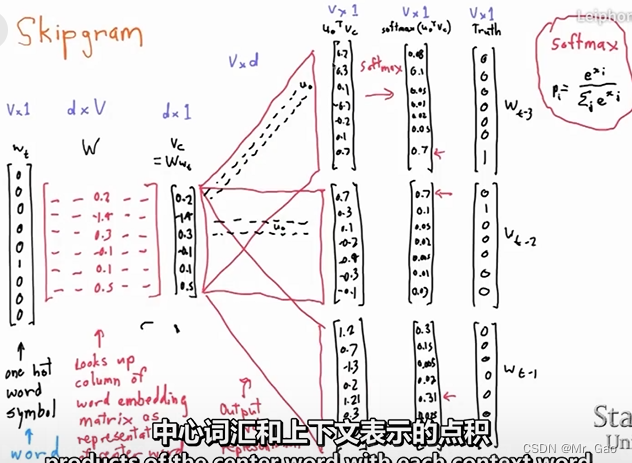
skip-gram模型基本用上面这张图就可以描述出来,上面这图是什么意思呢?
skip-gram模型输入的一个词语序列如下:
[
w
t
−
m
,
w
t
−
m
−
1
,
.
.
.
.
,
w
t
,
.
.
.
.
w
t
+
m
−
1
,
w
t
+
m
]
[w_{t-m},w_{t-m-1},....,w_{t},....w_{t+m-1},w_{t+m}]
[wt−m,wt−m−1,....,wt,....wt+m−1,wt+m]。
首先,我们知道,skip-gram模型的输入是什么呢,是一个词语序列,比如那么每个词语肯定不能直接做计算机的,需要先进性数字编码,我们还得用到one-hoe编码:
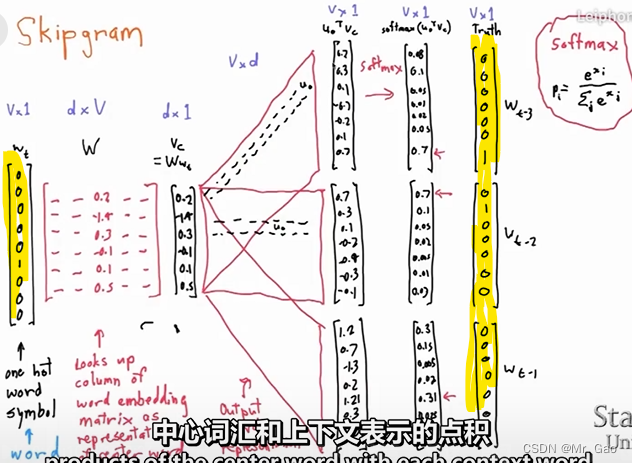
如上图啊,我标黄的就是我们的one-hot编码的部分:
就是对我们输入的一个文本序列进行one-hot编码:
[
w
t
−
m
,
w
t
−
m
−
1
,
.
.
.
.
,
w
t
,
.
.
.
.
w
t
+
m
−
1
,
w
t
+
m
]
[w_{t-m},w_{t-m-1},....,w_{t},....w_{t+m-1},w_{t+m}]
[wt−m,wt−m−1,....,wt,....wt+m−1,wt+m]。
编码完之后,
w
t
w_{t}
wt作为输入,乘以一个词向量表示矩阵,就是,
w
t
w_{t}
wt是一个01向量嘛,然后将它乘以一个矩阵,其实会把这个矩阵的某一行列出来,这一列其实也就是我们最后提取出的词向量表示,然后呢,我们把这个词向量在乘以2m 个mxn 的矩阵在进行softmax转化,是不是分别得到了2m个 1xn的向量。
注意:n就是输入数据集词语的类别个数。
那其实这2m个 1xn的向量 对应的就是他的上下文预测序列,向量中最大值对应的索引,该索引对应的单词即为预测的背景词汇。
注意:上面的2m 个mxn 矩阵都是同一个矩阵,所以这里也是博主很疑惑的一点,想了很久也没想通,每个位置的背景词汇按理不应该一样啊,但是,他用的确实同一个矩阵,所以skip-gram模型是有一个很大的问题的,他其实在论文中标识除了上下文位置的区分度,也就是上下文词汇是有位置去别的,但是这个模型在真正处理的时候,把上下文的词汇忽略了位置因素,相当于看成了一个集合,所以2m 个mxn 矩阵都是同一个矩阵。这才是正解,但是我看了很多资料很多人都只是浅浅的理解了一下这个模型。
注意:skip-gram模型其实并没有将上下文词汇位置的因素考虑进模型中。