⭐️前言⭐️
本篇文章是从暴力递归到动态规划篇目的最后一篇文章,包含了几道题目还有最终的大总结,相信这篇文章能让各位读者对动态规划有更深一步的了解。
🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁
🍉博主将持续更新学习记录收获,友友们有任何问题可以在评论区留言
🍉博客中涉及源码及博主日常练习代码均已上传GitHub

📍内容导读📍
- 🍅砍怪兽
- 🍅最少货币数
- 🍅拆分数字
- 🍅数组拆分
- 🍅数组拆分2
- 🍅贴纸拼词
- 🍅总结
🍅砍怪兽
题目:
给定3个参数,N,M,K
怪兽有N滴血,等着英雄来砍自己
英雄每一次打击,都会让怪兽流失[0~M]的血量
到底流失多少?每一次在[0~M]上等概率的获得一个值
求K次打击之后,英雄把怪兽砍死的概率
题解思路1:
总的情况数为(M+1)^k,通过暴力递归求出砍死怪兽的情况数,即可得到把怪兽砍死的概率。
递归终止的条件:
当次数为0时,看剩余血量,如果血量小于等于0,则返回1(说明是一种情况)
当血量为0时,剩余的次数都是能够砍死怪兽的情况,直接返回(M+1)^ times即为该情况下的所有情况数。
其余情况递归,根据0~M 血量的变化,进入不同的递归,记录不同的递归的情况数,求得最后的结果。
代码实现:
public class KillMonster {
public static double right(int N,int M,int K) {
if(N<1 || M<1 || K<1) {
return 0;
}
long all=(long) Math.pow(M+1,K);
long kill=process(K,M,N);
return (double) ((double)kill/(double) all);
}
// 怪兽还剩hp点血
// 每次的伤害范围为0~M
// 还有times可以砍
// 返回砍死的情况数
public static long process(int times,int M,int hp) {
if (times == 0) {
return hp <= 0 ? 1 : 0;
}
if(hp<=0) {
return (long) Math.pow(M+1,times);
}
long ways=0;
for (int i = 0; i <=M ; i++) {
ways+=process(times-1,M,hp-i);
}
return ways;
}
}
题解思路2:
根据暴力递归来转化为动态规划解法,由于有两个可变参数,所以可以通过构建一个二维DP表来存储不同剩余次数、不同血量时的情况数,最后返回表中需要位置的结果即可。
(注意:当血量为负的时候,把怪兽砍死的结果数就是(M+1)^(times-1))
代码实现:
public class KillMonster {
public static double dp1(int N,int M,int K) {
if(N<1 || M<1 || K<1) {
return 0;
}
long all=(long) Math.pow(M+1,K);
long[][] dp=new long[K+1][N+1];
dp[0][0]=1;
for (int times = 1; times <=K ; times++) {
dp[times][0]=(long) Math.pow(M+1,times);
for (int hp = 1; hp <=N ; hp++) {
long ways=0;
for (int i = 0; i <=M ; i++) {
if(hp-i>=0) {
ways+=dp[times-1][hp-i];
}else { // 当血量为负的时候,情况数直接就是下边的公式
ways+=(long) Math.pow(M+1,times-1);
}
}
dp[times][hp]=ways;
}
}
long kill=dp[K][N];
return (double) ((double)kill/(double) all);
}
}
题解思路3:
由于在求每个位置的dp结果时,存在for循环的枚举依赖,所以可以通过严格依赖的表结构关系进行优化,不使用枚举依赖。
代码实现:
public class KillMonster {
// 枚举优化
public static double dp2(int N,int M,int K) {
if(N<1 || M<1 ||K<1) {
return 0;
}
long all=(long) Math.pow(M+1,K);
long[][] dp=new long[K+1][N+1];
dp[0][0]=1;
for (int times = 1; times <=K ; times++) {
dp[times][0]=(long) Math.pow(M+1,times);
for (int hp = 1; hp <=N ; hp++) {
dp[times][hp]=dp[times][hp-1]+dp[times-1][hp];
if(hp-1-M>=0) {// 没有越界
dp[times][hp]-=dp[times-1][hp-1-M];
}else {// 如果越界了说明血量为负,也得减去情况数
dp[times][hp]-=Math.pow(M+1,times-1);
}
}
}
long kill=dp[K][N];
return (double) ((double)kill/(double) all);
}
}
🍅最少货币数
题目:
arr是面值数组,其中的值都是正数且没有重复。再给定一个正数aim。
每个值都认为是一种面值,且认为张数是无限的。
返回组成aim的最少货币数
题解思路:
从左往右的尝试模型,依次考虑每个面值对应不同数的情况,记录能够组成aim的最小张数返回即可。
代码实现:
public class MinCoinsNoLimit {
public static int minCoins(int[] arr,int aim) {
return process(arr,0,aim);
}
// arr[index...]面值,每种面值张数自由选择
// 凑出正好rest的钱数,返回最小张数
// 拿Integer.MAX_VALUE标记怎样也凑不出
public static int process(int[] arr,int index,int rest) {
if(index==arr.length) {
return rest==0?0:Integer.MAX_VALUE;
}else {
int ans=Integer.MAX_VALUE;
for (int pages = 0; pages*arr[index] <=rest ; pages++) {
int next=process(arr,index+1,rest-pages*arr[index]);
if(next!=Integer.MAX_VALUE) {
ans=Math.min(ans,next+pages);
}
}
return ans;
}
}
}
题解思路2:
根据暴力递归转化为动态规划,由于有两个可变参数,所以可以依此构建一个二维dp表,记录不同面值,不同rest,再根据index+1位置面值的不同张数返回的情况数,取最小结果填入。
代码实现:
public class MinCoinsNoLimit {
public static int dp1(int[] arr,int aim) {
if(aim==0) {
return 0;
}
int N=arr.length;
int[][] dp=new int[N+1][aim+1];
dp[N][0]=0;
for (int j = 1; j <=aim ; j++) {
dp[N][j]=Integer.MAX_VALUE;
}
for (int index = N-1; index >=0 ; index--) {
for (int rest = 0; rest <=aim ; rest++) {
int ans=Integer.MAX_VALUE;
for (int pages = 0; pages*arr[index] <=rest ; pages++) {
int next=dp[index+1][rest-pages*arr[index]];
if(next!=Integer.MAX_VALUE) {
ans=Math.min(ans,pages+next);
}
}
dp[index][rest]=ans;
}
}
return dp[0][aim];
}
}
题解思路3:
由于每个位置的填写,都依赖于枚举得到的结果,所以可以根据严格依赖的表结构位置关系,优化枚举行为。
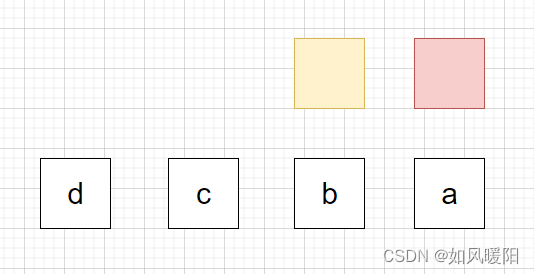
红色方格的值依赖于Math.min(a+0,b+1,c+2,d+3) 【最后加几取决于rest,只要不越过左边界即可】
黄色方格的值依赖于Math.min(b+0,c+1,d+2)
所以dp[index][rest]=Math.min(dp[index+1][rest],dp[index][rest-arr[index]]+1)
代码实现:
public class MinCoinsNoLimit {
public static int dp2(int[] arr,int aim) {
if(aim==0) {
return 0;
}
int N=arr.length;
int[][] dp=new int[N+1][aim+1];
dp[N][0]=0;
for (int j = 1; j <=aim ; j++) {
dp[N][j]=Integer.MAX_VALUE;
}
for (int index = N-1; index >=0 ; index--) {
for (int rest = 0; rest <=aim ; rest++) {
dp[index][rest]=dp[index+1][rest];
if(rest-arr[index]>=0&&
dp[index][rest-arr[index]]!=Integer.MAX_VALUE) {
dp[index][rest]=Math.min(dp[index][rest-arr[index]]+1,dp[index][rest]);
}
}
}
return dp[0][aim];
}
}
🍅拆分数字
题目:
给定一个正数n,求n的裂开方法数,
规定:后面的数不能比前面的数小
比如4的裂开方法有:
1+1+1+1、1+1+2、1+3、2+2、4
5种,所以返回5
题解思路1:
如果想要拆分5,就假设拆分6,先拆成了1和5,看5剩下多少种拆分办法。
base case:当rest剩余0时,说明完全拆分完成,则返回一种情况,如果pre>rest,则不符合条件,返回0。
代码实现:
public class SplitNumber {
// n为正数
public static int ways(int n) {
if(n<0) {
return 0;
}
if(n==1) {
return 1;
}
return process(1,n);
}
// 上一个拆出来的数是pre
// 还剩rest需要去拆
// 返回拆解的方法数
public static int process(int pre, int rest) {
if(rest==0) {
return 1;
}
if(pre>rest) {
return 0;
}
int ways=0;
for (int first = pre; first <=rest ; first++) {
ways+=process(first,rest-first);
}
return ways;
}
}
题解思路2:
由暴力递归转化为动态规划,有两个可变参数pre和rest,先跟base case完成部分位置的填写,再根据暴力递归的依赖关系,来推断出dp表中其他位置该如何填写。
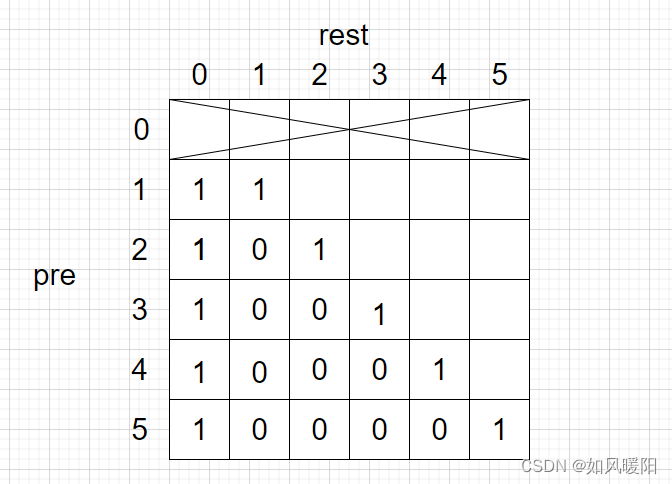
代码实现:
public class SplitNumber {
public static int dp1(int n) {
if(n<0) {
return 0;
}
if(n==1) {
return 1;
}
int[][] dp=new int[n+1][n+1];
for (int pre = 1; pre <=n ; pre++) {
dp[pre][0]=1;
dp[pre][pre]=1;
}
for (int pre = n-1; pre >=0 ; pre--) {
for (int rest = pre+1; rest <=n ; rest++) {
int ways=0;
for (int first = pre; first <=rest ; first++) {
ways+=dp[first][rest-first];
}
dp[pre][rest]=ways;
}
}
return dp[1][n];
}
}
题解思路3:
由于每个位置的填写有枚举依赖,所以可以根据严格依赖的位置关系再做优化,对枚举行为进行优化。
dp[pre][rest]=dp[pre+1][rest]+dp[pre][rest-pre]

代码实现:
public class SplitNumber {
public static int dp2(int n) {
if(n<0) {
return 0;
}
if(n==1) {
return 1;
}
int[][] dp=new int[n+1][n+1];
for (int pre = 1; pre <=n ; pre++) {
dp[pre][0]=1;
dp[pre][pre]=1;
}
for (int pre = n-1; pre >=0 ; pre--) {
for (int rest = pre+1; rest <=n ; rest++) {
dp[pre][rest]=dp[pre+1][rest];
dp[pre][rest]+=dp[pre][rest-pre];
}
}
return dp[1][n];
}
}
🍅数组拆分
题目:
给定一个正数数组arr,
请把arr中所有的数分成两个集合,尽量让两个集合的累加和接近
返回最接近的情况下,较小集合的累加和
题解思路1:
从左往右的尝试模型,每个位置都有要或者不要两种情况,递归就是返回接近于rest但不大于rest的最大累加和。
代码实现:
public class SplitSumClosed {
public static int right(int[] arr) {
if(arr==null||arr.length<2) {
return 0;
}
int sum=0;
for(int num:arr) {
sum+=num;
}
return process(arr,0,sum/2);
}
// arr[i...]可以自由选择,返回累加和尽量接近rest,但不能超过rest的情况下,最接近的累加和是多少
public static int process(int[] arr,int i,int rest) {
if(i==arr.length) {
return 0;
}else { // 还有数
// 可能性1,不使用arr[i]
int p1=process(arr,i+1,rest);
// 可能性2,使用arr[i]
int p2=0;
if(arr[i]<=rest) {
p2=arr[i]+process(arr,i+1,rest-arr[i]);
}
return Math.max(p1,p2);// 返回两种可能性中更接近的
}
}
}
题解思路2:
暴力递归中有两个可变参数,所以可以优化为一个二维dp表,来进行存储不同状态下的结果,根据位置依赖关系来填写dp表,最后返回所需要状态的结果。
代码实现:
public class SplitSumClosed {
public static int dp(int[] arr) {
if(arr==null||arr.length<2) {
return 0;
}
int sum=0;
for (int num:arr) {
sum+=num;
}
sum/=2;
int N=arr.length;
int[][] dp=new int[N+1][sum+1];
for (int i = N-1; i >=0 ; i--) {
for (int rest = 0; rest <=N ; rest++) {
// 可能性1,不使用arr[i]
int p1=dp[i+1][rest];
// 可能性2,使用arr[i]
int p2=0;
if(arr[i]<=rest) {
p2=arr[i]+dp[i+1][rest-arr[i]];
}
dp[i][rest]= Math.max(p1,p2);
}
}
return dp[0][sum];
}
}
🍅数组拆分2
题目:
给定一个正数数组arr,请把arr中所有的数分成两个集合
如果arr长度为偶数,两个集合包含数的个数要一样多
如果arr长度为奇数,两个集合包含数的个数必须只差一个
请尽量让两个集合的累加和接近
返回最接近的情况下,较小集合的累加和
题解思路1:
与数组拆分1类似,只不过加上了个数限制,要根据arr长度来决定集合中只能选几个数。
代码实现:
public class SplitSumClosedSizeHalf {
public static int right(int[] arr) {
if(arr==null||arr.length<2) {
return 0;
}
int sum=0;
for (int num:arr) {
sum+=num;
}
if((arr.length&1)==0) {
return process(arr,0,arr.length/2,sum/2);
}else {
return Math.max(process(arr,0,arr.length/2,sum/2),process(arr,0,arr.length/2+1,sum/2));
}
}
// arr[i...]自由选择,挑选的个数一定是picks个,累加和<=rest,离rest最接近的返回
public static int process(int[] arr, int i, int picks, int rest) {
if(i==arr.length) {
return picks==0?0:-1; // 不合法用-1标记
}else {
// 不用arr[i]
int p1=process(arr, i+1, picks, rest);
// 用arr[i]
int p2=-1;
int next=-1;
if(arr[i]<=rest) {
next=process(arr,i+1,picks-1,rest-arr[i]);
}
// 如果下一层有效
if(next!=-1) {
p2=arr[i]+next;
}
return Math.max(p1,p2);
}
}
}
题解思路2:
根据暴力递归的三个可变参数,建立一个三维的dp表,根据位置依赖关系填写dp表,最后返回所要位置的dp结果。
代码实现:
public class SplitSumClosedSizeHalf {
public static int dp(int[] arr) {
if(arr==null||arr.length<2) {
return 0;
}
int sum=0;
for (int num:arr) {
sum+=num;
}
sum/=2;
int N=arr.length;
int M=(N+1)/2;// 向上取整
int[][][] dp=new int[N+1][M+1][sum+1];
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= M; j++) {
for (int k = 0; k <= sum; k++) {
dp[i][j][k] = -1;
}
}
}
for (int rest = 0; rest <=sum ; rest++) {
dp[N][0][rest]=0;
}
for (int i = N-1; i >=0 ; i--) {
for (int picks = 0; picks <=M ; picks++) {
for (int rest = 0; rest <=sum ; rest++) {
// 不用arr[i]
int p1=dp[i+1][picks][rest];
// 用arr[i]
int p2=-1;
int next=-1;
if(arr[i]<=rest) {
next=dp[i+1][picks-1][rest-arr[i]];
}
// 如果下一层有效
if(next!=-1) {
p2=arr[i]+next;
}
dp[i][picks][rest]= Math.max(p1,p2);
}
}
}
if((arr.length&1)==0) {
return dp[0][arr.length/2][sum];
}else {
return Math.max(dp[0][arr.length/2][sum],dp[0][arr.length/2+1][sum]);
}
}
}
🍅贴纸拼词
题目:
给定一个字符串str,给定一个字符串类型的数组arr。
arr里的每一个字符串,代表一张贴纸,你可以把单个字符剪开使用,目的是拼出str来。
返回需要至少多少张贴纸可以完成这个任务。
例子:str= “babac”,arr = {“ba”,“c”,“abcd”}
至少需要两张贴纸"ba"和"abcd",因为使用这两张贴纸,把每一个字符单独剪开,含有2个a、2个b、1个c。是可以拼出str的。所以返回2。
https://leetcode-cn.com/problems/stickers-to-spell-word/
题解思路:
每张贴纸都可以作为第一张,如果该贴纸有效(即可以减掉部分字符),则递归进入下一层(传入的参数变为减后的字符串);如果该贴纸无效,则直接就是默认为系统最大值,最后返回记录的最小结果。
代码实现:
public class StickersToSpellWord {
public static int minSticker1(String[] stickers,String target) {
int ans=process(stickers,target);
return ans==Integer.MAX_VALUE?-1:ans;
}
// 所有贴纸stickers,每一种贴纸都有无穷张
// target
// 最少张数
public static int process(String[] stickers,String target) {
if(target.length()==0) {
return 0;
}
int min=Integer.MAX_VALUE;
for (String first:stickers) {
String rest=minus(target,first);
if(rest.length()!=target.length()) {
min=Math.min(min,process(stickers,rest));
}
}
return min+(min==Integer.MAX_VALUE?0:1);
}
public static String minus(String s1,String s2) {
char[] str1=s1.toCharArray();
char[] str2=s2.toCharArray();
int[] count=new int[26];
for (char ch:str1) {
count[ch-'a']++;
}
for (char ch:str2) {
count[ch-'a']--;
}
StringBuilder builder=new StringBuilder();
for (int i = 0; i < 26; i++) {
if(count[i]>0) {
for (int j = 0; j < count[i]; j++) {
builder.append((char) (i+'a'));
}
}
}
return builder.toString();
}
}
题解思路2:
可以将词频表和贴纸都转换为数组,在相减时可以直接数组相减。
代码实现:
public class StickersToSpellWord {
public static int minStickers2(String[] stickers,String target) {
int N=stickers.length;
// 关键优化(用词频表代替贴纸数组)
int[][] counts=new int[N][26];
for (int i = 0; i < N; i++) {
char[] str=stickers[i].toCharArray();
for (char ch:str) {
counts[i][ch-'a']++;
}
}
int ans=process2(counts,target);
return ans==Integer.MAX_VALUE?-1:ans;
}
// stickers[i]数组
// 每种贴纸都有无穷张
// 返回搞定target的最少张数
public static int process2(int[][] stickers,String t) {
if(t.length()==0) {
return 0;
}
// target做出词频统计
char[] target=t.toCharArray();
int[] tcounts=new int[26];
for (char ch:target) {
tcounts[ch-'a']++;
}
int N=stickers.length;
int min=Integer.MAX_VALUE;
for (int i = 0; i < N; i++) {
// 尝试第一张贴纸是谁
int[] sticker=stickers[i];
// 剪枝优化
if(sticker[target[0]-'a']>0) { // 如果目标target中的字符在该贴纸中存在
StringBuilder builder=new StringBuilder();
for (int j = 0; j < 26; j++) {
if(tcounts[j]>0) {
int nums=tcounts[j]-sticker[j];
for (int k = 0; k < nums; k++) {
builder.append((char) j+'a');
}
}
}
String rest=builder.toString();
min=Math.min(min,process2(stickers,rest));
}
}
return min+(min==Integer.MAX_VALUE?0:1);
}
}
🍅总结
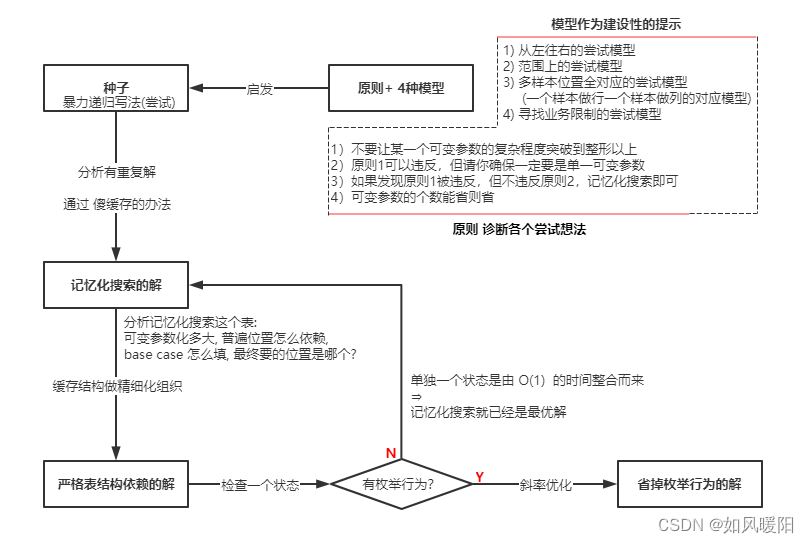
什么暴力递归可以继续优化?
有重复调用同一个子问题的解,这种递归可以优化;
如果每个子问题都是不同的解,无法优化也不用优化。
暴力递归和动态规划的关系
某一个暴力递归,有解的重复调用,就可以把这个暴力递归优化成动态规划
任何动态规划问题,都一定对应着某一个有解的重复调用的暴力递归
但不是所有的暴力递归,都一定对应着动态规划
常见的四种模型
1、从左往右的尝试模型
2、范围尝试模型
3、样本对应模型
4、业务限制模型
⭐️最后的话⭐️
总结不易,希望uu们不要吝啬你们的👍哟(^U^)ノ~YO!!如有问题,欢迎评论区批评指正😁