在本教程中，我们将更深入地了解如何将图神经网络（GNN）应用于图分类任务。图分类是指在给定图的数据集的情况下，基于一些结构图的属性对整个图（与节点相反）进行分类的问题。在这里，我们希望嵌入整个图，并且我们希望以这样一种方式嵌入这些图，即在手头有任务的情况下，它们是线性可分离的。

       图分类最常见的任务是分子性质预测，其中分子被表示为图，该任务可能是推断分子是否抑制HIV病毒复制。
       多特蒙德工业大学（The TU Dortmund University）收集了一系列不同的图分类数据集，称为TUDatasets，这些数据集也可以通过PyTorch Geometric中的torch_geometric.datasets.TUDataset 访问。让我们加载并检查其中一个较小的数据集，即MUTAG dataset：

import torch
from torch_geometric.datasets import TUDataset

dataset = TUDataset(root='data/TUDataset', name='MUTAG')

print()
print(f'Dataset: {dataset}:')
print('====================')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')

data = dataset[0]  # Get the first graph object.

print()
print(data)
print('=============================================================')

# Gather some statistics about the first graph.
print(f'Number of nodes: {data.num_nodes}')
print(f'Number of edges: {data.num_edges}')
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}')
print(f'Has isolated nodes: {data.has_isolated_nodes()}')
print(f'Has self-loops: {data.has_self_loops()}')
print(f'Is undirected: {data.is_undirected()}')

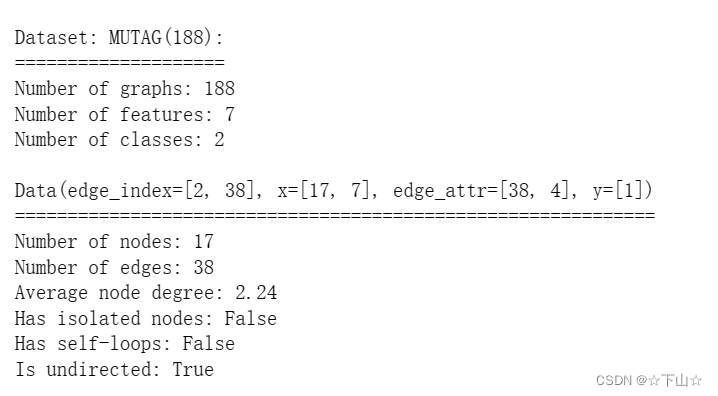
       该数据集提供了188个不同的图，任务是将每个图分类为两类中的一类。
       通过检查数据集的第一个图对象，我们可以看到它有17个节点（具有7维特征向量）和38条边（导致平均节点度为2.24）。它还只附带了一个图标签（y=[1]），并且除了以前的数据集之外，还提供了附加的4维边缘特征（edge_attr=[38，4]）。然而，为了简单起见，我们不会使用这些。
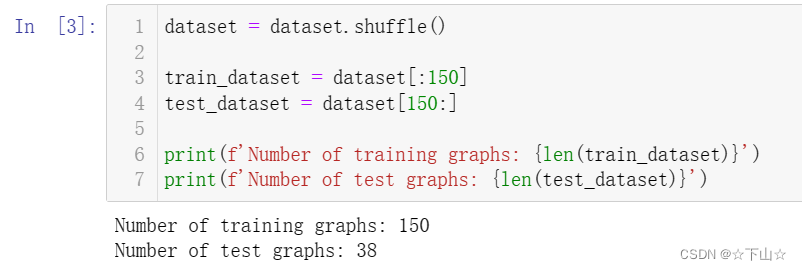
       PyTorch Geometric为处理图形数据集提供了一些有用的实用程序，例如，我们可以对数据集进行打乱，并使用前150个图形作为训练图，同时使用其余的图形进行测试：

图形的小型批处理

       由于图分类数据集中的图通常很小，因此一个好主意是在将图输入到图神经网络之前对图进行批处理，以确保GPU的充分利用。在图像或语言领域，此过程通常通过将每个示例重新缩放或填充为一组大小相等的形状来实现，然后将示例分组为附加维度。该维度的长度等于小批量中分组的示例数，通常称为batch_size。

       然而，对于GNN，上述两种方法要么不可行，要么可能导致大量不必要的内存消耗。因此，PyTorch Geometric选择了另一种方法来实现跨多个示例的并行化。这里，邻接矩阵以对角线的方式堆叠（创建一个包含多个孤立子图的巨型图），节点和目标特征在节点维度中简单地连接：

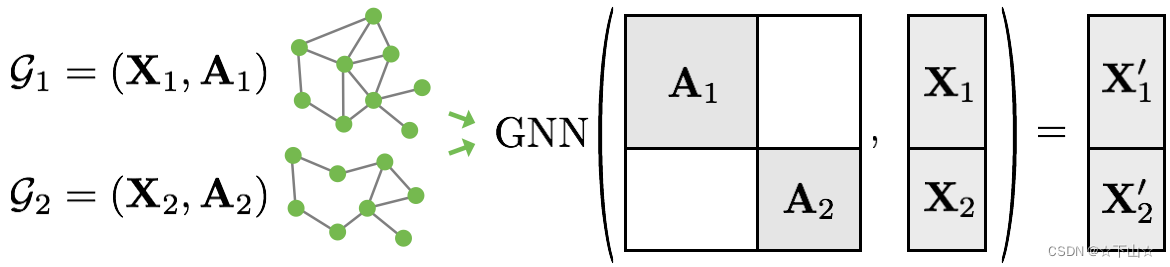
       与其它batching程序相比，该程序具有一些关键优势：

1. 依赖于消息传递方案的GNN运算符不需要修改，因为属于不同图的两个节点之间不交换消息。

2. 没有计算或内存开销，因为邻接矩阵是以稀疏的方式保存的，只包含非零条目，即边缘。

       通过torch_geometric.data.DataLoader 类，PyTorch Geometric自动将多个图批处理为单个巨型图 ：

from torch_geometric.loader import DataLoader

train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)

for step, data in enumerate(train_loader):
    print(f'Step {step + 1}:')
    print('=======')
    print(f'Number of graphs in the current batch: {data.num_graphs}')
    print(data)
    print()

       这里，我们设置batch_size 为64，3个 (随机打乱的) mini-batches，一共 $2\cdot 64+22=150$ 个图.

       此外，每个 Batch 对象搭配一个batch 矢量， 其将每个节点映射到该批中的其各自的图：

$$\text{batch}=[0,\dots ,0,1,\dots ,1,2,\dots ]$$

训练一个图神将网络（GNN）

训练用于图分类的GNN通常遵循一个简单的方案：

1. 通过执行多轮消息传递嵌入每个节点
2. 将节点嵌入聚合到统一图嵌入中 (readout layer)
3. 在图嵌入上训练最终分类器

文献中存在多个readout layer，但最常见的是简单地取节点嵌入的平均值：
$${\mathbf{x}}_{\mathcal{G}}=\frac{1}{|\mathcal{V}|}\sum _{v\in \mathcal{V}}{x}_v^{(L)}$$

       PyTorch Geometric通过torch_geometric.nn.global_mean_pool提供了该功能，其考虑小批处理中所有节点的节点嵌入和分配向量批处理，以针对批处理中的每个图计算大小为[batch_size, hidden_channels] 的图嵌入。

       将GNN应用于图分类任务的最终架构如下所示，并允许进行完整的端到端训练：

from torch.nn import Linear
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
from torch_geometric.nn import global_mean_pool


class GCN(torch.nn.Module):
    def __init__(self, hidden_channels):
        super(GCN, self).__init__()
        self.conv1 = GCNConv(dataset.num_node_features, hidden_channels)
        self.conv2 = GCNConv(hidden_channels, hidden_channels)
        self.conv3 = GCNConv(hidden_channels, hidden_channels)
        self.lin = Linear(hidden_channels, dataset.num_classes)

    def forward(self, x, edge_index, batch):
        # 1. Obtain node embeddings 
        x = self.conv1(x, edge_index)
        x = x.relu()
        x = self.conv2(x, edge_index)
        x = x.relu()
        x = self.conv3(x, edge_index)

        # 2. Readout layer
        x = global_mean_pool(x, batch)  # [batch_size, hidden_channels]

        # 3. Apply a final classifier
        x = F.dropout(x, p=0.5, training=self.training)
        x = self.lin(x)
        
        return x

model = GCN(hidden_channels=64)
print(model)

       在这里，在我们最终分类器应用于图形读出层的顶部之前，我们再次使用GCNConv ，用$\mathrm{ReLU}(x)=\max (x,0)$获得局部的节点嵌入激活。

       让我们对我们的网络进行几个时期的训练，看看它在训练和测试集上的表现如何：

model = GCN(hidden_channels=64)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
criterion = torch.nn.CrossEntropyLoss()

from torch_geometric.utils import to_networkx

def train():
    model.train()

    for data in train_loader:  # Iterate in batches over the training dataset.
        
        # G = to_networkx(data, to_undirected=True)
        # visualize_graph(G)
        
        out = model(data.x, data.edge_index, data.batch)  # Perform a single forward pass.
        loss = criterion(out, data.y)  # Compute the loss.
        loss.backward()  # Derive gradients.
        optimizer.step()  # Update parameters based on gradients.
        optimizer.zero_grad()  # Clear gradients.

def test(loader):
    model.eval()

    correct = 0
    for data in loader:  # Iterate in batches over the training/test dataset.
        out = model(data.x, data.edge_index, data.batch)  
        pred = out.argmax(dim=1)  # Use the class with highest probability.
        correct += int((pred == data.y).sum())  # Check against ground-truth labels.
    return correct / len(loader.dataset)  # Derive ratio of correct predictions.


for epoch in range(181):
    train()
    train_acc = test(train_loader)
    test_acc = test(test_loader)
    if epoch % 20 == 0:
        print(f'Epoch: {epoch:03d}, Train Acc: {train_acc:.4f}, Test Acc: {test_acc:.4f}')

       可以看出，我们的模型达到了大约84%的测试准确率。
       准确性波动的原因可以用相当小的数据集（只有38个测试图）来解释，并且一旦将GNN应用于较大的数据集，通常就会消失。

本文内容参考：PyG官网