一. 逆波兰表达式的介绍

逆波兰表达式又称为后缀表达式，代表的含义是操作数在前，运算符在后。

比如：1+2，用逆波兰表达式来写的话，就是12+。
而1+2这种写法称为中缀表达式，即运算符在两个操作数之间，也是我们平常最常采用的写法。

中缀表达式	逆波兰表达式
A+B	AB+
A*B	AB*
–	–
A+B*C	ABC*+
A*(B+C)	ABC*+
–	–

二. 逆波兰表达式的优点

逆波兰表达式的优点是可以把复杂表达式转换为可以依靠简单的操作得到计算结果的表达式。

只用两种简单操作：入栈和出栈，就可以搞定任何普通表达式的运算。

三. 逆波兰表达式的求值步骤

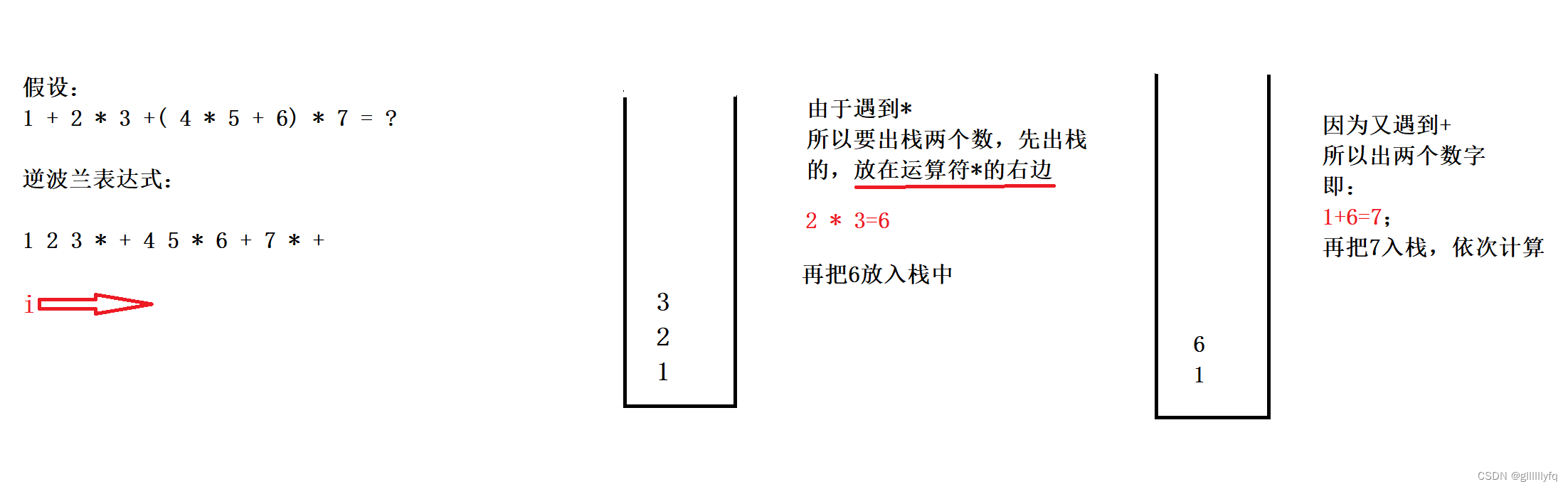
在这里插入图片描述

逆波兰式的求解过程可以用栈来实现。为了便于理解，举一个带数值的例子：

计算：1 + 2 * 3 + ( 4 * 5 +6 ) * 7 = ?
在这里插入图片描述

四. 例题—力扣

https://leetcode-cn.com/problems/evaluate-reverse-polish-notation/
在这里插入图片描述

4.1 解题思路

先建立一个栈，存放数据
一一遍历，当遍历的为数字的时候，放入栈中，
如果遇到运算符，则从栈中出两个数，先出的数，放运算符右边，计算完的结果，再次放入栈中，继续操作，遇到便数字压入栈中，遇到符号，弹出栈顶两元素并压入其结果。
直至结束

4.2 代码

class Solution {
     public int evalRPN(String[] tokens) {
        Stack<Integer> stack=new Stack<>();
        for(String s:tokens){
            if(!isO(s)){
            //数字 字符
            //用parseInt
                stack.push(Integer.parseInt(s));
            }
            else{
            //运算符
                int num2=stack.pop();
                int num1=stack.pop();//因为先出栈的是放运算符的右边，所以num1和num2的顺序很重要
                switch(s) {
                    case "+":
                        stack.push(num1 + num2);
                        break;
                    case "-":
                        stack.push(num1 - num2);
                        break;
                    case "*":
                        stack.push(num1 * num2);
                        break;
                    case "/":
                        stack.push(num1 / num2);
                        break;
                }
            }
        }
        return stack.pop();
    }
    //判断是否为运算符---isO
    private boolean isO(String s) {
        if(s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")) {
            return true;
        }
        return false;
    }