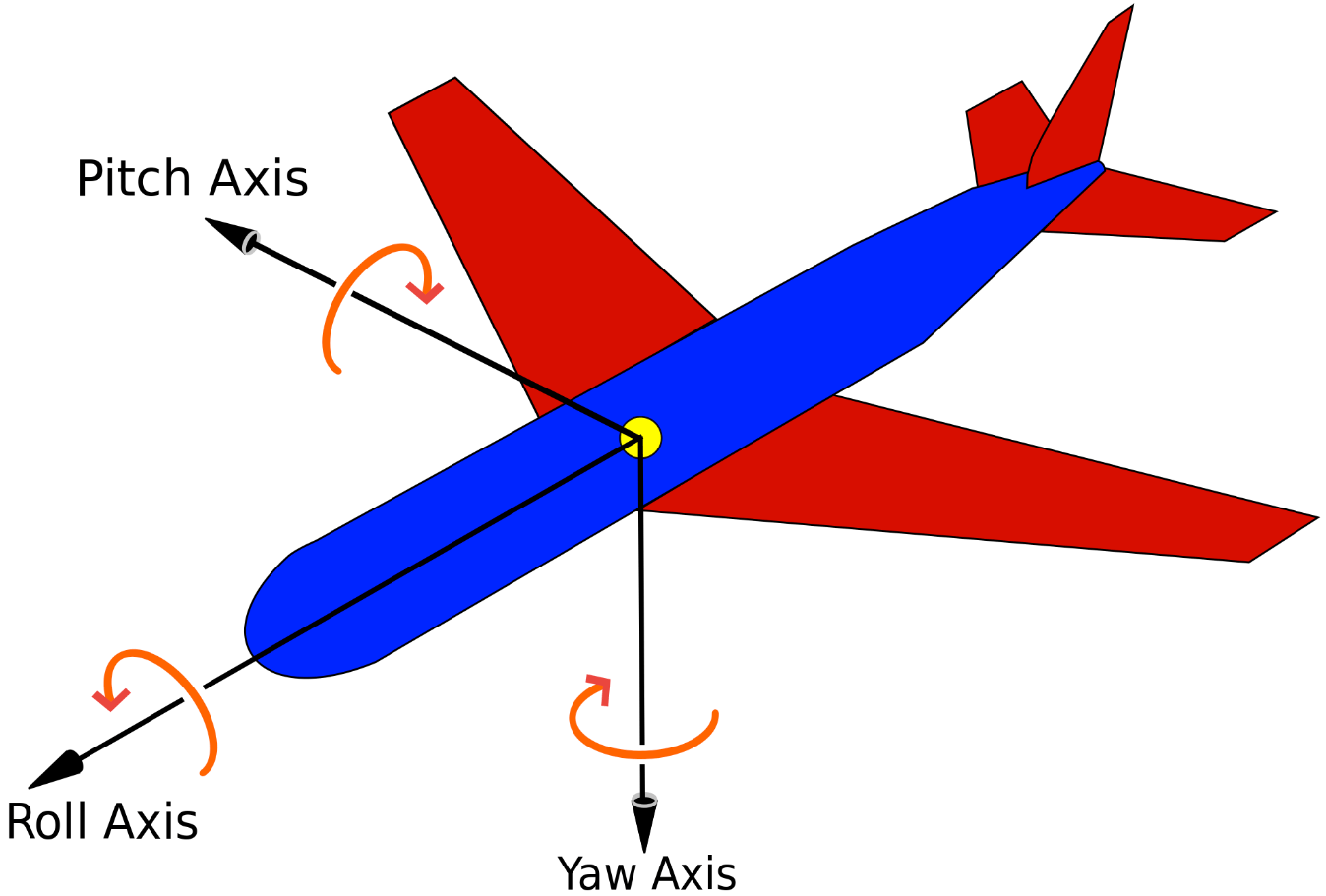
在飞行器的控制中，姿态计算是至关重要的一步。姿态计算的目标是确定飞行器相对于参考坐标系的姿态，通常以欧拉角（滚转、俯仰和偏航）或四元数的形式表示。

以下是姿态计算的原理和常用方法的简要介绍：

原理：
姿态计算基于惯性测量单元（IMU），其中包括加速度计和陀螺仪。加速度计测量物体在三个轴向上的加速度，而陀螺仪测量物体绕三个轴向上的角速度。通过结合这些测量值，可以推导出飞行器的姿态。

常用方法：

1. 互补滤波器（Complementary Filter）：这是一种简单且常用的姿态计算方法。它基于加速度计和陀螺仪的数据，通过加权平均来结合它们的优点。具体而言，加速度计用于低频信号（如重力）的测量，而陀螺仪用于高频信号（如旋转）的测量。通过调整加速度计和陀螺仪的权重，可以获得相对稳定的姿态估计。

2. 卡尔曼滤波器（Kalman Filter）：卡尔曼滤波器是一种更复杂但更精确的姿态估计方法。它基于状态估计和观测模型，并通过递归处理将测量数据与系统模型相结合。卡尔曼滤波器考虑了测量误差、系统噪声和先验信息，并通过最小化均方误差来优化姿态估计结果。这种方法对于高精度的姿态计算非常有效，但需要更复杂的数学推导和实现。

对于使用MPU6050作为传感器的实际案例，以下是一个简单的示例代码，演示如何使用MPU6050进行姿态计算：

import smbus
import math

# MPU6050的I2C地址
MPU6050_ADDR = 0x68

# 加速度计的灵敏度，根据MPU6050配置进行选择
ACCEL_SCALE = 16384.0

# 陀螺仪的灵敏度，根据MPU6050配置进行选择
GYRO_SCALE = 131.0

# 初始化I2C总线
bus = smbus.SMBus(1)

# 启动MPU6050传感器
bus.write_byte_data(MPU6050_ADDR, 0x6B, 0)

# 读取加速度计原始数据
def read_accel_data(addr):
    raw_data = bus.read_i2c_block_data(MPU6050_ADDR, addr, 6)
    accel_x = (raw_data[0] << 8) + raw_data[1]
    accel_y = (raw_data[2] << 8) + raw_data[3]
    accel_z = (raw_data[4] << 8) + raw_data[5]
    return (accel_x, accel_y, accel_z)

# 读取陀螺仪原始数据
def read_gyro_data(addr):
    raw_data = bus.read_i2c_block_data(MPU6050_ADDR, addr, 6)
    gyro_x = (raw_data[0] << 8) + raw_data[1]
    gyro_y = (raw_data[2] << 8) + raw_data[3]
    gyro_z = (raw_data[4] << 8) + raw_data[5]
    return (gyro_x, gyro_y, gyro_z)

# 计算加速度计的姿态
def calculate_accel_angles(accel_x, accel_y, accel_z):
    roll = math.atan2(accel_y, accel_z) * 180 / math.pi
    pitch = math.atan2(-accel_x, math.sqrt(accel_y * accel_y + accel_z * accel_z)) * 180 / math.pi
    return (roll, pitch)

# 计算陀螺仪的姿态
def calculate_gyro_angles(gyro_x, gyro_y, gyro_z, dt):
    roll = gyro_x * dt
    pitch = gyro_y * dt
    yaw = gyro_z * dt
    return (roll, pitch, yaw)

# 主循环
while True:
    # 读取加速度计数据
    accel_data = read_accel_data(0x3B)
    accel_x = accel_data[0] / ACCEL_SCALE
    accel_y = accel_data[1] / ACCEL_SCALE
    accel_z = accel_data[2] / ACCEL_SCALE

    # 读取陀螺仪数据
    gyro_data = read_gyro_data(0x43)
    gyro_x = gyro_data[0] / GYRO_SCALE
    gyro_y = gyro_data[1] / GYRO_SCALE
    gyro_z = gyro_data[2] / GYRO_SCALE

    # 计算加速度计的姿态
    accel_angles = calculate_accel_angles(accel_x, accel_y, accel_z)

    # 计算陀螺仪的姿态
    gyro_angles = calculate_gyro_angles(gyro_x, gyro_y, gyro_z, dt)

    # 结合加速度计和陀螺仪的姿态，使用互补滤波器或其他方法进行姿态计算

    # 输出姿态信息
    print("Roll: %.2f" % roll)
    print("Pitch: %.2f" % pitch)
    print("Yaw: %.2f" % yaw)

以上代码演示了如何使用MPU6050读取加速度计和陀螺仪的原始数据，并使用简单的角度计算函数来计算飞行器的姿态。你可以根据需要结合互补滤波器等算法来进一步优化姿态计算的精度和稳定性。

请注意，这只是一个简化的示例，实际应用中可能需要进行更多的校准、滤波和算法优化，以获得准确和稳定的姿态估计。同时，还需要考虑飞行器的动力学模型和控制算法，以实现自动控制和稳定飞行。

四元数

四元数是一种数学工具，用于表示旋转姿态。它是一个四维向量，包含一个实部和三个虚部。四元数的形式通常为q = w + xi + yj + zk，其中w是实部，(x, y, z)是虚部的三个分量。

四元数具有一些优点，使其在姿态表示和旋转计算中广泛应用：

1. 紧凑性：与欧拉角相比，四元数需要更少的存储空间和计算量来表示相同的旋转姿态。
2. 消除万向锁（Gimbal Lock）：在欧拉角表示中，当某个旋转轴与其他轴对齐时，会发生万向锁问题，导致旋转变得不可预测。而四元数表示可以避免万向锁问题，使旋转计算更稳定。
3. 插值和融合：四元数可以方便地进行插值和融合操作，用于平滑过渡和融合不同传感器的姿态信息。
4. 易于计算：四元数可以通过简单的乘法和加法运算来表示旋转操作，而不需要涉及复杂的三角函数运算，从而提高计算效率。

在飞行器自动控制中，常用的姿态表示方式之一是四元数。飞行器的姿态估计和控制算法可以使用四元数进行旋转计算、姿态插值和传感器融合。

需要注意的是，四元数的使用需要了解其代数运算规则和旋转转换方法。在实际应用中，可能需要使用四元数库或数学库提供的函数来进行四元数操作，以简化实现过程。

从MPU6050计算四元数

MPU6050是一个常用的惯性测量单元（IMU），它包含了加速度计和陀螺仪，但本身并不直接提供四元数的输出。然而，通过结合加速度计和陀螺仪的数据，并使用相应的算法，可以计算出四元数来表示飞行器的姿态。

以下是一个基于MPU6050的姿态计算示例，使用互补滤波器来计算四元数：

import math
from mpu6050 import MPU6050

# 初始化MPU6050传感器
mpu = MPU6050()

# 互补滤波器参数
accel_weight = 0.98
gyro_weight = 0.02

# 初始四元数
quaternion = [1.0, 0.0, 0.0, 0.0]

# 主循环
while True:
    # 读取加速度计和陀螺仪数据
    accel_data = mpu.get_acceleration()
    gyro_data = mpu.get_rotation()

    # 将加速度计数据转换为重力向量
    accel_vector = [accel_data['x'], accel_data['y'], accel_data['z']]
    accel_magnitude = math.sqrt(sum([a * a for a in accel_vector]))

    # 归一化加速度向量
    normalized_accel = [a / accel_magnitude for a in accel_vector]

    # 计算重力向量对应的四元数
    gravity_quaternion = [0.0, normalized_accel[0], normalized_accel[1], normalized_accel[2]]

    # 将陀螺仪数据转换为角速度向量
    gyro_vector = [gyro_data['x'], gyro_data['y'], gyro_data['z']]

    # 计算四元数的变化率
    delta_quaternion = [0.5 * dt * w for w in gyro_vector]

    # 更新四元数
    quaternion = [
        quaternion[0] + delta_quaternion[0],
        quaternion[1] + delta_quaternion[1],
        quaternion[2] + delta_quaternion[2],
        quaternion[3] + delta_quaternion[3]
    ]

    # 归一化四元数
    quaternion_magnitude = math.sqrt(sum([q * q for q in quaternion]))
    quaternion = [q / quaternion_magnitude for q in quaternion]

    # 使用互补滤波器融合加速度计和陀螺仪的姿态估计
    quaternion = [
        accel_weight * quaternion[i] + gyro_weight * gravity_quaternion[i]
        for i in range(4)
    ]

    # 输出四元数
    print("Quaternion: ", quaternion)

以上代码示例演示了如何从MPU6050读取加速度计和陀螺仪数据，并使用互补滤波器计算四元数来表示飞行器的姿态。注意，以上代码仅是一个“show me the code”的原理示例，实际应用中需要根据具体的编程环境和MPU6050库进行适当的调整。

公众号 | FunIO
微信搜一搜 “funio”，发现更多精彩内容。
个人博客 | blog.boringhex.top