＜数据结构＞NO7.二叉树(附Oj练习题)

news2024/11/27 8:44:35

 

 

         👇二叉树的完整代码在👇

syseptember的gitee仓库：二叉树https://gitee.com/syseptember/data-structure/tree/1513789167062c75dc172366199ce7a6b0577cc7/BinaryTree2/BinaryTree2

目录

树的概念及结构

0x01.树的概念

0x02.树的相关概念

0x03.树的表示

二叉树的概念及结构

0x01.二叉树的概念

0x02.特殊的二叉树

0x03.二叉树的性质

0x04.二叉树的结构

 二叉树的实现

0x01.构造二叉树

0x02.遍历二叉树

前中后序遍历

层序遍历

0x03.二叉树的高度与节点个数

🔨二叉树的节点个数

🔨二叉树的叶子节点个数

🔨二叉树第k层节点个数

🔨二叉树的高度

0x04.二叉树查找

🔨返回bool值

 🔨返回地址

0x05.判断是否为完全二叉树

二叉树的OJ练习

树的概念及结构

0x01.树的概念

📚定义： 树是一种非线性 的数据结构，它是由 n （ n>=0 ）个有限结点组成一个具有层次关系的集合。 把它叫做树是因 为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的

 📚性质：
①有一个特殊的节点，称为根节点。根节点没有前驱节点。
②除根节点外其余的节点被分成M(M>0)个互相不相交的节点T1、T2、T3......Tm，其中每一个集合Ti(1<=i<=m)都是不相交的集合。每一个集合又是与一棵树结构类似的子树。每棵子数的根节点都只有一个前驱，可以有0个或多个后继。
③树是递归定义的。
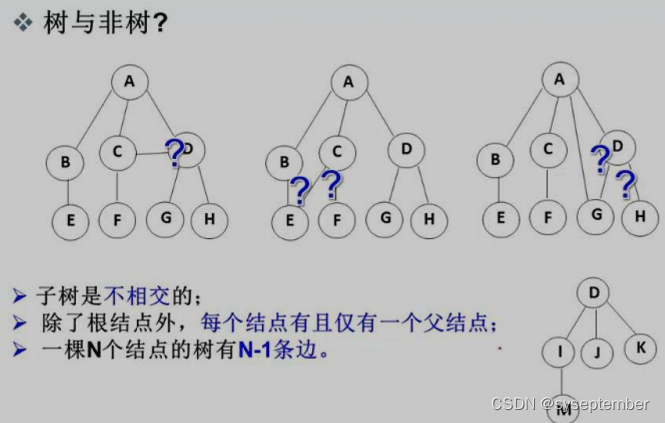
例如，下面的每一个框都可以看作上一个框的子树。

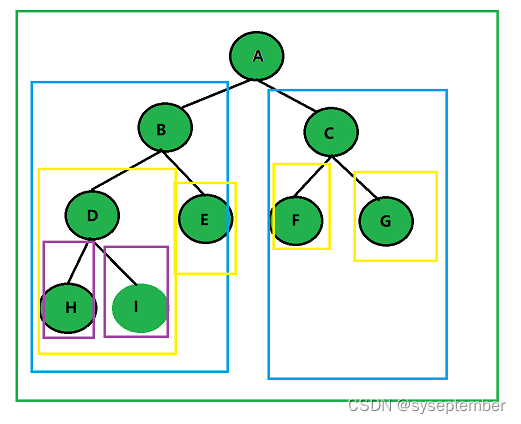
 ❗注意：在树形结构中，每一个集合(子树)不能有交集，否则就不是树了。

0x02.树的相关概念


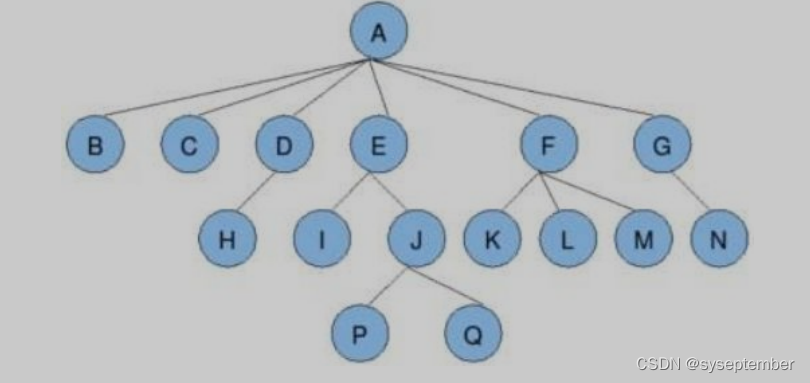
📚节点的度：一个节点含有子树的个数称为节点的度。上图中A的度是6.
📚叶节点(终端节点)：度为0的节点。上图中P、Q为叶子节点。
📚非终端节点(分支节点)：度不为0的节点。
📚子节点：一个节点含有的子树的根节点称为该节点的子节点。如上图BCDEFG是A的子节点。
📚父节点：父节点是一个相对概念，若一个节点含有子节点，那么称该节点为子节点的父节点。上图中A是BCDEFG的父节点。
📚兄弟节点：具有相同的父节点称为兄弟节点。如上图IJ是兄弟节点，JK不是兄弟节点。
📚树的度：一棵树中所有节点的最大度。如上图中树的度是6。
📚节点的层次：从跟根节点开始，根为第一层，根的子节点为第二层，以此类推。如上图中P的层次是4。
📚树的高度(深度)：树种节点的最大层次。如上图中树的高度是4。
📚堂兄弟节点：双亲在同一层的节点称为堂兄弟节点。如上图中J和K。
📚节点的祖先：从根节点到该节点所经分支上的的所有节点。如上图中M的祖先是A、F；Q的祖先是A、E、J。
📚子孙：以某节点为根的子树中的任意节点都称为该节点的子孙。如上图中所有节点都是A的子孙。
📚森林：由m（m>0）棵互不相交的树的集合称为森林。

📌对上面某些概念做出声明
①子节点和父节点的叫法不是固定的，也可以叫子女节点和母亲节点。
②节点的层次也可以将第一层的节点看作0层，第二层的节点看作1层，以此类推。

0x03.树的表示

        由于树不属于线性结构，所以在表示时既要将值存起来，还要将一个节点和其他多个节点的关系存储起来。数的表示方式有多种：双亲表示法、孩子表示法、孩子双亲表示法和孩子兄弟表示法；其中孩子兄弟表示法最常用，所以我们简单的了解下孩子兄弟表示法👇。

typedef int BTNodeDataType;
typedef struct BTnode
{
    struct BTNode* _pNextChild;//指向当前节点下一个孩子
    struct BTNode* _pFirsttBrother;//指向当前节点第一个兄弟节点
    BTNodeDataType vala;
}BTNode;

一个指针域指向下一个孩子节点，另一个指针域指向当前节点的第一个兄弟节点，每个节点这样链接就可以将整棵树连接起来。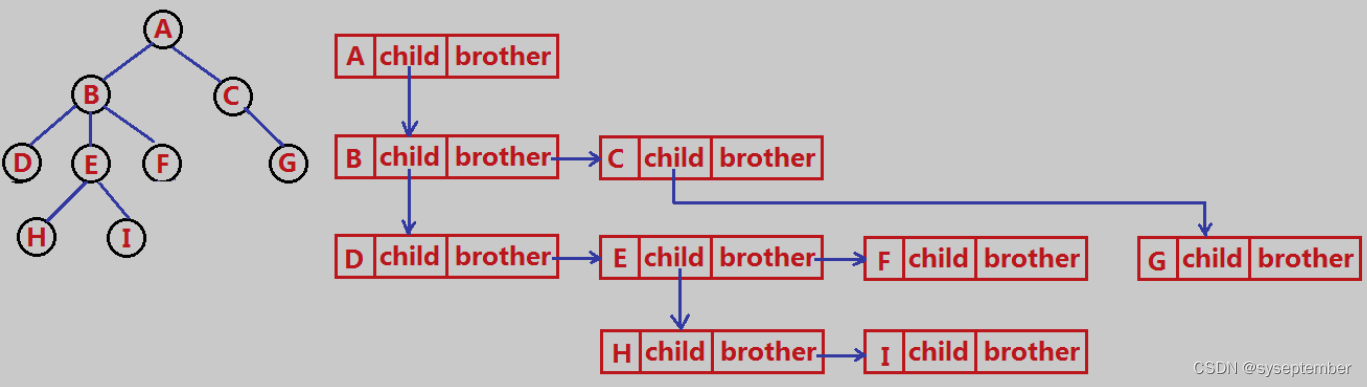

 📚树在文件系统中使用的较多。

二叉树的概念及结构

0x01.二叉树的概念

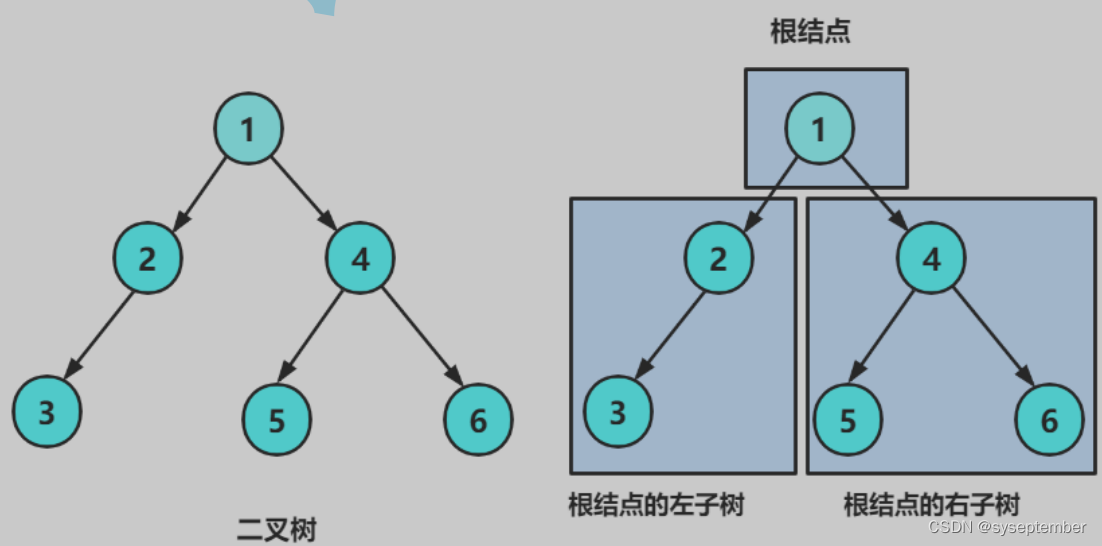
一棵二叉树是结点的一个有限集合，该集合:要么为空，要么由一个根节点个左右子树为二叉树的子树构成。
📚二叉树的特点：
①不存在度大于2的节点。
②二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树。

0x02.特殊的二叉树

1. 满二叉树
📚定义：除叶子节点外所有的节点都有2棵子树的二叉树称为满二叉树，满二叉树每一层的节点个数都达到了二叉树的最大值。满二叉树第k层的节点个数是2^(k-1)。

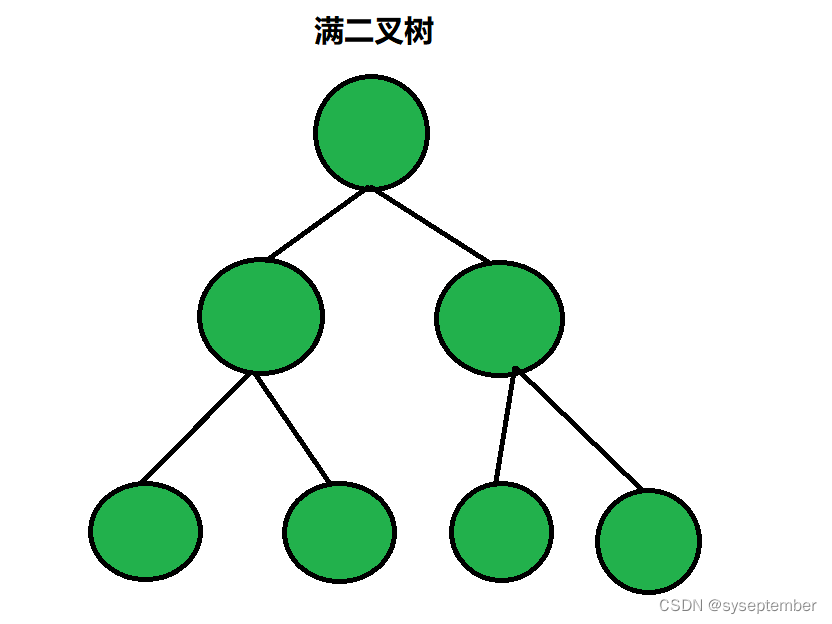
2. 完全二叉树 
📚定义：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的满二叉树的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。

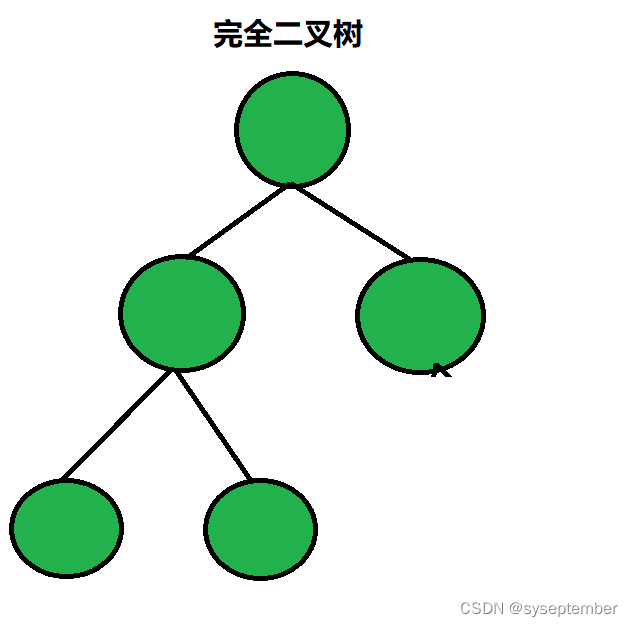
0x03.二叉树的性质

① 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1)个节点。
② 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h-1
③ 对任何一棵二叉树, 如果度为0其叶结点个数为n0,度为2的节点个数为n1,则n0=n1+1
④ 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=log(n+1)
⑤对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，对于序号为i的结点有：
1. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
2. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
3. 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

⑥对于完全二叉树，如果总结点树为奇数，那么没有度为1的节点；如果总结点数为偶数，则只有一个度为1的节点。

0x04.二叉树的结构

📚二叉树一般可以用链式结构或者顺序结构存储。

顺序存储
📚顺序存储就是使用数组进行存储，一般只会将完全二叉树用数组存储，因为不是完全二叉树时会有空间的浪费，而现实中，只有堆我们才会用数组存储，堆是一种特殊的完全二叉树。❗注意：使用数组存储时我们应该牢记：物理结构是数组，逻辑结构是二叉树。

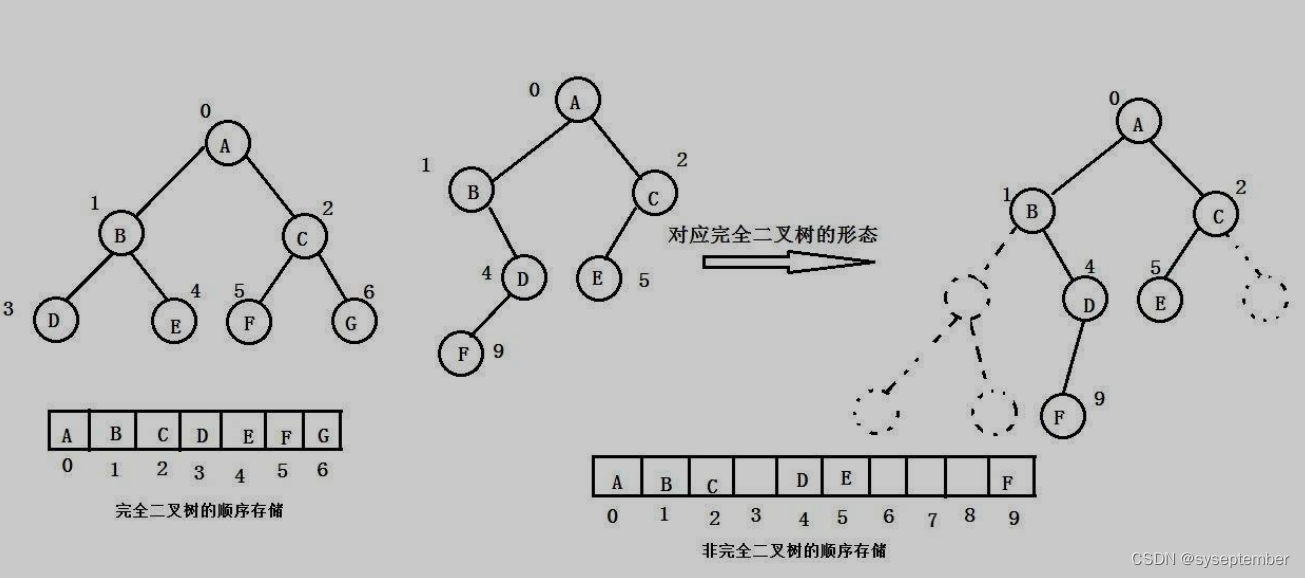
链式存储
📚二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。
📚通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。
📚链式结构又分为二叉链和三叉链，当前我们学习中一般都是二叉链，后面课程学到高阶数据结构如红黑树等会用到三叉链。


💬链式结构定义

//二叉链
typedef struct BinaryTwoTNode
{
	BTNodeDataType x;
	struct BinaryTwoTNode* left;
	struct BinaryTwoTNode* right;
}BT2Node;
//三叉链
typedef struct BinaryThreeNode
{
	BTNodeDataType x;
	struct BinaryThreeNode* _left;
	struct BinaryThreeNode* _right;
	struct BinaryThreeNode* _parent;
}BT3Node;

 二叉树的实现

只有完全二叉树中的堆才会采用顺序实现。可以移步到这篇文章👇syseptember的个人博客：堆的实现及应用http://t.csdn.cn/Squ6g

这里着重介绍二叉树的链式结构 。

0x01.构造二叉树

❗前置声明！！！

💭 在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二
叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树
操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

💬CreatBTree_Coding

BTNode* BuyOneNode(int x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	assert(node);
	node->left = node->right = NULL;
	node->x = x;
	return node;
}
BTNode* CreatBTree()
{
	BTNode* root = BuyOneNode(1);
	root->left = BuyOneNode(2);
	root->right = BuyOneNode(3);
	root->left->left = BuyOneNode(4);
	root->right->right = BuyOneNode(5);
	root->right->left = BuyOneNode(6);
	return root;
}

 上述构造的二叉树为

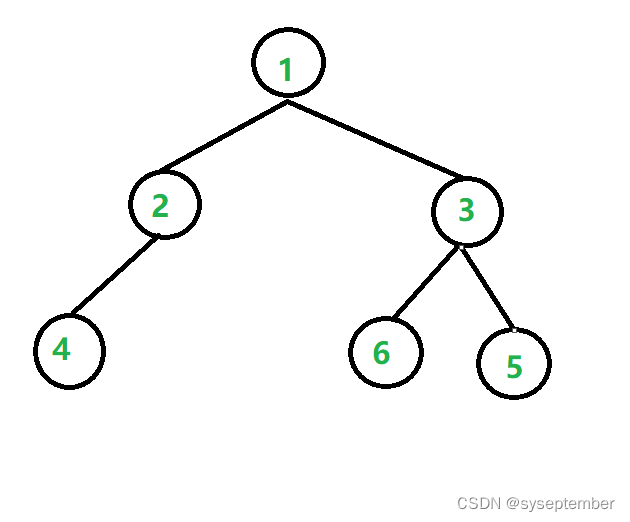
0x02.遍历二叉树

📚所谓遍历，就是按照某种特定的规则对二叉树节点进行访问，遍历二叉树是对二叉树最重要的操作之一，也是最基础的操作。二叉树的遍历有前序遍历、中序遍历、后序遍历、层序遍历。

前中后序遍历

 📚 前序遍历(Preorder Traversal 亦称先序遍历 )—— 访问根结点的操作发生在遍历其左右子树之前。
📚 中序遍历(Inorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之中（间）。
📚 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
由于被访问的结点必是某子树的根， 所以 N(Node ）、 L(Left subtree ）和 R(Right subtree ）又可解释为
根、根的左子树和根的右子树 。 NLR 、 LNR 和 LRN 分别又称为先根遍历、中根遍历和后根遍历。
 
🔨二叉树的前序遍历
前序遍历每次遍历一颗树时先便利这棵树的根，在遍历左子树，右子树，其中左子树也是按照先遍历左子树的根，再遍历左子树的左子树、左子树的右子树；右子树先便利右子树的根，在遍历右子树的左子树、右子树的右子树。也就是说每一棵树都要先便利根、左子树、右子树。所以上述前序遍历的顺序就是1-2-4-N-N-N-3-6-N-N-5-N-N
💬 PreOrder_Coding 
//前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N->");
		return;
	}
	//根
	printf("%d->", root->x);
	//左子树
	PreOrder(root->left);
	//右子树
	PreOrder(root->right);
}

代码很容易实现，难点是站在内存的角度去理解这段代码是如何执行的，这里画出它的递归展开可以更好的理解前序遍历👇

🔨二叉树的中序遍历
中序遍历每次先遍历左子树，再遍历根，最后遍历右子树，而左子树也是以中序的方式进行遍历。遍历上述树的结果是N-4-N-2-N-1-N-6-N-3-N-5-N
💬InOrder_Coding

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N->");
		return;
	}
	InOrder(root->left);
	printf("%d->", root->x);
	InOrder(root->right);
}

中序遍历和后续遍历类似，所以我们只画中序遍历的递归展开图👇

 🔨二叉树的后序遍历
后序遍历每次先遍历左子树，再遍历右子树，最后遍历根，而左子树、右子树也是以后序的方式进行遍历。后续遍历上述树结果是N-N-4-N-2-N-N-6-N-N-5-3-1
💬PostOrder_Coding

//后续遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N->");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d->", root->x);
}

后序遍历的递归展开图和中序类似，请大家自己完成。

层序遍历

📚 层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。
设二叉树的根节点所在层数为1 ，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第 2 层上的节点，接着是第三层的节点，以此类推， 自上而下，自左至右 逐层访问树的结点的过程就是层序遍历。
该二叉树的层序遍历结果就是1->2->3->4->5->6

 层序遍历不和子树的遍历有关因此层序遍历无法像前中后序一样使用递归。我们可以使用队列来对二叉树进行层序遍历。由于队列先进先出的特点，我们可以每次遍历一个节点时将它的左右子树的根节点入队。
🔨操作：例如遍历节点1时将2，3节点入队，遍历1后让1出队，接下来队列头就是2，遍历节点2时让4，5入队，遍历2后让2出队，此时队头变成3了......最先进来的是1，最先出去的也是1。

💬LevelOrder_Coding

//层序遍历
void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		QDataType front = QueueFront(&q);
		//队头出队前左右子树入队
		if (front->left)
			QueuePush(&q, front->left);
		if (front->right)
			QueuePush(&q, front->right);
		QueuePop(&q);
		printf("%d ", front->x);
	}
}

0x03.二叉树的高度与节点个数

💭前置声明：
在二叉树这一块，很多问题都可以通过层序遍历解决，但是个人认为的是二叉树更重要的是要掌握递归的思想以及理解递归，所以接下来的操作中即使可以用到层序遍历我也会使用递归，除非递归实在太复杂。

🔨二叉树的节点个数

❗注意：可以通过层序遍历求二叉树节点个数，也可以通过递归来求。只要掌握了层序遍历那么通过层序遍历求节点个数很容易，所以我这里只通过递归求二叉树的节点个数。

递归的2要素
①终止条件：当遍历到空节点是返回0，遍历到叶子节点时返回1。
②问题规模的缩小：将求二叉树节点问题转换为求左右子树节点个数之和，再用这个结果+1就是二叉树的节点个数。

💬BTreeSize_Coding

//获取节点个数
int BTreeSize(BTNode* root)
{
	//空节点返回0
	if (root == NULL)
		return 0;
	//叶子节点返回1
	if (root->left == NULL && root->right == NULL)
		return 1;
	return 1 + BTreeSize(root->left) + BTreeSize(root->right);
}

递归展开图：👇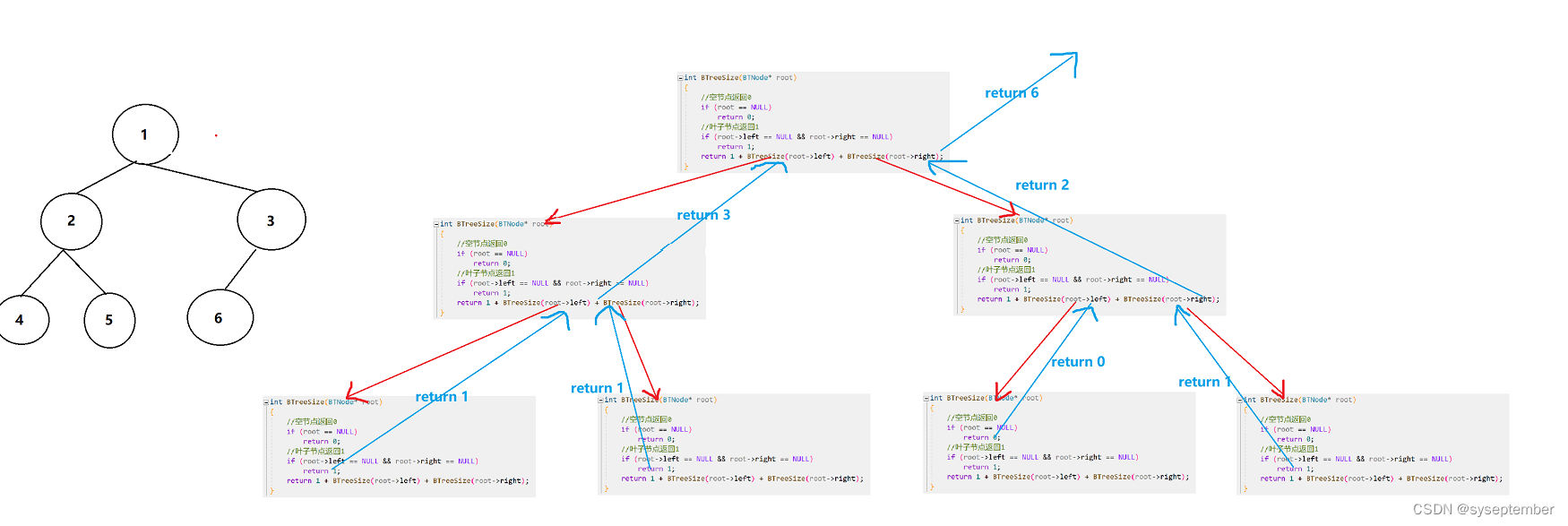

🔨二叉树的叶子节点个数

转换为递归问题
①终止条件：当遍历到空节点是返回0，遍历到叶子节点时返回1。
②问题规模的缩小：将求二叉树叶子节点问题转换为求左右子树叶子节点之和。

💬BTreeLeafSize_Coding

//获取叶子节点个数
int BTreeLeafSize(BTNode* root)
{
	//空节点返回0
	if (root == NULL)
		return 0;
	//叶子节点返回1
	if (root->left == NULL && root->right == NULL)
		return 1;
	//大问题化小
	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}

递归展开图：👇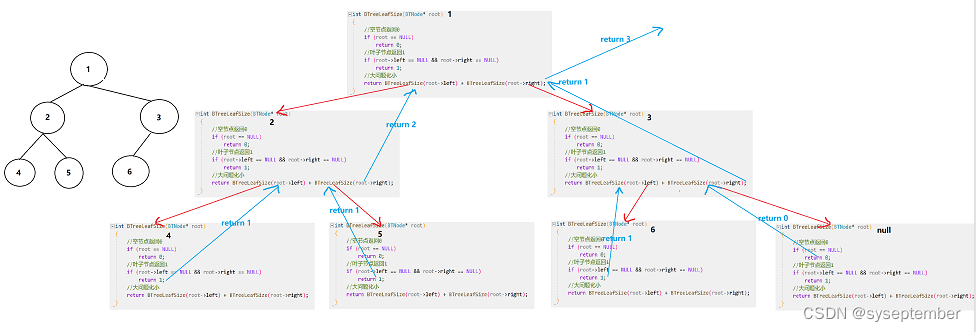

🔨二叉树第k层节点个数

转换为递归问题
①终止条件：当k==1时，返回1。当root==NULL时，返回0。
②问题规模的缩小：将求第k层节点转换为求左右子树第k-1层节点之和。

💬BTreeLevelSzie_Coding

//获取第k层节点个数
int BTreeLevelSize(BTNode* root, int k)
{
	//空节点不算个数
	if (root == NULL)
		return 0;
	//递归到了第k层
	if (k == 1)
		return 1;
	return BTreeLevelSize(root->left, k - 1) + BTreeLevelSize(root->right, k - 1);
}

递归展开图：👇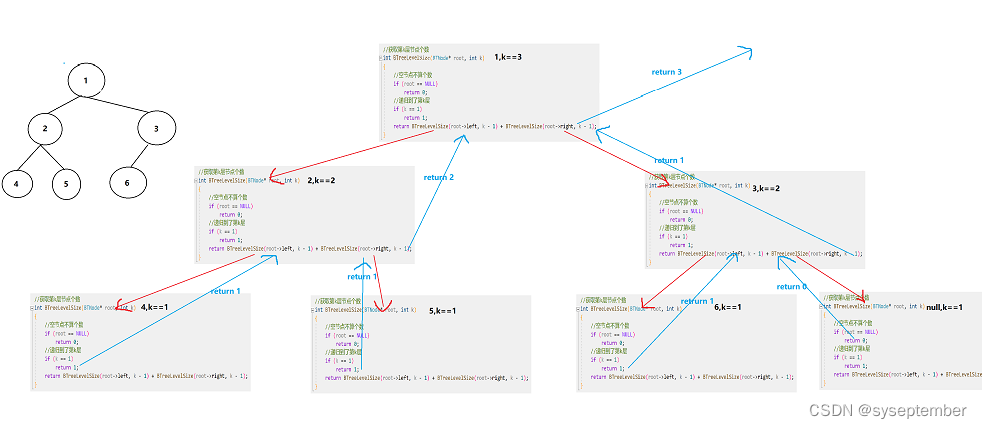

🔨二叉树的高度

转换为递归问题
①终止条件：遍历到空节点时返回0，遍历到叶子节点时返回1。
②问题规模的缩小：求二叉树的高度转换为求左子树的高度和右子树的高度，选出2个中较大的再+1就是二叉树的高度。

💬BTreeHeight_Coding

//求二叉树高度
int BTreeHeight(BTNode* root)
{
	//空节点不算高度
	if (root == NULL)
		return 0;
	//叶子节点算1层
	if (root->left == NULL && root->right == NULL)
		return 1;
	//每次将左右子树的高度存起来可以减少时间复杂度
	int ret1 = BTreeHeight(root->left) + 1;
	int ret2 = BTreeHeight(root->right) + 1;
	return ret1 > ret2 ? ret1 : ret2;
}

递归展开图：👇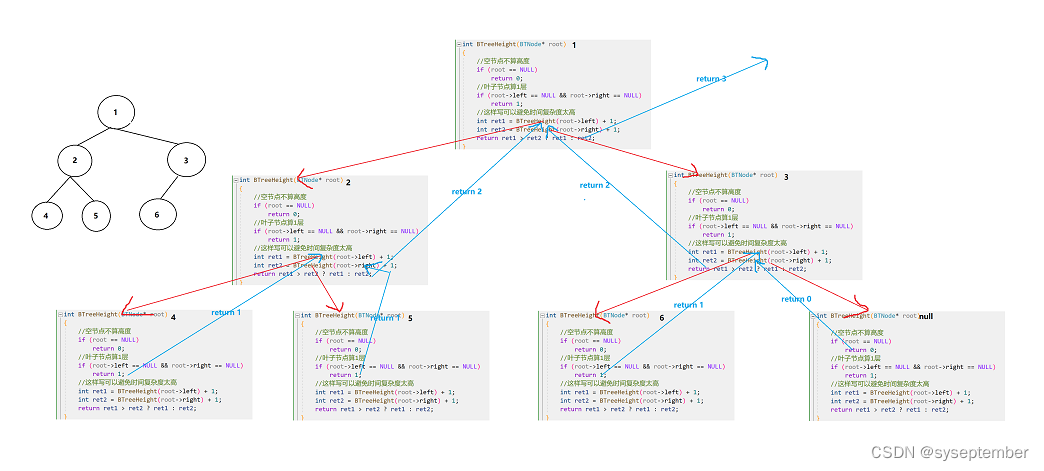

0x04.二叉树查找

💭前置声明：
由于普通二叉树的插入和删除没有意义，所以我们不实现普通二叉树的插入和删除，只实现查找，我们会对后续的avl树、红黑树才实现插入删除。

🔨返回bool值

在而二叉树中寻找一个数，找到返回true，没找到返回false。
用递归很容易实现
①终止条件：如果当前节点的值为寻找值，返回true，如果遍历到空节点，返回false。
②转换为子问题：在当前树查找转换为在左子树查找和在右子树查找，有一个找到即可。
💬BTreeFind_Coding

bool BTreeFind(BTNode* root, BTNodeDataType x)
{
	if (root == NULL)
		return false;
	if (root->x == x)
		return true;
	return BTreeFind(root->left, x) || BTreeFind(root->left, x);
}

递归展开图： 

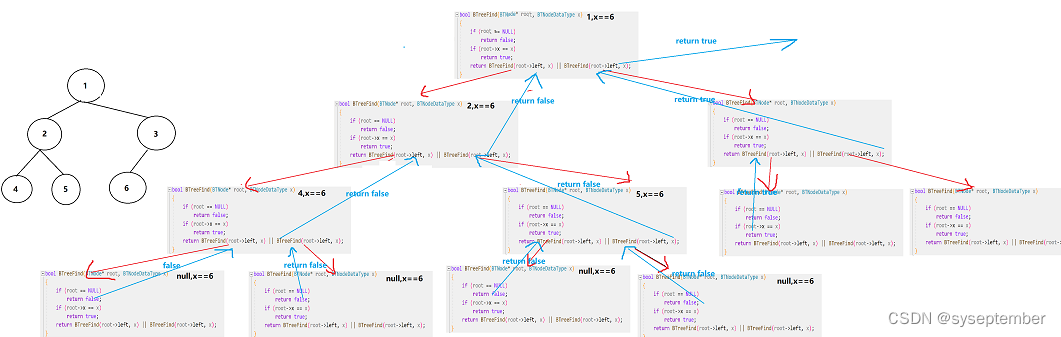
 🔨返回地址

现实中查找到了更多的是直接对该节点进行操作，因此我们需要返回节点的地址。

返回地址仍然可以使用递归求解
①终止条件：如果当前节点的值为寻找的值，返回该节点地址；如果该节点为空，返回NULL；
②转换为子问题：先在左子树找，如果没找到，再在右子树找，直接返回在右子树中找的结果。

💬BTreeFind_Coding

//寻找二叉树节点(返回地址)
BTNode* BTreeFind(BTNode* root, int x)
{
	if (root == NULL)
		return NULL;
	if (x == root->x)
		return root;
	BTNode* ret1 = BTreeFind(root->left, x);
	if (ret1 != NULL)
		return ret1;
	//左子树中没有找到目标节点
	BTNode* ret2 = BTreeFind(root->right, x);
	return ret2;
}

0x05.判断是否为完全二叉树

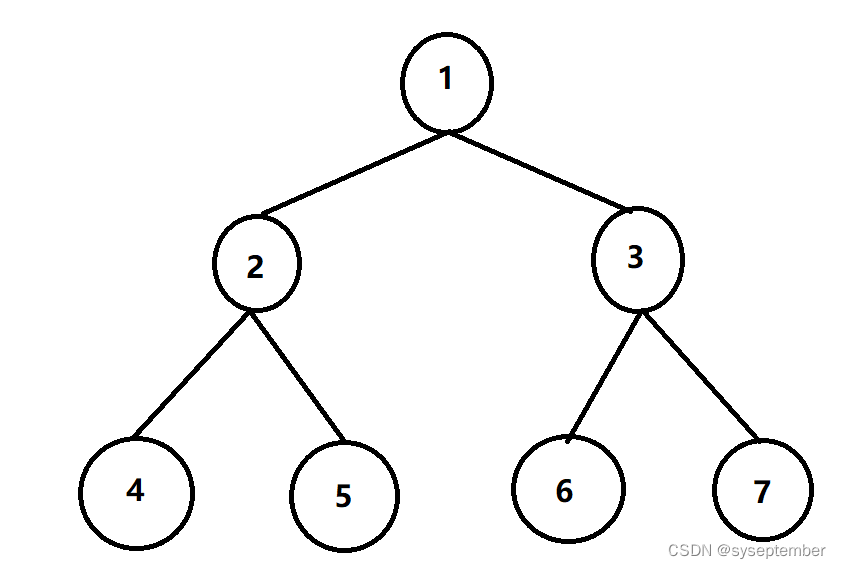
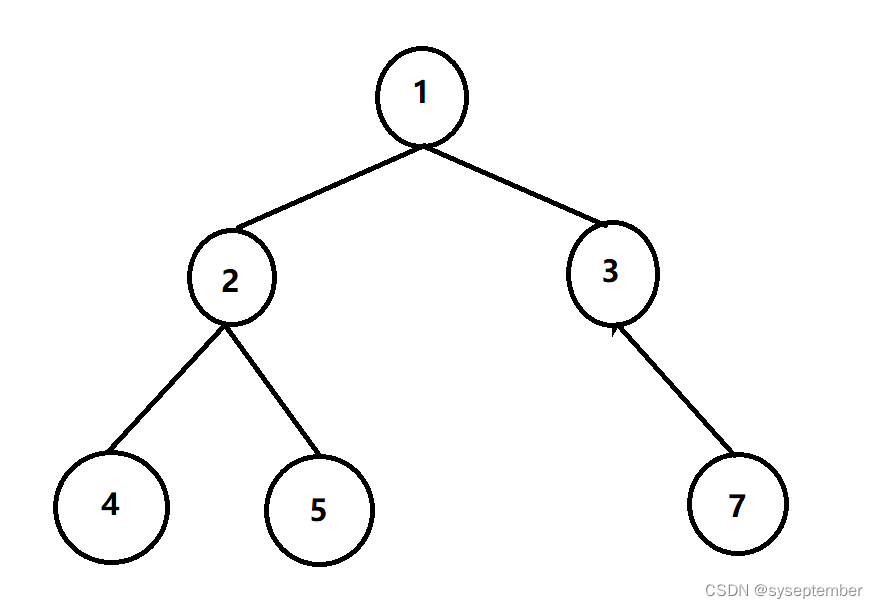
根据完全二叉树的形状可知：完全二叉树每一层的数据值都是连续的。因此可以使用队列判断是否为完全二叉树。下面是具体做法：
①构建一个队列，队列元素中存方树节点的地址。
②以层序遍历方式遍历树，直到入队元素为NULL，退出循环。
③继续遍历树中剩下的元素，若遍历到非空元素，说明第一个NULL元素后面出现了非NULL元素，说明不是完全二叉树，返回false。否则返回true。

💬isCompleteBTree_Coding

//判断是否为完全二叉树
bool isCompleteBTree(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);

	//找出队列中第一个值为空的元素
	while (QueueFront(&q) != NULL)
	{
		QDataType front = QueueFront(&q);
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
		QueuePop(&q);
	}

	while (!QueueEmpty(&q))
	{	//空元素不连续说明不是完全二叉树
		if (QueueFront(&q) != NULL)
			return false;
		QueuePop(&q);
	}
	return true;
}

二叉树的OJ练习

LeetCode965. 单值二叉树http://t.csdn.cn/sYvIaLeetCode100. 相同的树http://t.csdn.cn/eKmlMLeetCode101. 对称二叉树http://t.csdn.cn/8Hi06LeetCode144. 二叉树的前序遍历http://t.csdn.cn/SBYJsLeetCode572. 另一棵树的子树http://t.csdn.cn/VRdbFKY11 二叉树构建http://t.csdn.cn/WPyJc

LeetCode226. 翻转二叉树http://t.csdn.cn/pw1JvLeetCode110. 平衡二叉树http://t.csdn.cn/MznwT

👇二叉树的完整代码👇syseptember的gitee仓库：二叉树https://gitee.com/syseptember/data-structure/tree/1513789167062c75dc172366199ce7a6b0577cc7/BinaryTree2/BinaryTree2

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/607982.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

快速定位接口问题，JMeter方法论，跨线程组接口关联测试！

快速定位接口问题，JMeter方法论，跨线程组接口关联测试！

目录 【前言】 【步骤】 1. 准备工作 2. 创建线程组 3. 创建HTTP请求 4. 添加正则表达式提取器 5. 添加HTTP请求关联控制器 6. 设置断言和验证器 7. 运行测试 【代码】 【结论】 【前言】 在进行接口测试时&#xff0c;接口之间的关联经常是我们需要重点测试的点之…
阅读更多...
如何手写网络协议栈

如何手写网络协议栈

哈喽&#xff0c;我是子牙&#xff0c;一个很卷的硬核男人。喜欢研究底层&#xff0c;聚焦做那些大家想学没地方学的课程&#xff1a;手写操作系统、手写虚拟机、手写编程语言…目前做了两门课&#xff1a;手写OS、手写JVM 今天想跟大家聊一个黑科技&#xff1a;手写网络协议栈…
阅读更多...
Python的编码规范

Python的编码规范

目录 1、每个 import 语句只导入一个模块&#xff0c;尽量避免一次导入多个模块&#xff0c; 2、不要在行尾添加分号&#xff0c;也不要用分号将两条命令放在同一行&#xff0c; 3、建议每行不超过 80 个字符&#xff0c; 4、使用必要的空行可以增加代码的可读性 5、通常情…
阅读更多...
让百万大学生崩溃的在线OJ，如何破局？

让百万大学生崩溃的在线OJ，如何破局？

目录 一、在线OJ的的原理 二、在线OJ的使用规则 三、注意事项 1.关于作弊 2.如何防止作弊 3.输入输出格式 4.换行问题 四、经典在线OJ坑人题目以及博主被坑经历 五、提交不成功及解决方法 六、如何得心应手的拿下OJ系统 七、在线OJ的骗分技巧 在线OJ&#xff08;Onl…
阅读更多...
OpenGL简介

OpenGL简介

1.简介 一般它被认为是一个API&#xff0c;包含了一系列可以操作图形、图像的函数。然而&#xff0c;OpenGL本身并不是一个API&#xff0c;它仅仅是一个由Khronos组织制定并维护的规范(Specification)。OpenGL规范严格规定了每个函数该如何执行&#xff0c;以及它们的输出值。…
阅读更多...
为何要用分布式锁Redis实现分布式锁

为何要用分布式锁Redis实现分布式锁

为何要用分布式锁 一、为什么要使用分布式锁 为了保证一个方法在高并发情况下的同一时间只能被同一个线程执行&#xff0c;在传统单体应用单机部署的情况下&#xff0c;可以使用Java并发处理相关的API(如ReentrantLcok或synchronized)进行互斥控制。但是&#xff0c;随着业务…
阅读更多...
《论文阅读》连续前缀提示Prompt：table-to-text和摘要生成 ACL2021

《论文阅读》连续前缀提示Prompt：table-to-text和摘要生成 ACL2021

《论文阅读》连续前缀提示Prompt：table-to-text和摘要生成 ACL2021 前言相关知识Table-to-Text Generation自编码语言模型自回归语言模型简介任务定义部分参数更新代码实验结果前言 你是否也对于理解论文存在困惑？ 你是否也像我之前搜索论文解读，得到只是中文翻译的解读后…
阅读更多...
高级算法工程师的工作职责(合集）

高级算法工程师的工作职责(合集）

高级算法工程师的工作职责1 职责&#xff1a; 1、调研跟踪智能穿戴产品相关算法&#xff0c;为公司产品决策提供参考; 2、设计开发智能穿戴产品的计步、睡眠、心率、血氧饱和度、血压、心率变异性等相关参数的提取算法; 3、撰写算法开发文档&#xff0c;包括算法流程、测试方案…
阅读更多...
小黑西安归来，政审完毕，眼睛手术做完一直在家躺着第5天的leetcode之旅:852. 山脉数组的峰顶索引

小黑西安归来，政审完毕，眼睛手术做完一直在家躺着第5天的leetcode之旅:852. 山脉数组的峰顶索引

小黑代码 class Solution:def peakIndexInMountainArray(self, arr: List[int]) -> int:# 数组长度n len(arr)# 寻求山峰for i in range(n-1):if arr[i1] < arr[i]:return ireturn -1小黑二分模版 class Solution:def peakIndexInMountainArray(self, arr: List[int])…
阅读更多...
Linux——内存和DMA

Linux——内存和DMA

目录 本章目标&#xff1a; 一、内存组织 二、按页分配内存 三、slab分配器 四、不连续内存页分配 五、per-CPU变量 本章目标&#xff1a; 在前面的所有例子中&#xff0c;我们使用的都是全局变量或在栈上分配的内存。本章我们将先讨论如何动态分配内存和per-CPU变量。类…
阅读更多...
实战-k8s中部署tomcat（四）

实战-k8s中部署tomcat（四）

先下载资源&#xff1a;k8s中安装Tomcat 测试 k8s 集群中部署 tomcat 服务 #把 tomcat.tar.gz 上传到 k8s-node1&#xff0c;手动解压 [rootk8s-node1 ~]# ctr images import tomcat.tar.gz [rootk8s-master ~]# kubectl apply -f tomcat.yaml apiVersion: v1 #pod属于k8…
阅读更多...
Augmentation Matters：一种简单而有效的半监督语义分割方法(CVPR2023)

Augmentation Matters：一种简单而有效的半监督语义分割方法(CVPR2023)

文章目录 Augmentation Matters: A Simple-yet-Effective Approach to Semi-supervised Semantic Segmentation摘要本文方法Random Intensity-based AugmentationsAdaptive Label-aided CutMix 实验结果 Augmentation Matters: A Simple-yet-Effective Approach to Semi-superv…
阅读更多...
迅为RK3568开发板2800页手册+220集视频

迅为RK3568开发板2800页手册+220集视频

iTOP-3568开发板采用瑞芯微RK3568处理器&#xff0c;内部集成了四核64位Cortex-A55处理器。主频高达2.0Ghz&#xff0c;RK809动态调频。集成了双核心架构GPU&#xff0c;ARM G52 2EE、支持OpenGLES1.1/2.0/3.2OpenCL2.0、Vulkan 1.1、内高性能2D加速硬件。 内置NPU 内置独立NP…
阅读更多...
港联证券|AI概念股继续活跃 科创50指数逆势走高

港联证券|AI概念股继续活跃 科创50指数逆势走高

周三&#xff0c;A股市场出现极致分化态势。得益于存储芯片为代表的硬科技股的强势&#xff0c;科创50指数逆势走高。但创业板指、深证成指等主要股指仍然跌跌不休&#xff0c;沪指险守3200点关口。AI概念股继续逆势活跃&#xff0c;国资云、数据方向领涨&#xff0c;算力概念股…
阅读更多...
坂田杨美自然村旧改，已立项，直接签约。

坂田杨美自然村旧改，已立项，直接签约。

这个将由佳兆业与信义地产联合改造的坂田杨美自然村城市更新&#xff0c;已立项测绘&#xff0c;也公布了草案和村屋认定范围&#xff0c;正启动签约收楼中。名校附近的改造&#xff0c;深圳实验学校坂田校区附近&#xff0c;项目地处杨美地铁附近&#xff0c;还有佳兆业上品雅…
阅读更多...
【企业化架构部署】Nginx网站服务

【企业化架构部署】Nginx网站服务

文章目录 一、Nginx 概述1.什么是 Nginx2.Nginx 的特点3.Nginx 应用场景 二、Nginx 服务基础1.编译安装 Nginx 服务1.1 布置环境1.2 安装依赖包1.3 创建运行用户、组1.4 编译安装 2.Nginx 的运行控制2.1 检查配置文件2.2 启动、停止 Nginx2.3 日志分割以及升级 Nginx 服务2.4 添…
阅读更多...
39 KVM管理设备-管理快照

39 KVM管理设备-管理快照

文章目录 39 KVM管理设备-管理快照39.1 概述39.2 操作步骤 39 KVM管理设备-管理快照 39.1 概述 虚拟机在使用过程中可能由于病毒对系统的破坏、系统文件被误删除或误格式化等原因造成虚拟机系统损坏导致系统无法启动。为了使损坏的系统快速恢复&#xff0c;openEuler提供了存…
阅读更多...
每日学术速递5.30

每日学术速递5.30

CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.Accelerated Coordinate Encoding: Learning to Relocalize in Minutes using RGB and Poses(CVPR 2023 Highlight) 标题&#xff1a;加速坐标编码&#xff1a;学习使用 RGB 和姿势…
阅读更多...
阿里邮箱POP3/SMTP服务

阿里邮箱POP3/SMTP服务

最近发现一个问题&#xff0c;小伙伴给我发的邮件&#xff0c;收和回都不及时。于是我现在将所有的邮箱&#xff0c;通过POP3/SMTP协议整合到了一起。再配合小米手环&#xff0c;就能做到邮件无遗漏。 一、邮箱常用协议 邮箱中常用三类协议 POP3 Post Office Protocol versi…
阅读更多...
Python numpy - 数组与矩阵的运算

Python numpy - 数组与矩阵的运算

目录 数组array 一 数组的函数 unique函数 sum函数 max函数 二 数组的加减 三 数组的乘除 矩阵matrix 一 矩阵的生成 二 矩阵的加减 三 矩阵的乘法 数组array 创建数组a和b用来运算&#xff08;至少两个&#xff09; import numpy as np a np.random.randint(10,siz…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023