参考链接
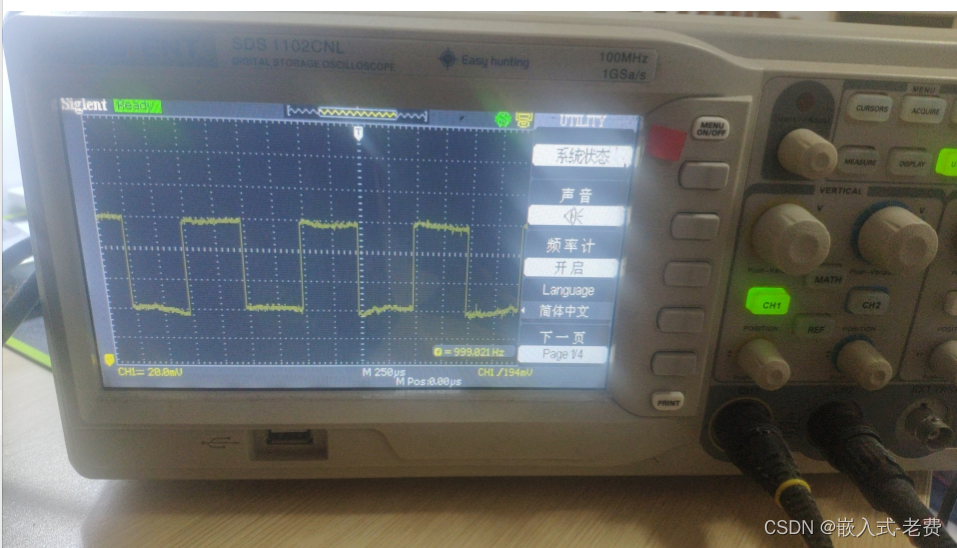
四倍空间的原因如上图所示,但是实际操作时,我们可以直接开三倍空间也是可以的。
原因分析:
由于在分割区间时,我们计算mid使用下取整,所以左边区间大小大于等于右边区间大小,如果要实现上图中的树,极端情况下实现最多的空节点,那么节点总数必然是
3
∗
2
k
3*2^k
3∗2k次方的形式,即所有次底层中每两个节点中有一个节点为叶子结点,也就是上图中的形式。
那么次底层的节点总数为
2
n
3
\frac{2n}{3}
32n,因为所有的叶子结点数为n。次底层中的一半才占据了三分之一的叶子结点。最底层所需的节点总数(包含空节点)为
4
n
3
\frac{4n}{3}
34n。由于空节点也是需要开辟空间,所以我们总需要的节点个数为
4
n
3
∗
2
−
1
\frac{4n}{3}*2-1
34n∗2−1。也就是
8
n
3
\frac{8n}{3}
38n,小于3n。
笔者亲测,洛谷线段树题目中使用
8
n
3
\frac{8n}{3}
38n,并不会产生段溢出。
线段树为什么可以开三倍空间
news2026/2/15 14:51:26
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/605513.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
智能路由器开发之创建一个procd init脚本示例
智能路由器开发之创建一个procd init脚本示例
Procd init脚本默认提供了许多好用的功能,例如重启策略和能够从UCI系统中存储和读取配置。
设置
举个例子,假设我们想创建一个作为服务的Shell脚本,并且这个服务可以通过消息和超时时间进行配…
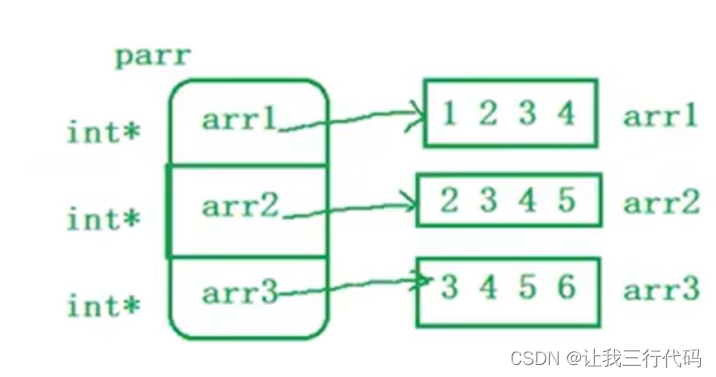
C语言---初识指针
1、指针是什么 指针是什么? 指针理解的2个要点: 1、指针是内存中一个最小单元的编号,也就是地址。 2、平时口语中说的指针,通常指的是指针变量,是用来存放内存地址的变量 总结:指针就是地址ÿ…
Docker+Jenkins+Gitee自动化部署maven项目,加入Nexus镜像仓库(补充篇)
1.前言
Hello,各位小伙伴,大家好!!!
在【DockerJenkinsGitee自动化部署maven项目】一文中,我们介绍了如何使用Jenkins来实现自动化部署maven项目,没读过的小伙伴可以去回顾一下,这…
【求 一个人去给多个人拜年 的最短路径】【枚举所有 拜访顺序】新年好
专注 效率 记忆 预习 笔记 复习 做题 欢迎观看我的博客,如有问题交流,欢迎评论区留言,一定尽快回复!(大家可以去看我的专栏,是所有文章的目录) 文章字体风格: 红色文字表示&#…
ChatGPT 70个插件小测全纪录
以下插件排序按照 ChatGPT all plugins 列表,评分基于国人使用场景。
1)Polarr:用于处理和编辑图片的工具 Polarr插件可以帮助用户进行各种图片编辑任务,包括调整亮度、对比度、饱和度,应用滤镜,裁剪图片,以及其他一些高级的图片处理功能。这个插件可以让ChatGPT更好地…
章节1:XXE漏洞-上
章节1:XXE漏洞-上
01 XML基础知识
XML
eXtensible Markup Language
可扩展标记语言
XML用途
配置文件 交换数据 XML内容 XML格式要求
XML文档必须有根元素XML文档必须有关闭标签XML标签对大小写敏感XML元素必须被正确的嵌套XML属性必须加引号
XML格式校验
…
耗时 48小时整理了网络安全学习路线,非常详细!
前言
上次发的文章【都2023年了,还在问网络安全怎么入门】很多小伙伴在评论区回复不知道怎么学习,我也反思了一下,确实没写到学习方法和路线,所以这一期就出一一个怎么学习网络安全的学习路线和方法,觉得有用的话三连…
mvn 打包jar包。 Docker 部署 jar 包程序
默认你已经安装了jdk和maven 并且配置了环境变量. 这里贴出自己的环境配置(mac)
# Maven3.6.3
export M2_HOME/Users/cc/maven3.6.3/apache-maven-3.6.3
export M2$M2_HOME/bin
export PATH$M2:$PATH# java8
export JAVA_HOME/Library/Java/JavaVirtualMachines/jdk1.8.0_36…
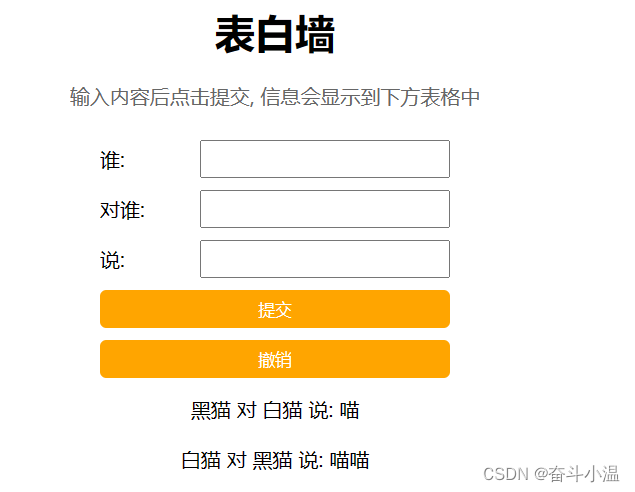
表白墙的实现【前后端交互】
目录
一、Servlet API 详解
1. HttpServletRequest
1.1 HttpServletRequest 方法
1.2 getParameter
2.HttpServletResponse
2.1 HttpServletResponse 方法
2.2 代码示例: 设置状态码
2.3 代码示例: 重定向
二、表白墙
1.准备工作 2.约定前后端交互接口
2.1 接口一…
项目引入Spring Security的参考步骤token
后端:
1、在数据库中创建t_user用户表,参照建表SQL。
2、pom文件中引入Spring Security依赖、JWT依赖(复制粘贴即可) <!--security--> <dependency> <groupId>org.springfr…
全志V3S嵌入式驱动开发(pwm驱动)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 pwm驱动也是常见的一种驱动方式。常见的pwm,其实就是一组方波,方波中的高低电平之比称之为空占比。通过调节这个空占比&…
前端学习--ES6模块化与异步编程高级用法
一、ES6模块化
1.1 概念与规则
ES6 模块化规范是浏览器端与服务器端通用的模块化开发规范 ES6 模块化规范中定义: 每个 js 文件都是一个独立的模块导入其它模块成员使用 import 关键字向外共享模块成员使用 export 关键字 1.2 在node.js体验es6模块化
配置如下&…
【问题】常见问题解决方法
记录在项目运行中遇到的问题,和常用的软件安装包 文章目录 安装包下载第一章:运行C/C小白运行须知1.DevC运行(最简单,推荐)2.Visual Studio 运行3.VC运行 第二章:运行C#项目1.VS环境2.打开C#项目启动失败&a…
LiteDram仿真验证(二):仿真中,DDR3初始化问题
目录 前言一、讨论1、[init_done never goes to 1 in simulation #145](https://github.com/enjoy-digital/litedram/issues/145)2、[Add ECP5 support to standalone core generator #106](https://github.com/enjoy-digital/litedram/issues/106)3、[Help generating DDR3 Ve…
【unity插件】2d切割破坏插件-Smart Slicer 2D
文章目录 效果1.切割2.破坏3.创建源码使用1.导入插件2.摄像机3.新建地面4.新建切割刀5.新建切割食物6. 运行即可不同slicer Type的切割刀类型测试1.线性2.Complex3.点4.多边形5.explode6.创建效果
1.切割
华为OD机试之数列描述(Java源码)
数列描述
题目描述 有一个数列a[N] (N60),从a[0]开始,每一项都是一个数字。数列中a[n1]都是a[n]的描述。其中a[0]1。规则如下: a[0]:1a[1]:11(含义:其前一项a[0]1是1个1,即“11”。表示a[0]从左到右,连续出…
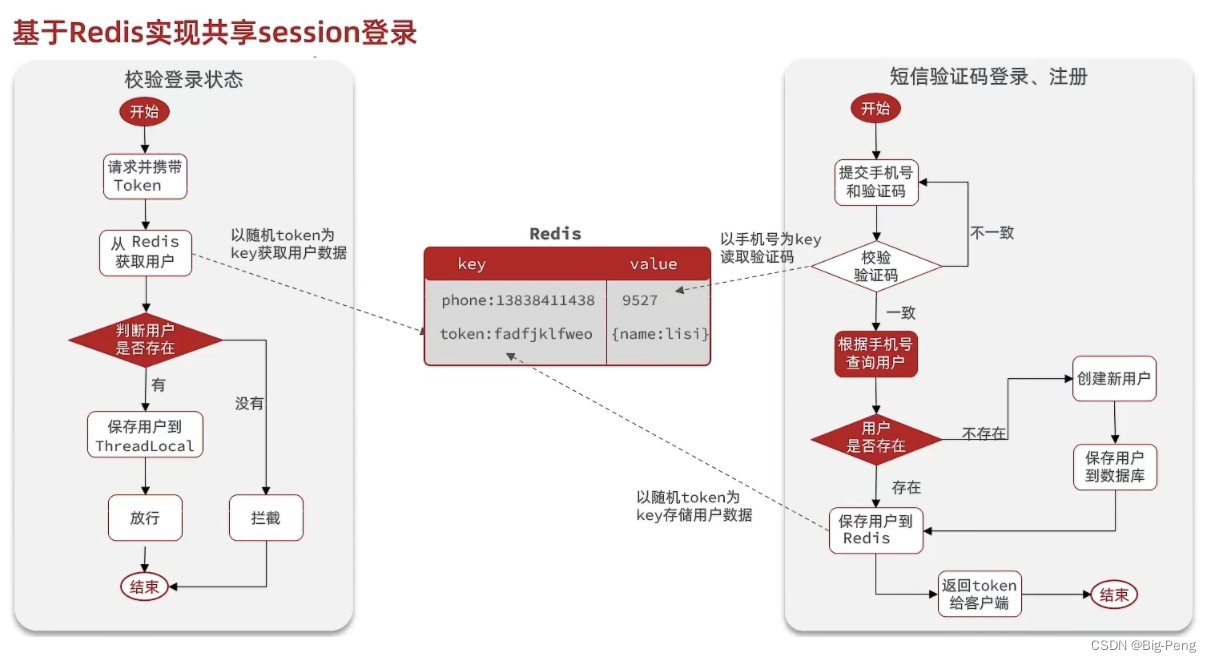
Java简单实现短信验证登录(Session、Redis)
前端设计
<div class"login-form"><div style"display: flex; justify-content: space-between"><el-input style"width: 60%" placeholder"请输入手机号" v-model"form.phone" ></el-input><e…
winform的RichTextBox控件追加文本及图片(实现笔记录入和笔记搜索功能)
在工作中,在工作中,难免有一些笔记要记录下来,方便后续工作中快速找到。之前用的是共享文档来记录的,但有一个缺点就是随着写的内容越来越多,打开变得很慢,搜索更加慢,网络不好的时候࿰…
Redis的常用数据结构之有序集合类型
有序集合的特点
集合中的元素有序,不可以重复与列表通过索引实现有序不同,有序集合实现有序的方式是通过给每一个集合元素设置一个分数score字段作为排序依据集合中的元素不能重复,但是score可以重复无法通过某一个下标的方式获取元素单个集…
大数据:spark环境搭建,local模式,standalone模式,zookeeper standby,yarn模式
大数据:spark环境搭建,local模式
2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,or…