1. 图论与算法

在计算机科学中，图论与算法是两个重要且紧密相关的领域。图论研究图的性质和特征，而算法设计和分析解决问题的方法和步骤。图论提供了一种形式化的方法来描述和分析各种关系和连接，而算法则为解决图相关的问题提供了有效的解决方案。

图论是研究图的结构和性质的学科。图是由节点（或顶点）和边组成的集合，节点代表实体，边表示节点之间的关系。图论涵盖了广泛的概念，包括图的类型（有向图和无向图）、路径、环、连通性、图的着色和匹配等。通过图论的研究，我们可以理解和分析复杂系统中的关系和交互。

算法是解决问题的一系列明确指令的有序集合。在图论中，算法的设计和分析旨在解决与图相关的问题，例如最短路径问题、最小生成树问题、最大流问题等。通过使用合适的算法，我们可以有效地解决这些问题，并找到最优的解决方案。在图论中，一些常用的算法包括深度优先搜索（DFS）、广度优先搜索（BFS）、迪杰斯特拉算法、克鲁斯卡尔算法和弗洛伊德算法等。

图论和算法在各个领域都有广泛的应用。在计算机网络中，图论帮助我们理解网络拓扑和路由问题，而算法则提供了寻找最短路径和最小成本路由的方法。在社交网络和推荐系统中，图论可以帮助我们分析用户之间的关系和交互，而算法可以为个性化推荐和社区发现提供支持。此外，图论和算法还在物流规划、电路设计、生物信息学和计算机视觉等领域中发挥重要作用。

2.图的表示

2.1 线性结构

线性数据结构： 线性数据结构不适合直接表示一般的图结构，因为线性数据结构是有序的，无法表达图中的节点之间的任意连接关系。线性数据结构如数组、链表等更适合表示树结构。

2.2 树结构

树结构： 树是一种特殊的图结构，具有层次性和无环的特点。树结构可以使用以下方式进行表示：

嵌套集合表示法（Nested Set Representation）：使用嵌套集合的方式来表示树，其中每个节点都具有一个范围（左右边界），可以方便地进行树的查询和遍历。

父节点指针表示法（Parent Pointer Representation）：每个节点存储一个指向其父节点的指针，通过这些指针可以沿着树的路径进行遍历。

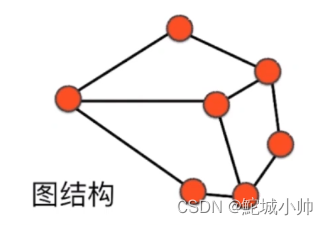
2.3 图结构

图结构： 图是由节点和边构成的一组连接关系，具有更复杂的结构。常见的图结构表示方法有以下几种：

• 邻接矩阵（Adjacency Matrix）：使用二维数组表示节点之间的连接关系，矩阵的行和列分别对应图的节点，矩阵元素表示边的存在与否。
• 邻接表（Adjacency List）：使用链表或数组的形式，为每个节点存储一个与之相邻的节点列表。每个节点的邻居节点可以通过遍历该列表来获取。
• 关联矩阵（Incidence Matrix）：使用二维数组表示节点和边的连接关系，矩阵的行对应节点，列对应边，矩阵元素表示节点和边之间的关联关系。

3. 图的遍历

图的遍历是指按照一定规则访问图中的所有节点。两种常见的图遍历算法是深度优先搜索（DFS）和广度优先搜索（BFS）。

• 深度优先搜索：从起始节点开始，沿着一条路径尽可能深入地访问图，直到到达末端节点或无法继续深入为止，然后回溯到上一个节点，继续探索其他路径。
• 广度优先搜索：从起始节点开始，先访问起始节点的所有邻居节点，然后依次访问邻居节点的邻居节点，直到图中的所有节点都被访问过为止。

3.1. 深度优先

深度优先搜索在图论中有多种应用：

（1）连通性：通过深度优先搜索可以确定图是否是连通的，即从一个节点出发是否可以到达图中的所有其他节点。

（2）路径：通过深度优先搜索可以找到两个节点之间的路径，或者判断是否存在一条路径连接两个节点。

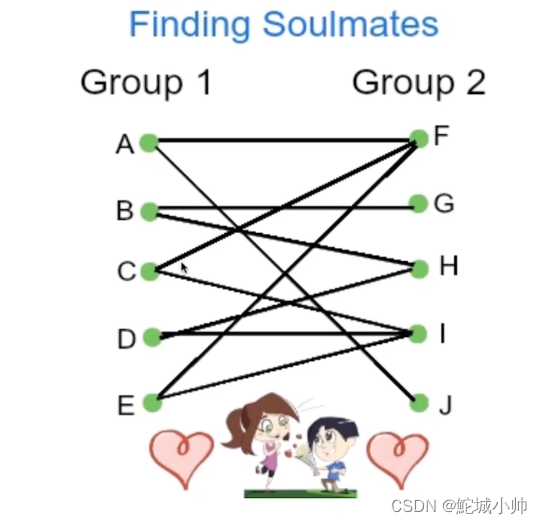
（3）二分图检测：通过深度优先搜索可以检测图是否是二分图，即是否可以将节点分成两个不相交的集合，使得每条边连接两个集合中的节点。

（4）环的检测：通过深度优先搜索可以检测图中是否存在环，即是否存在一条路径从某个节点出发回到该节点。

Floodfill：深度优先搜索可以用于填充连通区域，比如图像处理中的图像填充。

3.2. 广度优先

广度优先搜索在图论中的一个常见应用是求解无权图的最短路径问题。通过广度优先搜索，可以从起始节点开始逐层遍历，直到找到目标节点，从而找到起始节点到目标节点的最短路径。

4. 图论的应用

（1）网络分析：图论可以用于分析和理解社交网络、互联网、通信网络等各种网络结构。通过图论的算法和指标，可以研究网络中的节点关系、网络连通性、网络流量优化等问题。

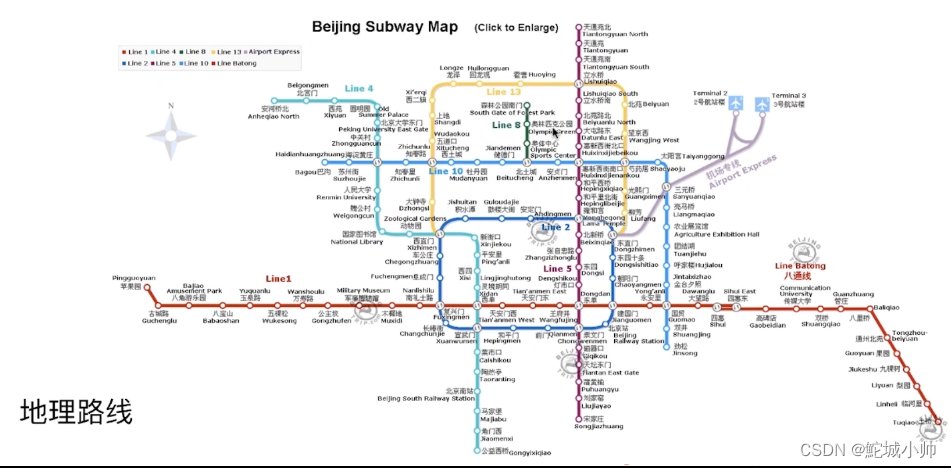
（2）路径规划：图论在路径规划领域中具有广泛应用。通过建模成图，可以使用最短路径算法来计算两个地点之间的最短路径，如导航系统中的路线规划。

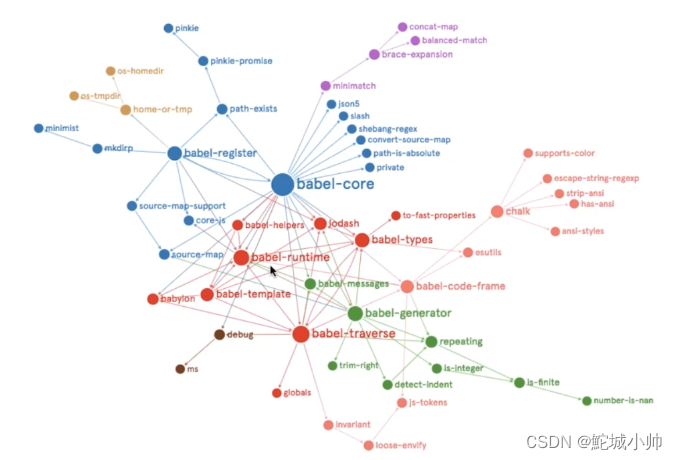
 （3）社交网络分析：图论可以用于研究社交网络中的社区结构、影响力传播、节点中心性等问题。通过分析图的拓扑结构和节点之间的关系，可以揭示社交网络的特征和动态。

（4）组合优化：图论在组合优化问题中发挥重要作用，如旅行商问题（TSP）、背包问题、分配问题等。通过将问题抽象为图，可以利用图论算法寻找最优解或近似最优解。

（5）数据聚类和分类：图论可以用于数据聚类和分类问题。通过将数据点表示为图的节点，根据节点之间的连接关系构建图，可以利用图的聚类算法对数据进行聚类和分类。

（6）生物信息学：图论在生物信息学中的应用很广泛，如基因组装、蛋白质相互作用网络分析、生物序列比对等。通过图论的方法，可以对生物学数据进行建模和分析。

（7）运筹学和优化问题：图论在运筹学和优化问题中有广泛应用，如资源分配、调度问题、流网络问题等。通过建立相关图模型，可以使用图论算法解决这些优化问题。

（8）计算机视觉：图论在计算机视觉领域中有着重要的应用，如图像分割、目标跟踪、图像匹配等。通过构建图模型，可以利用图论算法对图像数据进行处理和分析。

（9）论文引用分析：图论可用于研究学术文献中的引用关系，例如通过构建引用图，可以分析学术论文之间的引用网络结构、识别重要的论文和学术领域的研究热点。

（10）编译原理：图论在编译原理中也有重要应用，如语法分析和词法分析。通过构建语法分析树或词法分析自动机等图结构，可以实现程序的解析和编译。

（11）匹配问题：图论中的匹配算法可用于解决匹配问题，如稳定婚姻匹配问题、最大流量匹配问题等。这些算法可以为两个集合中的元素建立最佳的配对关系。